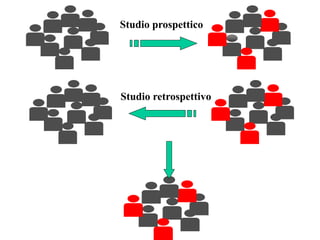
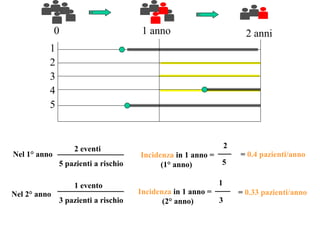
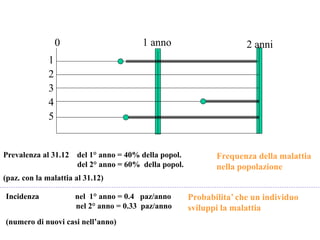
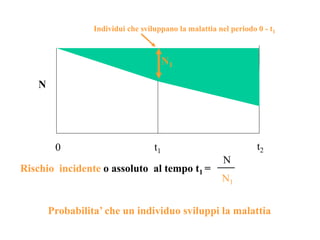
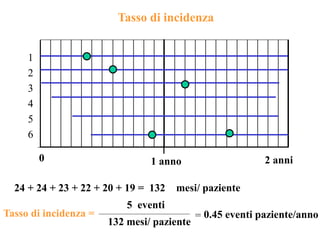
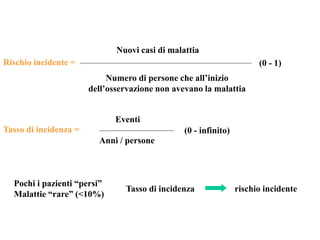
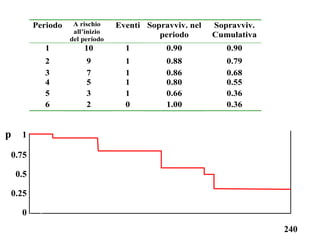
Il documento discute concetti chiave di epidemiologia e biostatistica, incluse misure di rischio come incidenza, prevalenza e tassi di mortalità. Viene presentato l'uso di metodi statistici come il test log-rank e analizzate le differenze tra studi prospettici e retrospettivi. Inoltre, sono incluse informazioni su tassi di mortalità e probabili correlazioni con fattori di rischio, con esempi applicati alla dialisi e a popolazioni specifiche.

1. IL RISCHIO
Concetti generali di epidemiologia e biostatistica
Tavole e curve di sopravvivenza
il metodo di Kaplan Meyer
il confronto fra curve (Log Rank test)
Il rischio misurato in base all’associazione di variabili categoriche
Studi prospettici: il rischio relativo
Studi retrospettivi: l’Odds ratio
Come si misura il rischio: le misure di frequenza
Prevalenza e incidenza
Rischio incidente
Tasso di incidenza
le misure d’impatto
Tasso di mortalita’

2. Studio prospettico
Studio retrospettivo

3. 0 1 anno 2 anni
Incidenza in 1 anno =
(1° anno)
2
5
Incidenza in 1 anno =
(2° anno)
1
3
1
2
3
4
5
Nel 1° anno
2 eventi
5 pazienti a rischio
Nel 2° anno
1 evento
3 pazienti a rischio
= 0.4 pazienti/anno
= 0.33 pazienti/anno

4. 1
2
3
4
5
Al 31.12 del 1° anno
2 casi
5 pazienti studiati
Prevalenza al 31.12 del 1° anno=
2
5
= 0.4
Al 31.12 del 2° anno
3 casi
5 pazienti studiati
Prevalenza al 31.12 del 2° anno=
3
5
= 0.6
0

5. 1
2
3
4
5
0 1 anno 2 anni
Frequenza della malattia
nella popolazione
Probabilita’ che un individuo
sviluppi la malattia
Prevalenza al 31.12 del 1° anno = 40% della popol.
del 2° anno = 60% della popol.
(paz. con la malattia al 31.12)
Incidenza nel 1° anno = 0.4 paz/anno
nel 2° anno = 0.33 paz/anno
(numero di nuovi casi nell’anno)

6. Registro Calabrese Dialisi 1995
Pazienti in dialisi al 31.12 1117
Abitanti 2.077.131
Prevalenza al 31.12 =1117/2,077 =537 dializzati per milione di abitanti
(0,5 ‰ o 0,05%)
Nuovi ingressi in dialisi 207
Incidenza nel 1995=207/2,077 =100 dializzati per milione ab. per anno
(0,1 ‰ o 0,01%)

7. 0 t1 t2
N
Individui che sviluppano la malattia nel periodo 0 - t1
N1
Rischio incidente o assoluto al tempo t1 =
N
N1
Probabilita’ che un individuo sviluppi la malattia

8. 0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
0 1 anno 2 anni
24 + 24 + 23 + 22 + 20 + 19 = 132 mesi/ paziente
Tasso di incidenza
Tasso di incidenza =
5 eventi
132 mesi/ paziente
= 0.45 eventi paziente/anno
1
2
3
4
5
6

9. Rischio incidente =
Tasso di incidenza =
Nuovi casi di malattia
Numero di persone che all’inizio
dell’osservazione non avevano la malattia
(0 - 1)
Eventi
Anni / persone
(0 - infinito)
Pochi i pazienti “persi”
Malattie “rare” (<10%)
Tasso di incidenza rischio incidente

10. IL RISCHIO
Concetti generali di epidemiologia e biostatistica
Tavole e curve di sopravvivenza
il metodo di Kaplan Meyer
il confronto fra curve (Log Rank test)
Il rischio misurato in base all’associazione di variabili categoriche
Studi prospettici: il rischio relativo
Studi retrospettivi: l’Odds ratio
Come si misura il rischio: le misure di frequenza
Prevalenza e incidenza
Rischio incidente
Tasso di incidenza
le misure d’impatto
Tasso di mortalita’

11. 1 anno
20 5 decessi in un anno 5/20
5
20
= tasso di mortalita’ annuale
Numero di decessi in un anno
popolazione totale
tasso di mortalita’ annuale =
(mortality rate)

12. 1995
40.125 pazienti in dialisi in Italia
Di 30.000 pazienti erano disponibili dati sulla mortalita’
2.123 pazienti erano deceduti nel 1995
Numero di decessi in un anno
popolazione totale
tasso di mortalita’ annuale =
(mortality rate)
2123 / 30000 = 0.707 0.707*100= 7.07
Numero di decessi
per cento pazienti / anno

13. tasso di mortalita’ annuale
6
20
= 0.3 = 3% paz./anno
deceduti Deceduti
per una
specifica causa
2
6
= 0.33 = 3.3%
paz. deceduti per una
specifica causa/anno
tasso di mortalita’ proporzionale
tasso di mortalita’ proporzionale =
(proportional mortality rate)
Numero di decessi per una
determinata causa
Numero totale di decessi

14. 1994 in Calabria:
Nella popolazione generale:
17.030 decessi 634 decessi per epatopatie
Fra i pazienti in dialisi:
105 decessi 10 decessi per epatopatie
tasso di mortalita’ proporzionale per epatopatie =
634
17.030
= 3.7 %
tasso di mortalita’ proporzionale per epatopatie =
10
105
= 9.5 %

15. 1994 in Calabria:
Nella popolazione generale:
Fra i pazienti in dialisi:
tasso di mortalita’ proporzionale per epatopatie
3.7 %
9.5 %
Il tasso di mortalita’ proporzionale, essendo
indipendente dalle dimensioni del campione,
consente di confrontare due popolazioni

16. Soggetti deceduti di eta’ compresa fra 65 e 75 anni
deceduti per epatopatia
Numero di pazienti deceduti
per epatopatia di eta’ 65-75
Numero di pazienti deceduti
di eta’ 65-75
6
20
=
tasso di mortalita’
specifico per eta’
(age specific mortality rate)
=

17. 1994 in Calabria :
Nella popolazione generale di eta’ 65 - 75:
4257 decessi 92 decessi per epatopatie
Fra i pazienti in dialisi di eta’ 65 -75:
76 decessi 6 decessi per epatopatie
tasso di mortalita’ specifico per eta’ =
92
4257
= 2.2 %
tasso di mortalita’ specifico per eta’ =
6
76
= 7.9 %

18. 1994 in Calabria:
Nella popolazione generale:
Fra i pazienti in dialisi:
tasso di mortalita’ proporzionale per epatopatie
3.7 %
9.5 %
Nella popolazione generale:
Fra i pazienti in dialisi:
tasso di mortalita’ per epatopatie specifico per eta’ (65 - 75)
2.2 %
7.9 %

19. IL RISCHIO
Concetti generali di epidemiologia e biostatistica
Tavole e curve di sopravvivenza
il metodo di Kaplan Meyer
il confronto fra curve (Log Rank test)
Il rischio misurato in base all’associazione di variabili categoriche
Studi prospettici: il rischio relativo
Studi retrospettivi: l’Odds ratio
Come si misura il rischio: le misure di frequenza
Prevalenza e incidenza
Rischio incidente
Tasso di incidenza
le misure d’impatto
Tasso di mortalita’

20. Fumatori
Non fumatori
Evento
Non evento
Fumatori Non fumatori
5 3
7 9
Rischio incidente= 5/12 3/12

21. Evento
Non evento
Fumatori Non fumatori
5 3
7 9
Rischio incidente= 5/12 3/12
(0.42) (0.25)
Presente Assente
A B
C D
Fattore di rischio
sfavorevole
Esito
favorevole
RR=
A:(A+C)
B:(B+D)
Rischio relativo (RR)=
0.42
0.25
= 1.68

22. Fattore di rischio:presente
?
?
Evento
Non ev.
Evento.
Non ev.
Odds 5/3 7/9
(1.66) (0.77)
Fattore di rischio:assente
Evento
Non evento
Presente Assente
5 3
7 9
Fattore di rischio

23. Odds ratio =
A : B
C : D
Evento
Non evento
Presente Assente
5 3
7 9
Fattore di rischio
Odds 5/3 7/9
(1.66) (0.77)
Odds Ratio (OR) =
1.66
0.77
= 2.15
Evento
Non evento
Presente Assente
A B
C D
Fattore di rischio
Odds A/B C/D
Rischio Relativo =
A:(A+C)
B:(B+D)
Eventi Rari
A e B 0
A : B
C: D
= Odds ratio

24. Rischio Relativo = 1
Rischio Relativo > 1
=
>

25. CI -90% CI +90%1
RR
-2 -1 0 1 2 3

26. CI -90% CI +90%
RR
-2 -1 0 1 2 3

27. IL RISCHIO
Concetti generali di epidemiologia e biostatistica
Tavole e curve di sopravvivenza
il metodo di Kaplan Meyer
il confronto fra curve (Log Rank test)
Il rischio misurato in base all’associazione di variabili categoriche
Studi prospettici: il rischio relativo
Studi retrospettivi: l’Odds ratio
Come si misura il rischio: le misure di frequenza
Prevalenza e incidenza
Rischio incidente
Tasso di incidenza
le misure d’impatto
Tasso di mortalita’

28. Rischio incidente
Tavole (curve) di sopravvivenza: Kaplan Meyer

29. 1
2
3
4
5
6
7
8
9
10
40 59 122 163 1720 240 giorni
= Evento
= Censurati (persi, deceduti per altre cause,
viventi alla fine dell’osservazione)
RI =
Eventi (nel periodo)
Pazienti all’inizio del periodo
Probabilita’ di sopravvivenza = 1-RI
RI =
1
10
= 0.1 (10%)
Ps1 = 1 -
1
10
= 0.9 (90%)

30. RI =
Eventi (nel periodo)
Pazienti all’inizio del periodo
Probabilita’ di sopravvivenza = 1-RI
RI =
1
10
= 0.1 (10%)
Ps1 = 1 -
1
10
= 0.9 (90%)
Probabilita’ di sopravvivenza = 1 -
(in ogni periodo)
Eventi (nel periodo)
Pazienti all’inizio del periodo

31. 1
2
3
4
5
6
7
8
9
10
40 59 122 163 1720 240 giorni
Periodo A rischio
all’inizio
del periodo
Eventi Sopravviv. nel
periodo
Sopravviv.
Cumulativa
1 10 1 0.90 0.90
2 9 1 0.88 0.79
3 7 1 0.86 0.68
4 5 1 0.80 0.55
5 3 1 0.66 0.36
6 2 0 1.00 0.36
1-(eventi/a rischio all’inizio del periodo)
Periodo A rischio
all’inizio
del periodo
Eventi Sopravviv. nel
periodo
Sopravviv.
Cumulativa
1 10 1 0.90 0.90
2 9 1 0.88 0.79
3 7 1 0.86 0.68
4 5 1 0.80 0.55
5 3 1 0.66 0.36
6 2 0 1.00 0.36
Periodo A rischio
all’inizio
del periodo
Eventi Sopravviv. nel
periodo
Sopravviv.
Cumulativa
1 10 1 0.90 0.90
2 9 1 0.88 0.79
3 7 1 0.86 0.68
4 5 1 0.80 0.55
5 3 1 0.66 0.36
6 2 0 1.00 0.36

32. p 1
0.75
0.5
0.25
0
40 59 122 163 172 240
Periodo A rischio
all’inizio
del periodo
Eventi Sopravviv. nel
periodo
Sopravviv.
Cumulativa
1 10 1 0.90 0.90
2 9 1 0.88 0.79
3 7 1 0.86 0.68
4 5 1 0.80 0.55
5 3 1 0.66 0.36
6 2 0 1.00 0.36

33. p 1
0.75
0.5
0.25
0
240
O1 = Eventi osservati nel 1° gruppo A1= Eventi attesi nel 1° gruppo
O2 = Eventi osservati nel 2° gruppo A2 = Eventi attesi nel 2° gruppo
Log Rank X2 = +
(O1 - A1)2
A1
(O2 - A2)2
A2