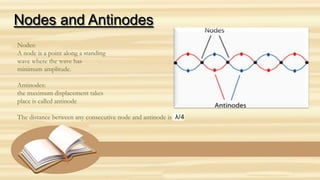
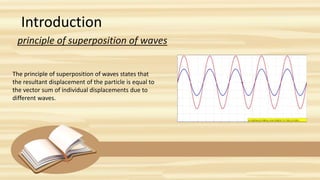
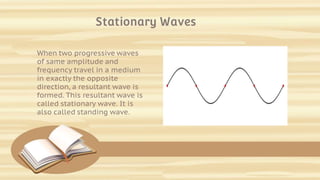
This document discusses the principle of superposition of waves and the formation of stationary waves. It defines superposition of waves as the vector sum of individual displacements from different waves. There are two types of interference - constructive and destructive - depending on whether the waves are in phase or out of phase. A stationary wave is formed when two progressive waves of the same amplitude and wavelength travel in opposite directions. The stationary wave has nodes where the amplitude is minimum and antinodes where it is maximum.

1. Application of principle of
superposition of wave in the
formation of stationary wave

2. Presented by : [SECTION M2] Yukesh Gautam
Sirson Sharma
Ujjwal Shah
Shreeyansh Poudel
Sarthak Rijal

3. ACKNOWLEDGEMENT :
Never let small minds convince you that your dreams are too big!!
Hello and good morning to you all from my side. I Yukesh Gautam on the behalf of my
team members would like to express the deep sense of gratitude to our Uniglobe college
and respected teacher Mr. Saroj Baral who gave the
golden opportunity to do this project. I really acknowledge your support ,effort and timely
guidance which actually helped us in better understanding of the subject matter.
Also,
I could not forget my team members who have been so instrumental in the preparation of the project.
It was totally impossible to finalize the project without you!! Really kind effort and encouragement.

4. TABLE OF CONTENT
 Introduction
 Types of superposition waves
 Stationary waves
 Nodes and antinodes
 Characteristics
 Conclusion

5. The principle of superposition of waves states that
the resultant displacement of the particle is equal to
the vector sum of individual displacements due to
different waves.
Introduction
principle of superposition of waves

6. If y be the resultant displacement of a
particle and y1, y2, . . . are displacements
due to individual waves, then according to
the principle of
superposition of waves, we have
y= y1 + y2 + y3… +yn

7. Superposition of wave
Interference
There are two types of interference of a wave.
i. Constructive interference
ii. Destructive interference

8. CONSTRUCTIVE
INTERFERENCE
If two waves superimposed with
each other in the same phase,
the amplitude of the resultant is
equal to the sum of the
amplitudes of individual waves
resulting in the maximum
intensity of light, this is known
as constructive interference

9. Destructive
Interference
If two waves superimpose
with each other in opposite
phase, the amplitude of the
resultant is equal to the
difference in amplitude of
individual waves, resulting in
the minimum intensity of
light, this is known as
destructive interference.

11. Let y1 and y2 be the displacements of
two progressive waves of same
amplitude a and wave length
travelling in opposite direction
simultaneously with the same velocity v.
The equations of these waves may be
expressed as follows,
y1 = a sin (ωt – kx) . . . (1)
y2 = a sin (ωt + kx) . . . (2)
Thus, the resultant displacement of the
particle of medium due to both the
waves will be determined

12. from the principle of superposition,
= y1 + y2
= a sin (ωt – kx) + a sin (ωt + kx)
= a [sin (ωt – kx) + a sin (ωt + kx)] Applying formula sinC+sinD
y = 2a cos kx. sinωt
y = A sinωt . . . (3)
Equation (3) represents a simple harmonic wave whose amplitude is A = 2a
cos kx. It is evident that, for different values of x, the amplitude will have
different values. Obviously, the frequency of stationary wave is equal to the
interfering waves i.e. there is no change in frequency.

13. Nodes and Antinodes
Nodes:
A node is a point along a standing
wave where the wave has
minimum amplitude.
Antinodes:
the maximum displacement takes
place is called antinode
The distance between any consecutive node and antinode is λ/4

14. 1) One easy to understand example is two people shaking either end of a jump rope.
If they shake in sync, the rope will form a regular pattern with nodes and antinodes
and appear to be stationary, hence the name standing wave.
2) When we press a guitar string against the fret, we are fixing one of the ends, thus
causing a reflection phenomenon: when a wave formed in the string reaches the fret,
it is reflected and travels backwards.

15. CONCLUSION :
Overall, this project is the
source of knowledge of
Superposition of wave
and its types.
Again I will like to thanks
our respected teacher Mr
Saroj Baral for gaving us
golden opportunity to
participate in this project.