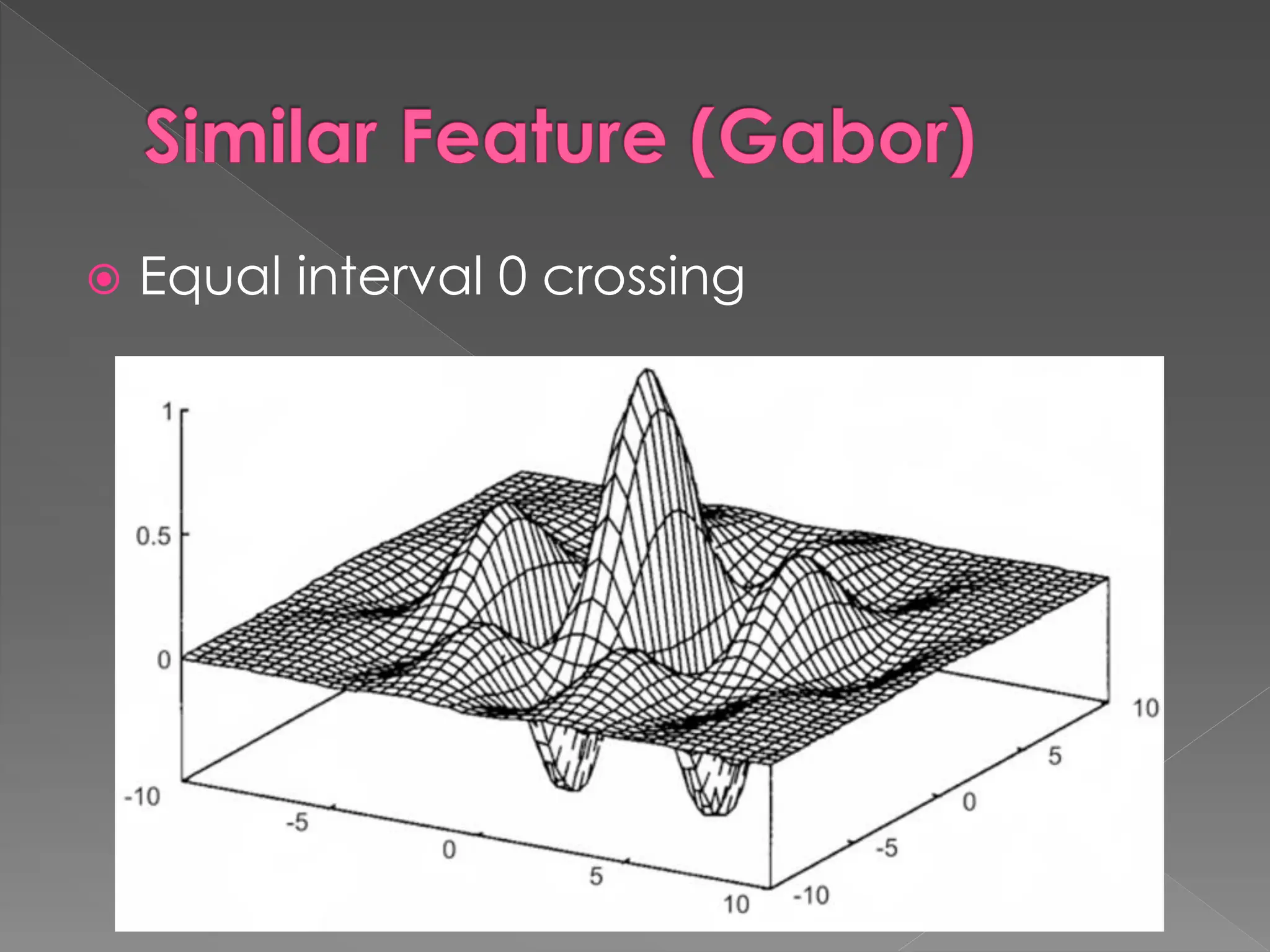
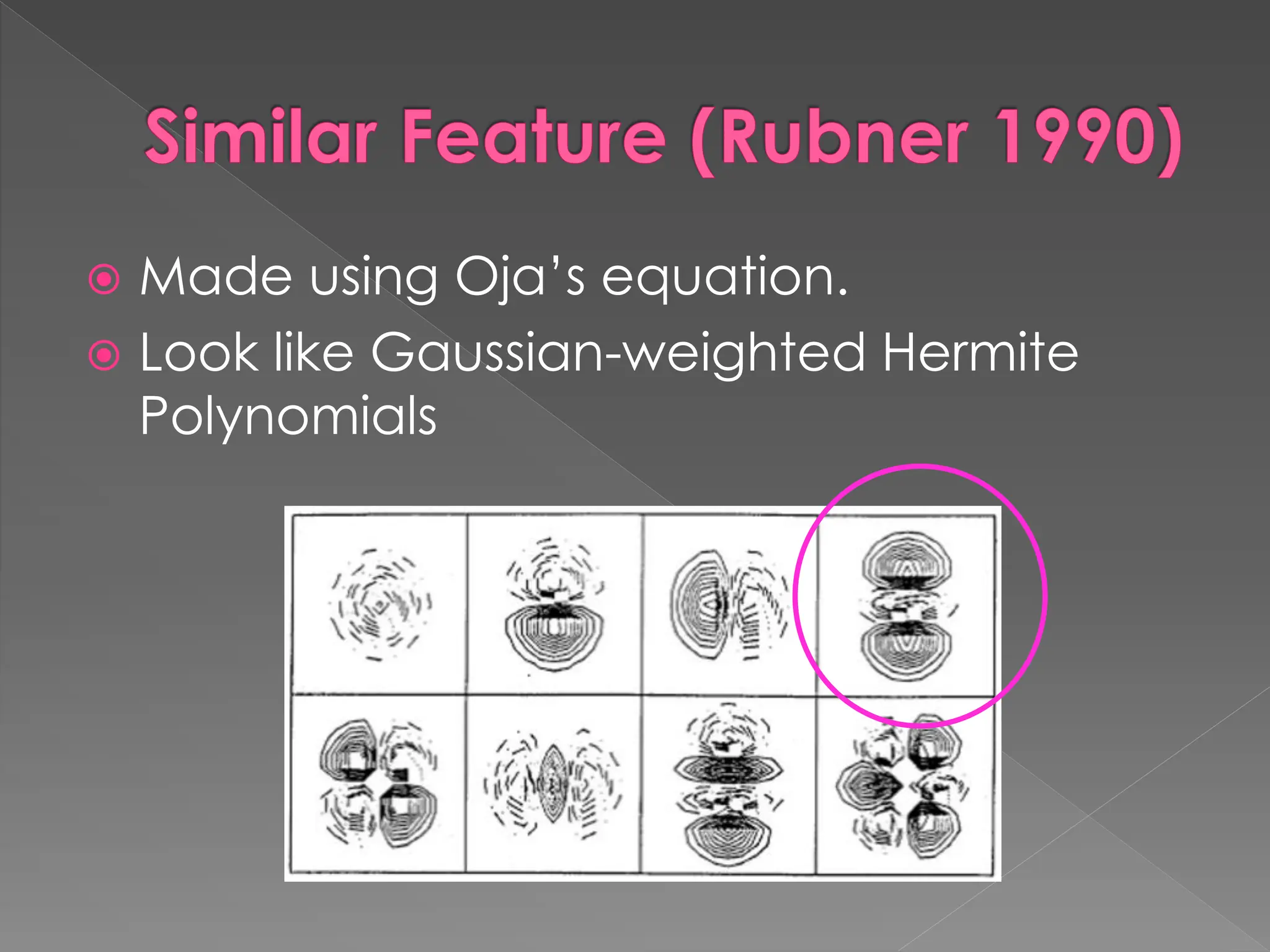
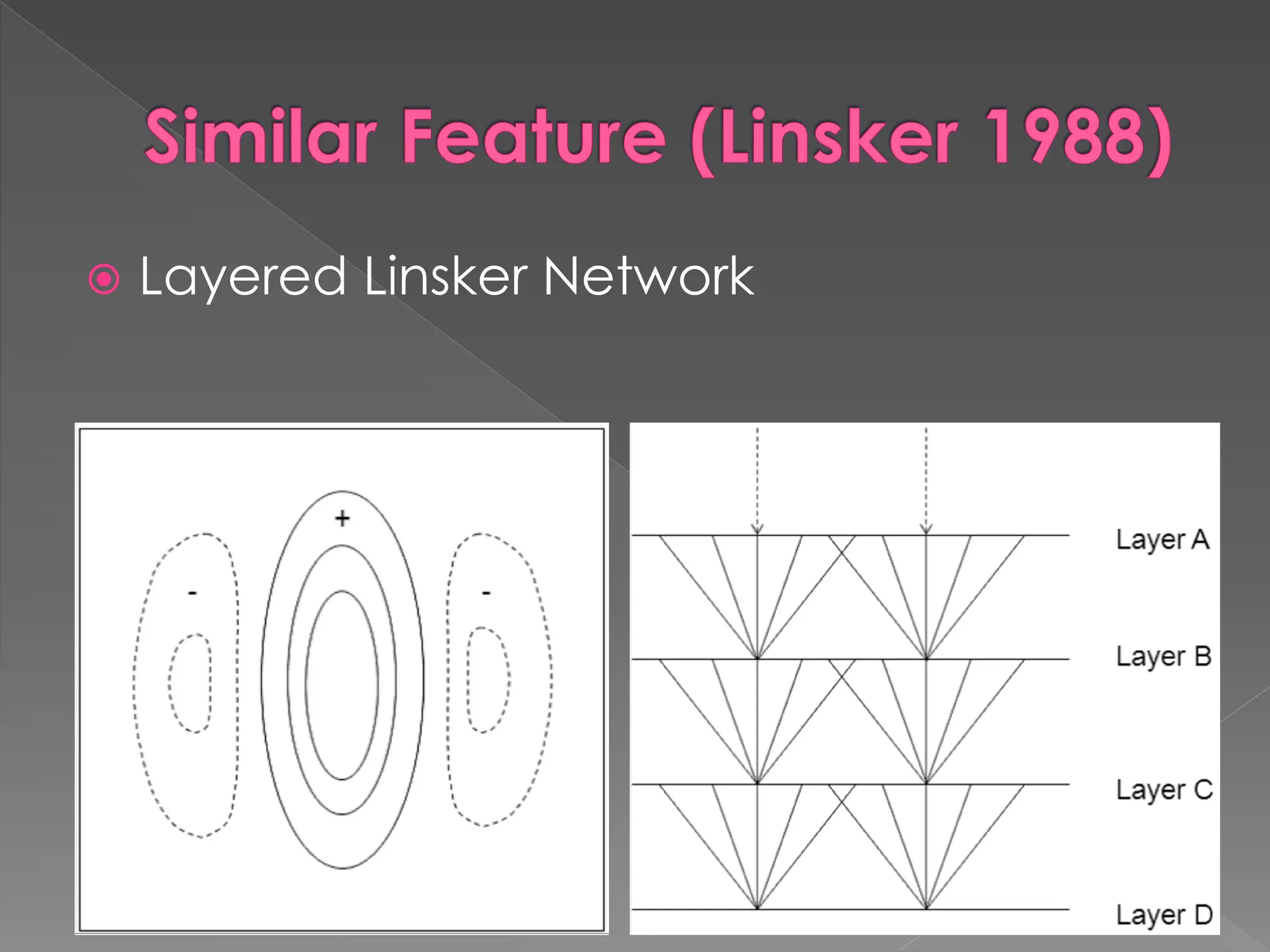
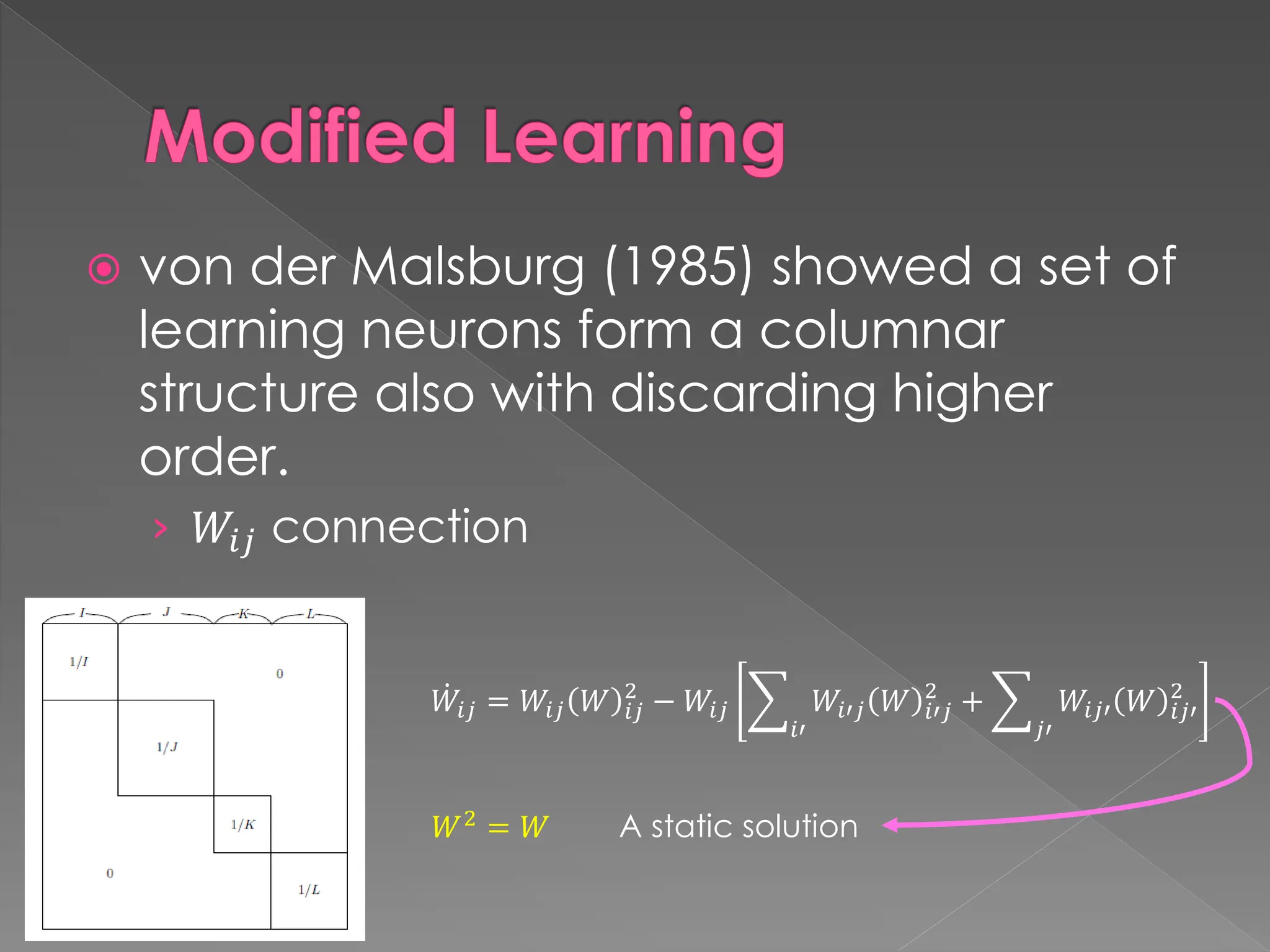
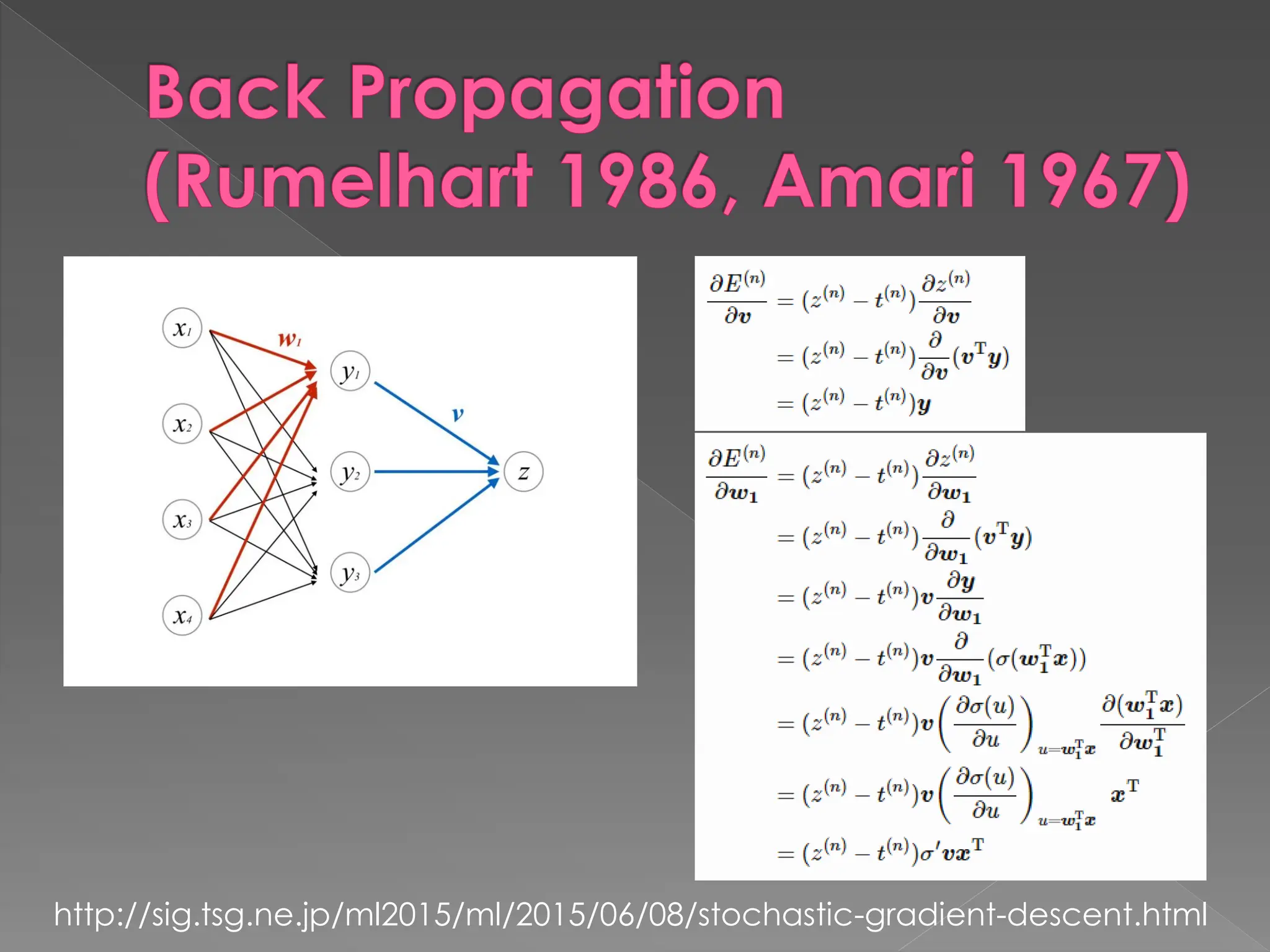
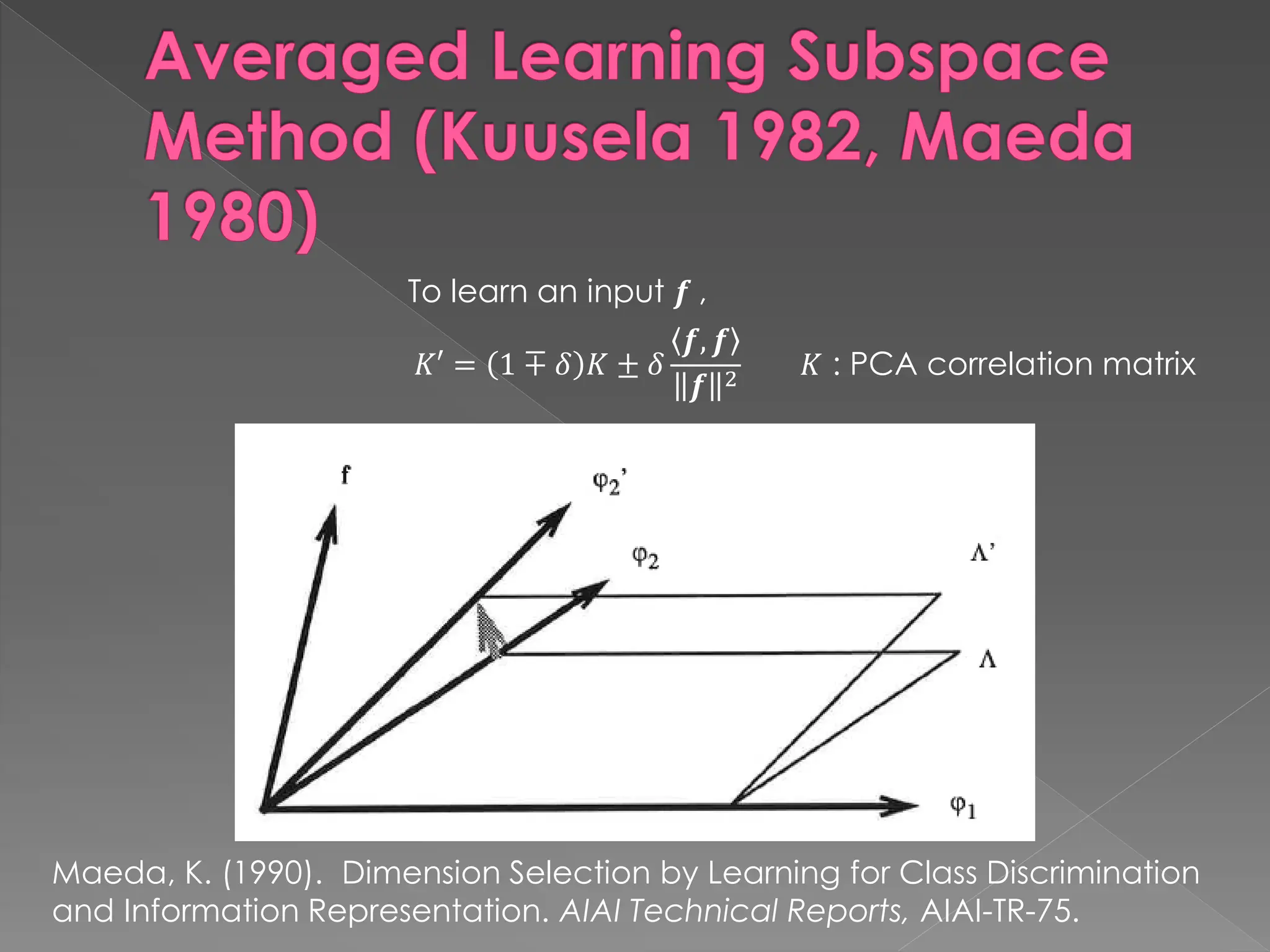
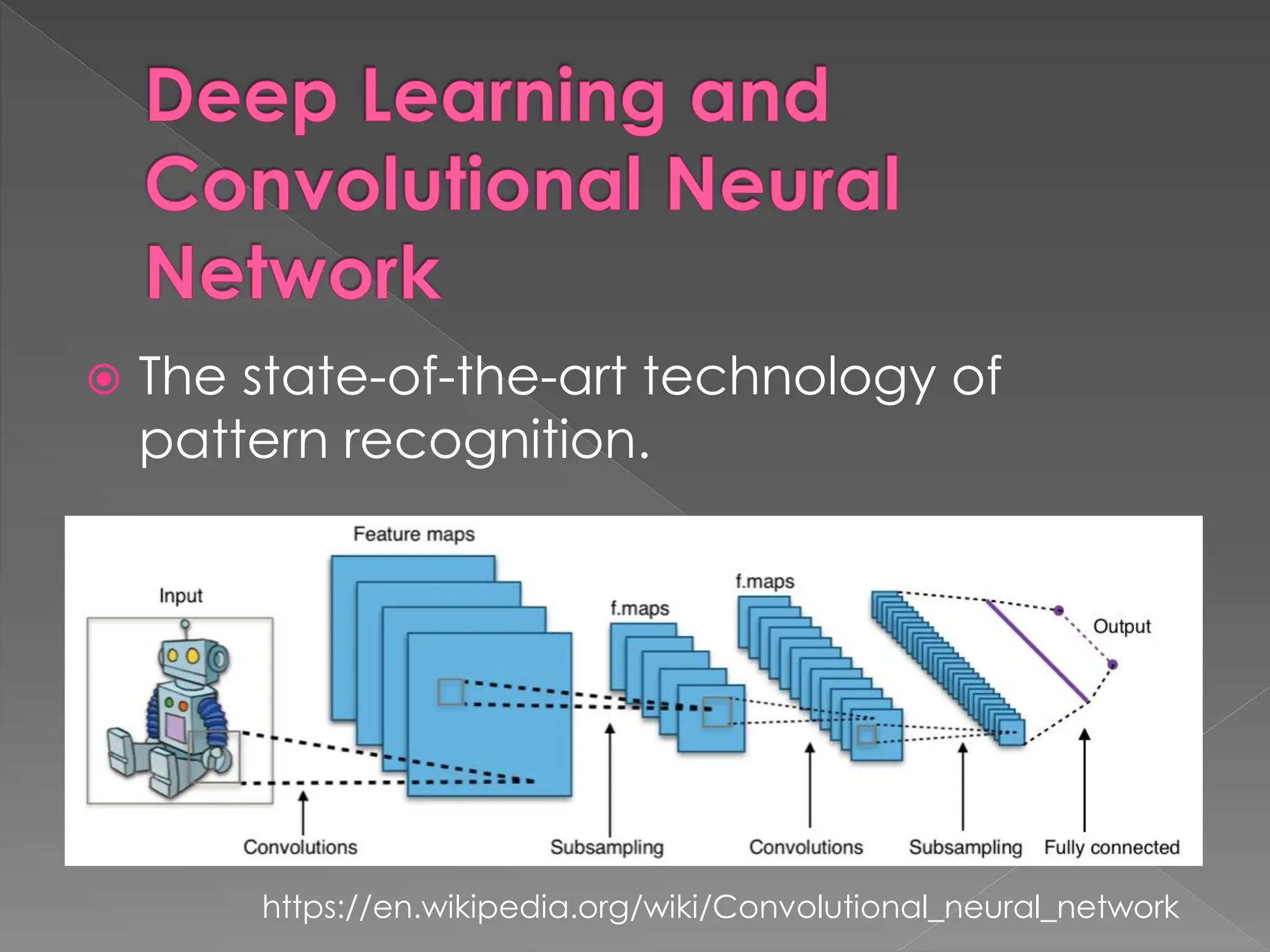
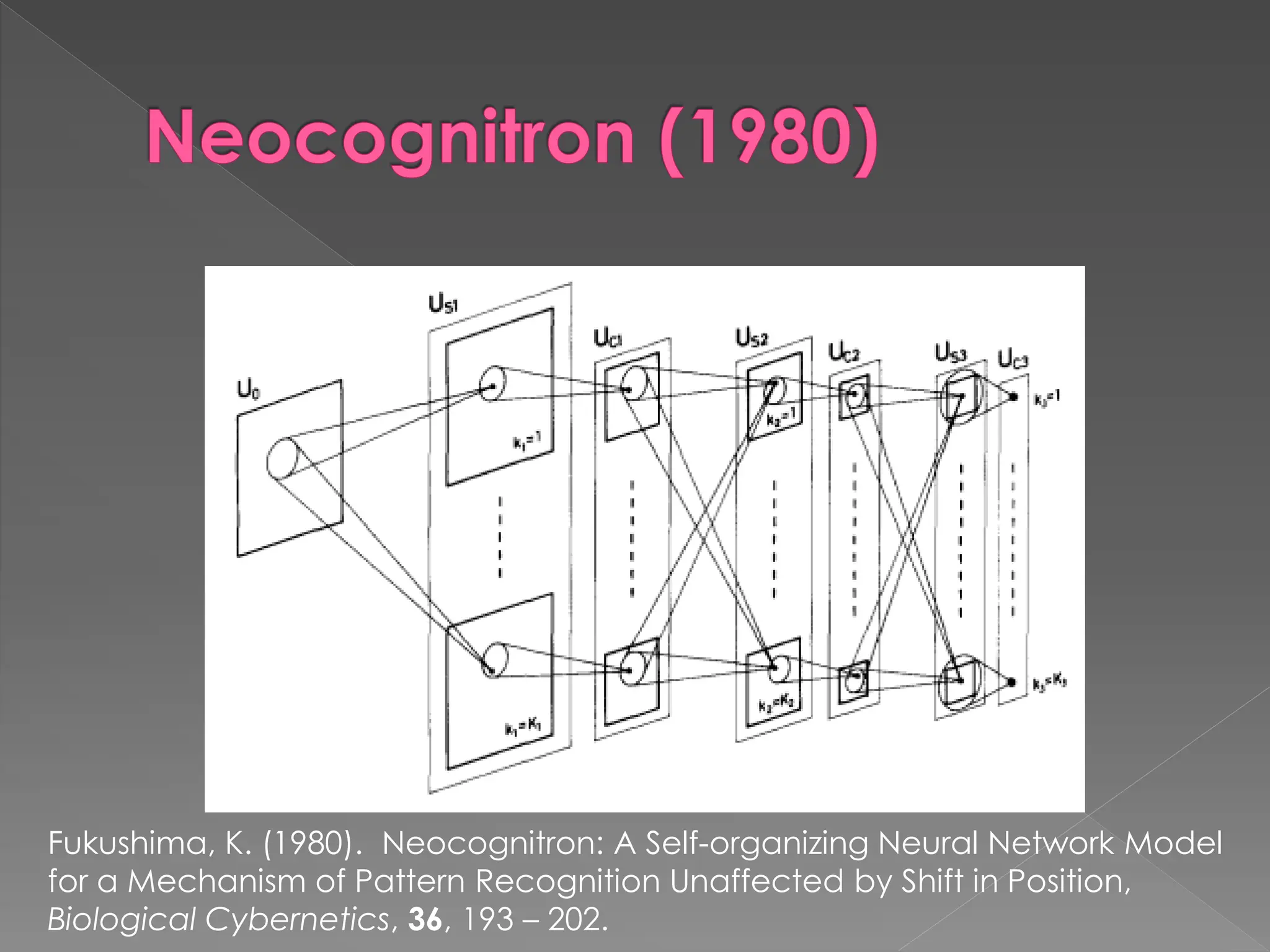
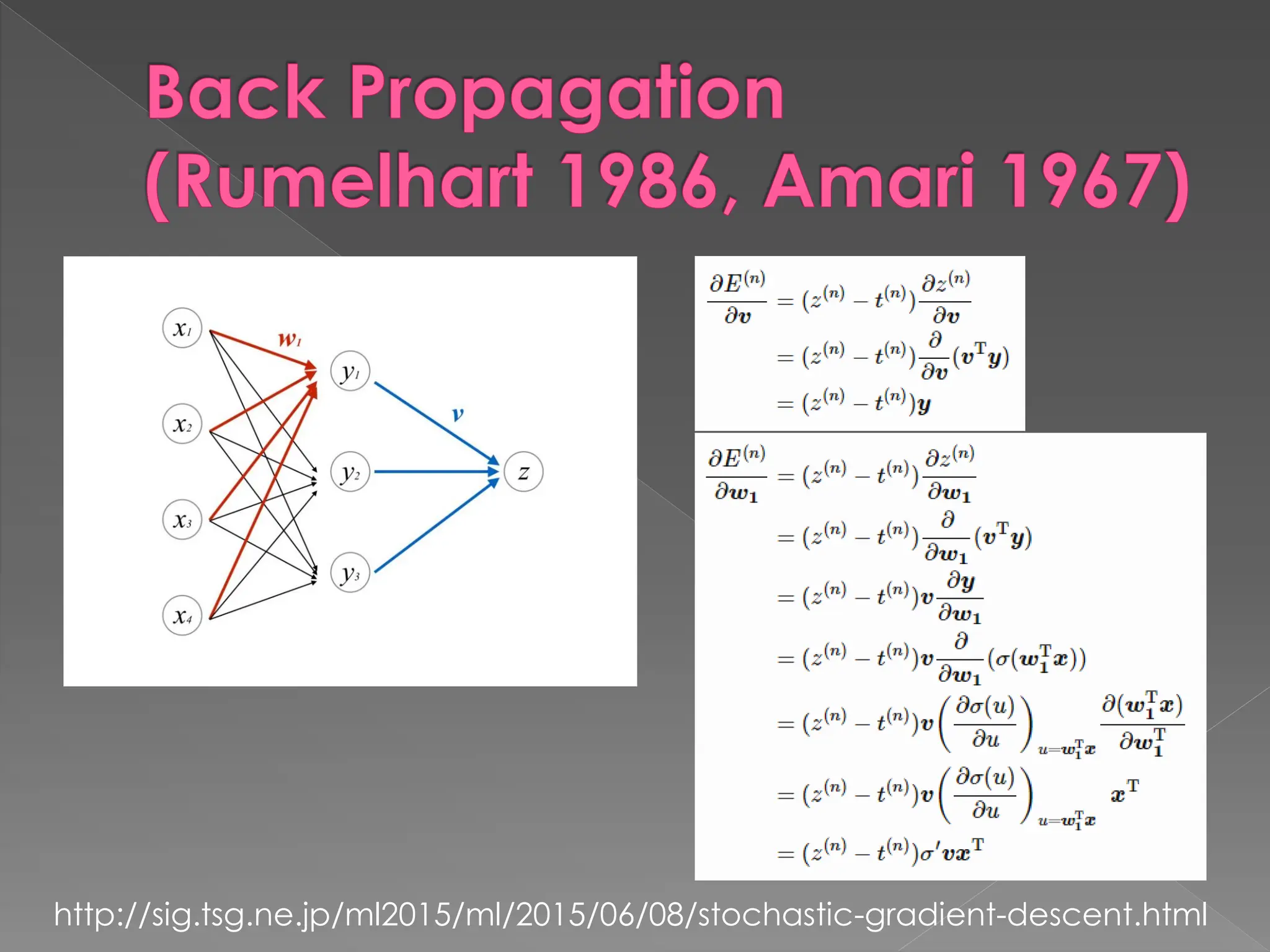
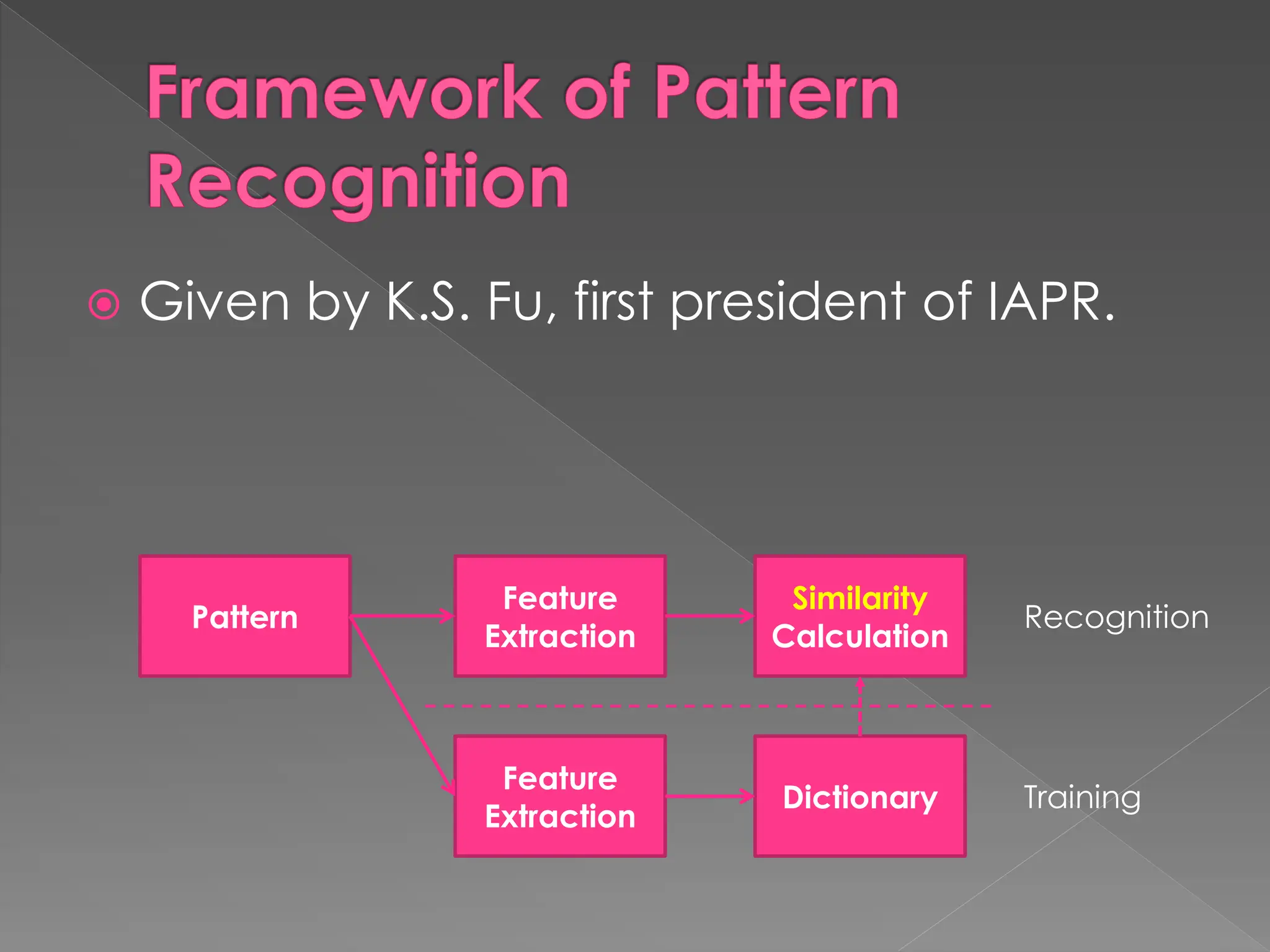
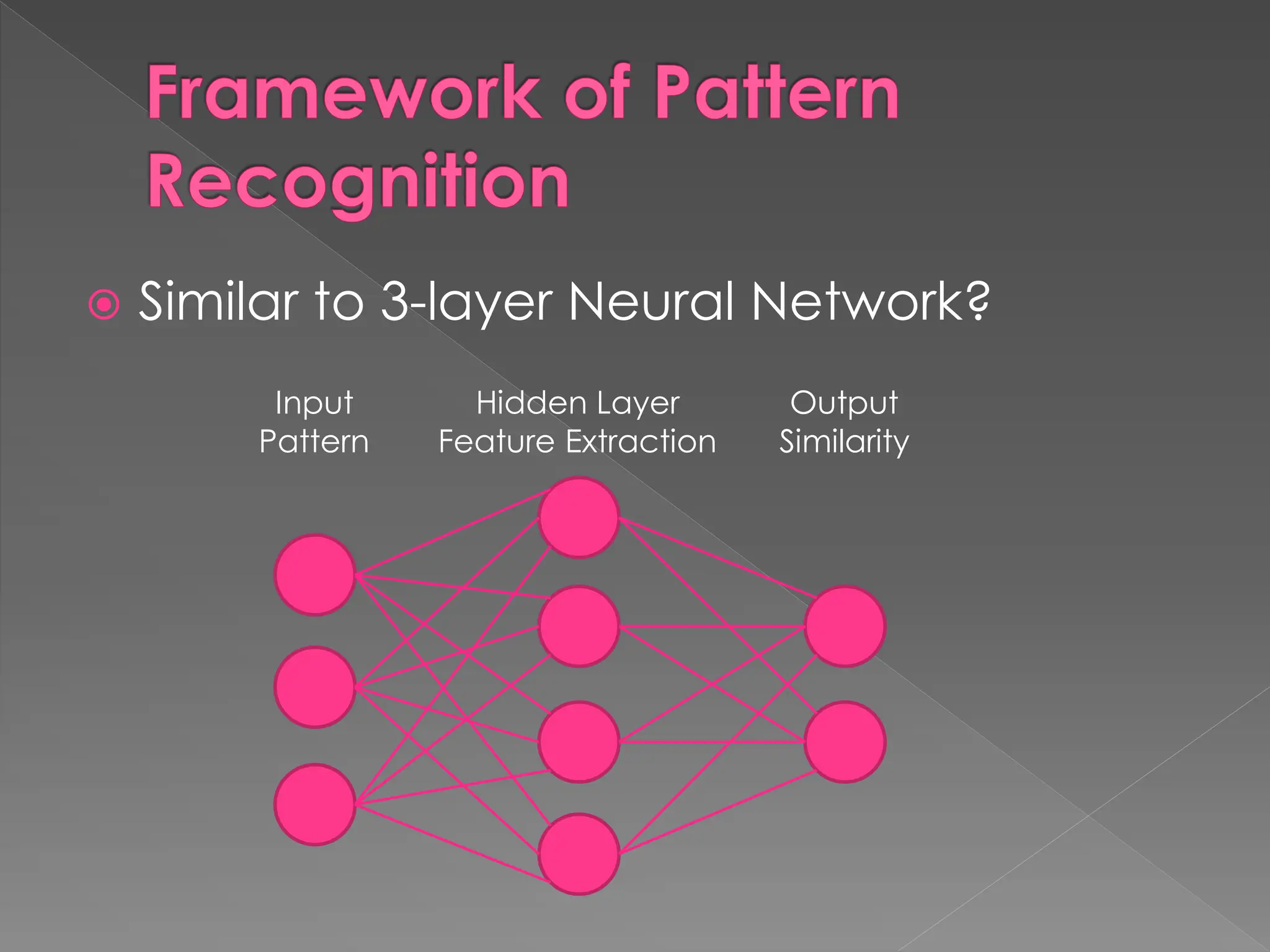
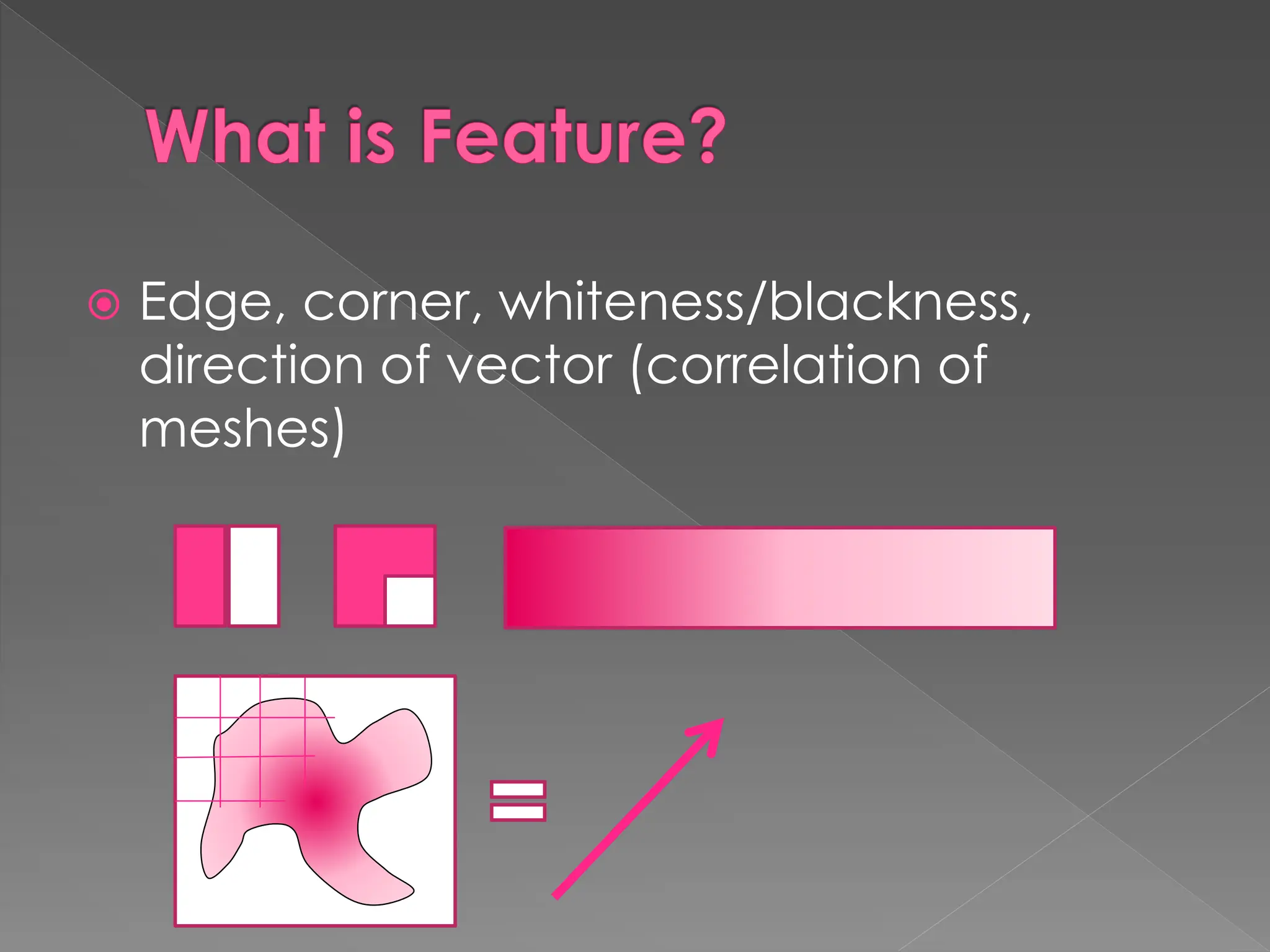
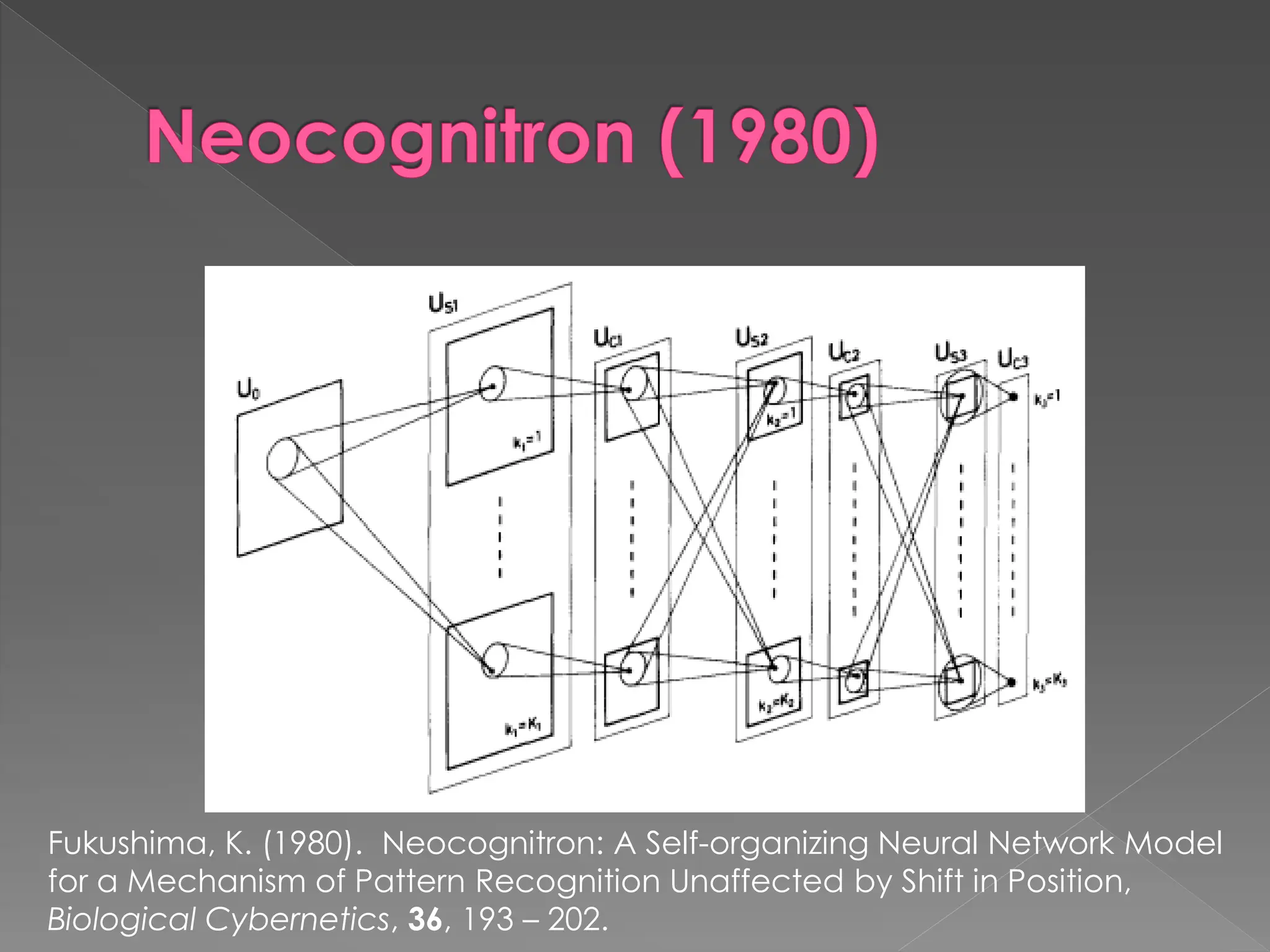
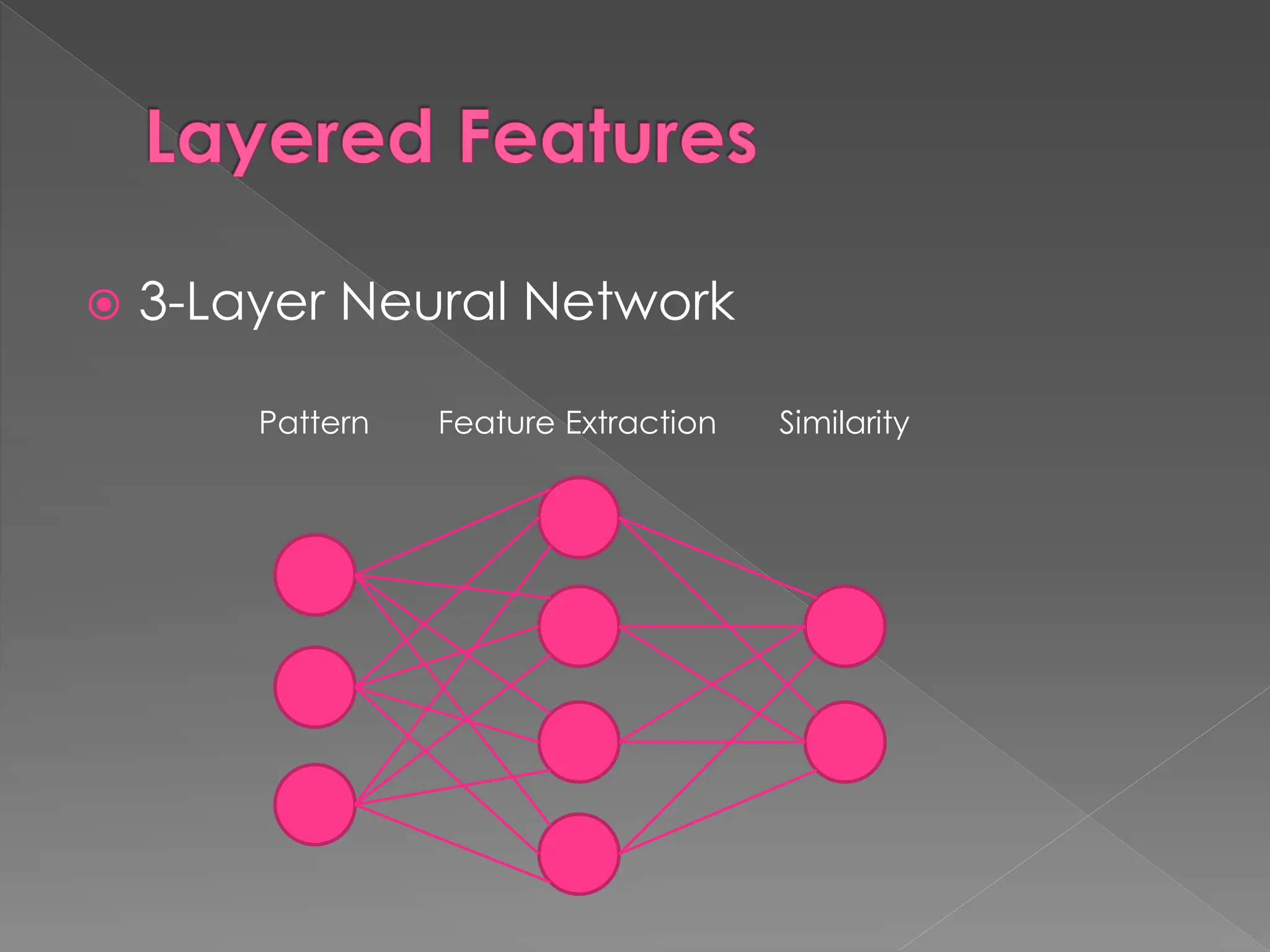
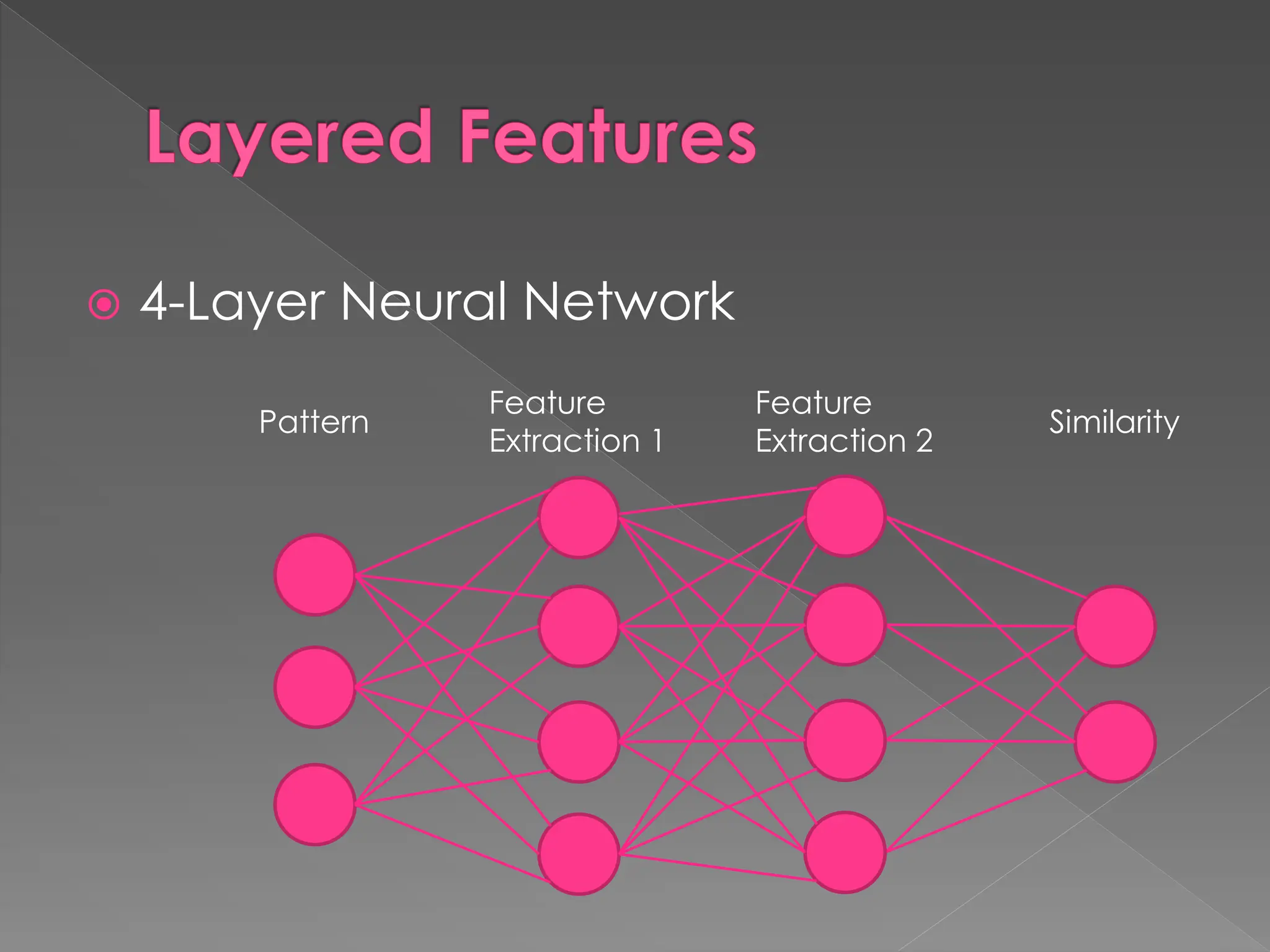
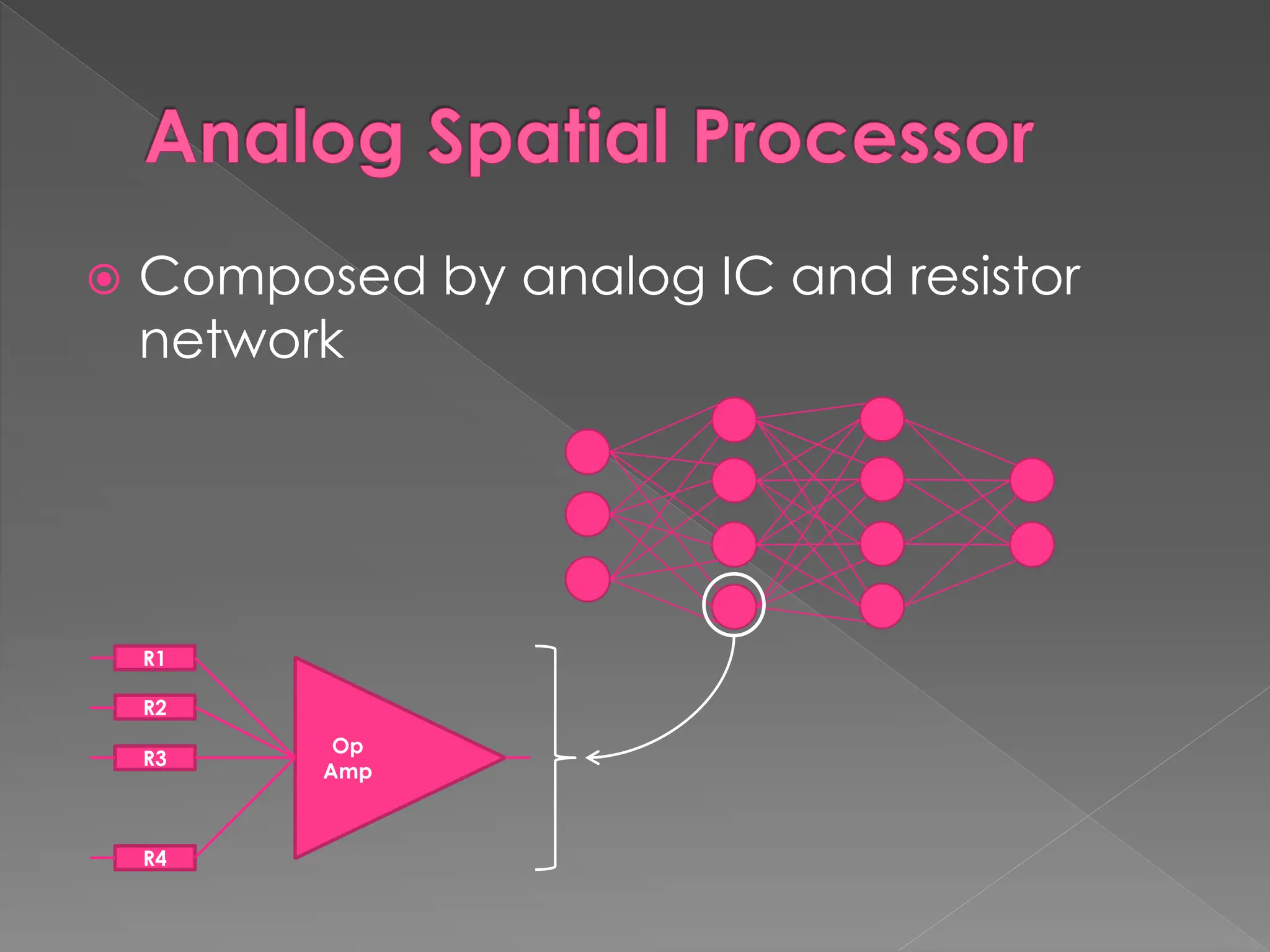
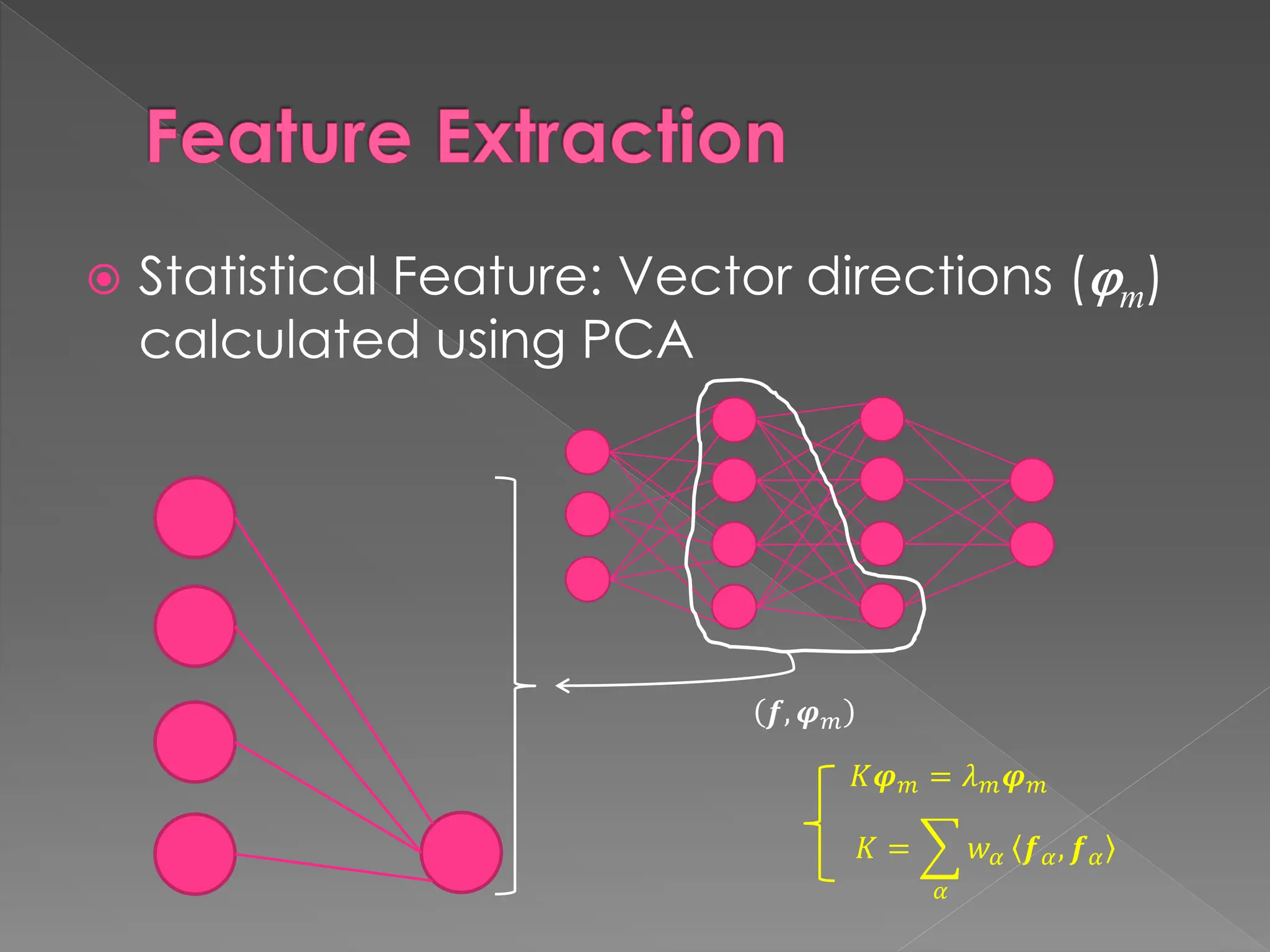
The document discusses the evolution and current state of pattern recognition, highlighting the significance of deep learning and convolutional neural networks as state-of-the-art technologies. It traces the historical development of various pattern recognition models, including the neocognitron and the back propagation algorithm, while emphasizing the importance of returning to fundamental principles in the field. Ultimately, it asserts that while deep learning is powerful, it is not the sole solution and encourages a broader perspective on learning and feature recognition.

1. Pattern Recognition Revisited
Another Story of Pattern Recognition
Is Deep Learning the only way?
Ken-ichi Maeda
ICVSS: Sicily, 22 July 2016

2. Deep Learning and
Convolutional Neural
Network
 The state-of-the-art technology of
pattern recognition.
https://en.wikipedia.org/wiki/Convolutional_neural_network

3. Neocognitron (1980)
Fukushima, K. (1980). Neocognitron: A Self-organizing Neural Network Model
for a Mechanism of Pattern Recognition Unaffected by Shift in Position,
Biological Cybernetics, 36, 193 – 202.

4. Back Propagation
(Rumelhart 1986, Amari 1967)
http://sig.tsg.ne.jp/ml2015/ml/2015/06/08/stochastic-gradient-descent.html

5. Framework of Pattern
Recognition
 Given by K.S. Fu, first president of IAPR.
Feature
Extraction
Similarity
Calculation
Pattern Recognition
Dictionary
Feature
Extraction
Training

6. Framework of Pattern
Recognition
 Similar to 3-layer Neural Network?
Input Hidden Layer Output
Pattern Feature Extraction Similarity

7. What is Feature?
 Edge, corner, whiteness/blackness,
direction of vector (correlation of
meshes)

8. Neocognitron (1980)
Fukushima, K. (1980). Neocognitron: A Self-organizing Neural Network Model
for a Mechanism of Pattern Recognition Unaffected by Shift in Position,
Biological Cybernetics, 36, 193 – 202.

9. Layered Features
 3-Layer Neural Network
Pattern Feature Extraction Similarity

10. Layered Features
 4-Layer Neural Network
Pattern
Feature
Extraction 1
Similarity
Feature
Extraction 2

11. ASPET 70/71 (1970, 1971)
 Analog Spatial Processor Developed by
Electro-Technical Laboratory and
Toshiba
 OCR prototype
http://museum.ipsj.or.jp/en/heritage/ASPET/71.html

12. Analog Spatial Processor
 Composed by analog IC and resistor
network
Op
Amp
R2
R3
R1
R4

13. Feature Extraction
 Geometric Feature: Whiteness/blackness
convolution with Gaussian Function (Pool)
𝑓(𝒓𝑖, 𝜎) = න 𝐺 𝒓𝑖 − 𝒓, 𝜎 𝑓(𝒓)d𝒓
𝐺 𝒓, 𝜎 =
1
2π𝜎2 exp −
𝒓 2
2𝜎2

14. Feature Extraction
 Statistical Feature: Vector directions (m)
calculated using PCA
𝒇, 𝝋𝑚
𝐾𝝋𝑚 = 𝜆𝑚𝝋𝑚
𝐾 = ෍
𝛼
𝑤𝛼 𝒇𝛼, 𝒇𝛼

15. Similarity
 Multiple Similarity Measure: Angle
between Vector and Subspace
𝑆 𝒇 = cos 2 𝜃
= ෍
𝑚=1
𝑀
𝒇, 𝝋𝑚
2
𝒇 2

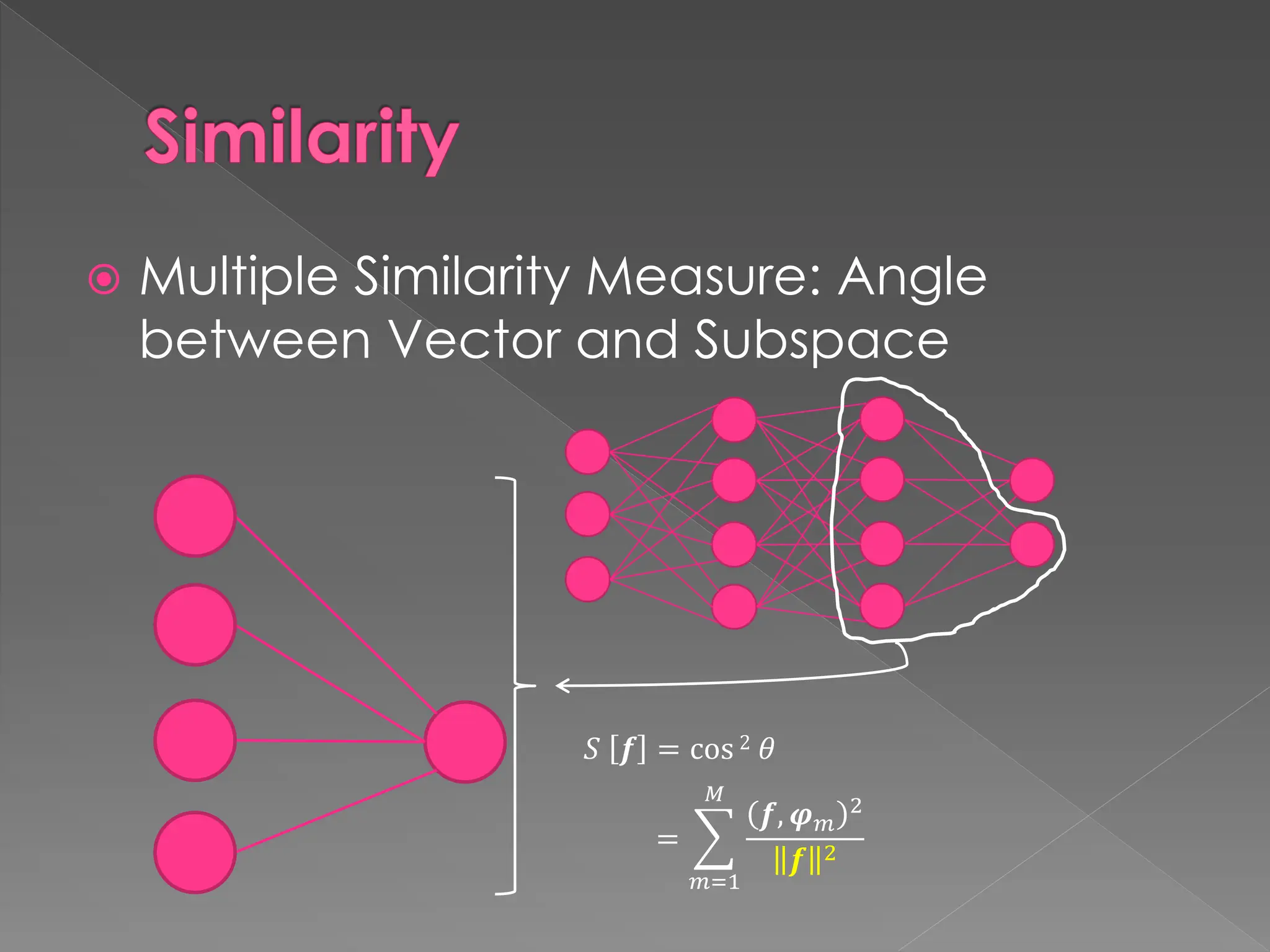
16. Similarity Visualisation
 Angle between a vector and a subspace
(f*: Nearest vector of f in the subspace)
S [f] = cos2 
𝝋1
𝝋2
f

f*

17. Problems in Features
 Is convolution with Gaussian Function
effective enough to recognize Kanji
(Chinese characters)?

18. Extended Features
 We need more complex features, e.g.,
edges
› Gaussian-weighted Hermite Polynomials
𝒓 = 𝑥𝒊 + 𝑦𝒋
𝜕𝑚+𝑛
𝜕𝑥𝑚𝜕𝑦𝑛 𝑓 𝒓, 𝜎 = න
𝜕𝑚+𝑛
𝜕𝑥𝑚𝜕𝑦𝑛 𝐺 𝒓 − 𝒓′
, 𝜎 𝑓(𝒓′)d𝒓′
=
𝑚!𝑛!
− 2
𝑚+𝑛 𝑓𝑚𝑛 𝒓, 𝜎
𝑓𝑚𝑛 𝒓, 𝜎 = න
1
𝑚! 𝑛!
𝜎
2
𝑚+𝑛 𝐺 𝒓 − 𝒓′, 𝜎 𝐻𝑚
𝑥 − 𝑥′
𝜎
𝐻𝑛(
𝑦 − 𝑦′
𝜎
)𝑓(𝒓′)d𝒓′

19. Basic Equation of Figure and
Scale Space
 Proposed by Iijima (1959) before scale
space by Witkin (1983).
𝑓(𝒓𝑖, 𝜎) = න 𝐺 𝒓𝑖 − 𝒓, 𝜎 𝑓(𝒓)d𝒓
𝛁2 −
𝜕
𝜕𝜏
𝑓 𝒓, 𝜎 = 0
𝜏 =
𝜎2
2

20. Gaussian-weighted Hermite
Polynomials (Maeda 1982)
 Like Gabor Functions

21. Similar Feature (Gabor)
 Equal interval 0 crossing

22. Similar Feature (Rubner 1990)
 Made using Oja’s equation.
 Look like Gaussian-weighted Hermite
Polynomials

23. Similar Feature (Linsker 1988)
 Layered Linsker Network

24. Similar Feature (MacKay
1990)
 Polar Representation

25. Deep Learning Features
 Result of deep learning

26. Hebbian Learning
 A basic concept of correlation learning
presented by Hebb (1949)
› 𝑥𝑖 input, 𝑦 output, 𝑤𝑖 connection,
𝜂 learning weight
∆𝑤𝑖 = 𝜂𝑥𝑖𝑦
𝑦 = ෍
𝑗
𝑤𝑗 𝑥𝑗

27. Modified Learning
 Oja (1982) showed that a neuron model
could generate a subspace {𝝋m}.
› 𝜉𝑖 input, 𝜇𝑖 connection, 𝜂 output
› Modified learning equation assuming 𝛾
(positive learning parameter) is small.
𝜇𝑖 𝑡 + 1 = 𝜇𝑖 𝑡 + 𝛾𝜂 𝑡 𝜉𝑖 𝑡 − 𝜂 𝑡 𝜇𝑖 𝑡 + 𝑂 𝛾2
𝝋𝑚 = T(𝜇1, 𝜇2, ⋯ , 𝜇𝑖, ⋯ , 𝜇𝐼)
𝜇𝑖 𝑡 + 1 =
𝜇𝑖 𝑡 + 𝛾𝜂 𝑡 𝜉𝑖 𝑡
σ𝑗=1
𝐼
𝜇𝑖 𝑡 + 𝛾𝜂 𝑡 𝜉𝑖 𝑡 2 1/2 (original modification)

28. Modified Learning
 von der Malsburg (1985) showed a set of
learning neurons form a columnar
structure also with discarding higher
order.
› 𝑊𝑖𝑗 connection
ሶ
𝑊𝑖𝑗 = 𝑊𝑖𝑗 𝑊 𝑖𝑗
2
− 𝑊𝑖𝑗 ෍
𝑖′
𝑊𝑖′𝑗 𝑊 𝑖′𝑗
2
+ ෍
𝑗′
𝑊𝑖𝑗′ 𝑊 𝑖𝑗′
2
𝑊2
= 𝑊 A static solution

29. What is Learning?
 Learning is used to find geometric
features.
 Learning is the training phase for
recognition.
› To find correlation features.

30. Back Propagation
(Rumelhart 1986, Amari 1967)
http://sig.tsg.ne.jp/ml2015/ml/2015/06/08/stochastic-gradient-descent.html

31. Learning Subspace Method
(1979)
Maeda, K. (1990). Dimension Selection by Learning for Class Discrimination
and Information Representation. AIAI Technical Reports, AIAI-TR-75.
𝐴′
= 𝐸 ± 𝛿
𝒇, 𝒇
𝒇 2 𝐴
A : projection
E : unit matrix
To learn an input 𝒇 ,

32. Averaged Learning Subspace
Method (Kuusela 1982, Maeda
1980)
Maeda, K. (1990). Dimension Selection by Learning for Class Discrimination
and Information Representation. AIAI Technical Reports, AIAI-TR-75.
To learn an input 𝒇 ,
𝐾′ = 1 ∓ 𝛿 𝐾 ± 𝛿
𝒇, 𝒇
𝒇 2 𝐾 : PCA correlation matrix

33. Conclusion
 Deep Learning is the state-of-the-art
technique in pattern recognition and
machine learning, but similar concepts
and results existed before.
 It is quite a powerful method, but is not
the only solution.
 We sometimes should return to the
principle, so that we can continue
making progress.

34. Guidance on the future
 Learn from the past, but never stick to it
only.
 Back to the principle, back to what you
see.
 Everything is useful if you can correctly
see.
The future is yours!

35. References of Historical Works
 Amari, S. (1967). Theory of Adaptive Pattern Classifiers, IEEE Transactions EC-1, 299–307.
 Fukushima, K. (1980). Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition
Unaffected by Shift in Position, Biological Cybernetics, 36, 193 – 202.
 Hebb, D. O. (1949). The Organization of Behavior, Wiley.
 Hubel, D. H. and Wiesel, T. N. (1962). Receptive Fields, Binocular Interaction, and Fundamental Architecture in the Cat's Visual
Cortex, J. Physiol., 160, 106-154.
 Iijima, T. (1959). Basic Theory of Pattern Observation, Technical Group on Automata and Automatic Control, IECE, 1-37. In
Japanese.
 Iijima, T. (1963). Basic Theory of Feature Extraction from Visual Patterns, J. IECE, 46 (11), 1714. In Japanese.
 Iijima, T., et al. (1972). A Theoretical Study of Pattern Identification by Matching Method in Proc. of First USA-Japan Computer
Conf., 42–48.
 Iijima, T., et al. (1973). A Theory of Character Recognition by Pattern Matching Method, Proc. of First Int. Joint Conf. on Pattern
Recognition, 50-56.
 Irie, B. and Miyake, S. (1988). Capabilities of Three-Layered Perceptrons, Proc. of ICNN, Vol. 1, 641 – 648.
 Kohohen, T. et al. (1979). Spectral Classification of Phoneme by Learning Subspace, Proc. of Int. Conf. on Acoustics, Speech,
and Signal Processing, 807 – 809.
 Kuusela, M and Oja, E. (1982). Averaged Learning Subspace Method for Spectral Pattern Recognition, Proc. Of the 6th Int.
Cong. on Pattern Recognition (ICPR ‘82), 134 – 137.
 Linsker, R. (1988). Self-Organization in a Perceptual Network, Computer, 21 (3), 105-117.
 MacKay, D. J. C., et al. (1990). Analysis of Linsker's Simulations of Hebbian Rules, Neural Computation, 2 (2), 173-187.
 Maeda, K. (1980). Pattern Recognition Apparatus, Japanese Patent Public Disclosure, 137483/81, 1980
 Maeda, K., et al. (1982). Hand-printed Kanji Recognition by Pattern Matching Method, Proc. of the 6th Int. Conf. on Pattern
Recognition (ICPR '82), 789–792.
 Maeda, K. (1990). Dimension Selection by Learning for Class Discrimination and Information Representation. AIAI Technical
Reports, AIAI-TR-75.
 von der Malsburg, C. (1985). Nervous Structures with Dynamical Links, Ber. Bunsenges. Phys. Chem., 89, 703-710.
 Oja, E. (1982). A Simplified Neuron Model as a Principal Component Analyzer, J. Math. Biology, 15 (3), 267-273.
 Rubner, J., et al. (1990). A Self-Organizing Network for Complete Feature Extraction, Proc. of Int. Conf. on Parallel Processing in
Neural Systems and Computers, 365-368.
 Rumelhart, David E.; Hinton, Geoffrey E., Williams, Ronald J. (1986). Learning representations by back-propagating errors,
Nature 323 (6088): 533–536.
 Widrow, B., et al. (1960). Adaptive Switching Circuits, IRE WESCON Convention Record 4: 96-104.
 Witkin, A. P. (1983). Scale-space filtering, Proc. 8th Int. Joint Conf. Art. Intell.,1019–1022.