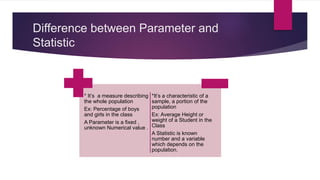
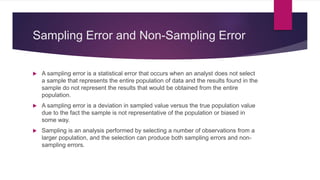
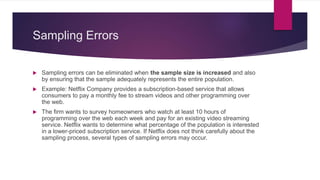
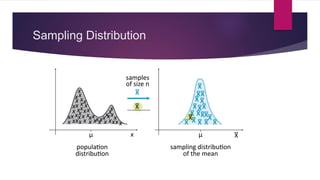
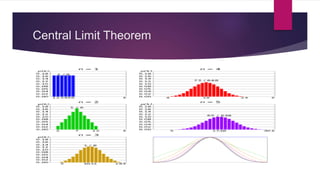
This document discusses key concepts in sampling and statistical inference: - Parameters describe characteristics of entire populations, while statistics describe characteristics of samples. - Sampling distributions describe the distribution of sample statistics if multiple samples are drawn. - As sample size increases, sampling distributions approach a normal distribution due to the central limit theorem. - Statistical inference allows using sample data to make inferences about unknown population parameters.

1. Sampling and
Statistical Inference
DR.B.MAHAMMAD RAFEE
ASSOCIATE PROFESSOR, DEPARTMENT OF COMMERCE AND MANAGEMENT STUDIES, BRINDAVAN
COLLEGE, BANGALORE

2. Parameter and Statistic
 Parameter is a measure of characteristic of an
entire population( a mass of all units under
consideration that shares common
characteristics) based on all the elements
within the population.
 For Ex: Percentage of Young Population in the
Country, Percentage of Boys out 100 students
in the class etc.,

3. Statistic
 Statistic is a measure of Characteristic saying something about a fraction(a
sample) of the population under the study or can say a exact number. A sample in
Statistics is a part or portion of a population.
 Example: In a class of 100 students how many students using I-phone’s for
example say 60.
 It is a known number and a variable which depends on the portion of the
population.
 Statistic acquired from different samples will vary, depending on the samples.

4. Difference between Parameter and
Statistic
* It’s a measure describing
the whole population
Ex: Percentage of boys
and girls in the class
A Parameter is a fixed ,
unknown Numerical value .
*It’s a characteristic of a
sample, a portion of the
population
Ex: Average Height or
weight of a Student in the
Class
A Statistic is known
number and a variable
which depends on the
population.

5. MCQ on Parameter and Statistic
 A parameter is:
 a. a sample characteristic
 b. a population characteristic
 c. unknown
 d. normal normally distributed
 A statistic is:
 a. a sample characteristic
 b. a population characteristic
 c. unknown
 d. normally distributed

6.  Which of the following statements best describes the relationship between a parameter and a statistic?
A. A parameter has a sampling distribution with the statistic as its mean.
B. A parameter has a sampling distribution that can be used to determine what values the statistic is likely to have in repeated samples.
C. A parameter is used to estimate a statistic.
 D. A statistic is used to estimate a parameter.
 A sampling distribution is the probability distribution for which one of the following:
A. A sample
 B. A sample statistic
C. A population
 D. A population parameter Any measure of the population is called:
Finite
 Parameter
Without replacement
Random

7. Sample Statistic and Population
Parameters: Statistical notations
 In population parameter, population proportion is represented by P, mean is
represented by µ (Greek letter mu), σ2 represents variance, N represents
population size, σ (Greek letter sigma) represents standard deviation, σx̄
represents Standard error of the mean, σ/µ represents Coefficient of variation, (X-
µ)/σ represents standardized variate (z), and σp represents standard error of
proportion.
 In sample statistics, mean is represented by x
̄ (x-bar), sample proportion is
represented by p
̂ (p-hat), s represents standard deviation, s2 represents variance,
the sample size is represented by n, sx̄ represents Standard error of the mean, sp
represents standard error of a proportion, s/(x
̄ ) represents Coefficient of variation,
and (x-x
̄ )/s represents standardized variate (z).

8. Sampling Error and Non-Sampling Error
 A sampling error is a statistical error that occurs when an analyst does not select
a sample that represents the entire population of data and the results found in the
sample do not represent the results that would be obtained from the entire
population.
 A sampling error is a deviation in sampled value versus the true population value
due to the fact the sample is not representative of the population or biased in
some way.
 Sampling is an analysis performed by selecting a number of observations from a
larger population, and the selection can produce both sampling errors and non-
sampling errors.

9. Sampling Errors
 Sampling errors can be eliminated when the sample size is increased and also
by ensuring that the sample adequately represents the entire population.
 Example: Netflix Company provides a subscription-based service that allows
consumers to pay a monthly fee to stream videos and other programming over
the web.
 The firm wants to survey homeowners who watch at least 10 hours of
programming over the web each week and pay for an existing video streaming
service. Netflix wants to determine what percentage of the population is interested
in a lower-priced subscription service. If Netflix does not think carefully about the
sampling process, several types of sampling errors may occur.

10. Sampling Error
 Examples of Sampling Errors
 A population specification error means that Netflix does not understand the specific types of
consumers who should be included in the sample. If, for example, Netflix creates a population of
people between the ages of 15 and 25 years old, many of those consumers do not make the
purchasing decision about a video streaming service because they do not work full-time. On the
other hand, if Netflix put together a sample of working adults who make purchase decisions, the
consumers in this group may not watch 10 hours of video programming each week.
 Selection error also causes misrepresentations in the results of a sample, and a common example
is a survey that only relies on a small portion of people who immediately respond. If Netflix makes
an effort to follow up with consumers who don’t initially respond, the results of the survey may
change. Furthermore, if Netflix excludes consumers who don’t respond right away, the sample
results may not reflect the preferences of the entire population.

11. MCQ on Sampling Error
 _____ occurs when the sample used in the study is not representative of the whole
population.
 Margin of error
 Sampling error
 Non-sampling error
 Population specification
 Which of these is a technique to minimize sampling error?
 Increase the sample size
 Divide the population into groups
 Know your population
 Train your team

12. Non-Sampling Error
 A non-sampling error is a statistical term that refers to an error that results during
data collection, causing the data to differ from the true values.
 A non-sampling error refers to either random or systematic errors, and these
errors can be challenging to spot in a survey, sample, or census.
 The higher the number of errors, the less reliable the information is.
 For example, non-sampling errors can include but are not limited to, data entry
errors, biased survey questions, biased processing/decision making, non-
responses, inappropriate analysis conclusions, and false information provided by
respondents.

13. Special consideration in Sampling and
Non-Sampling Errors
 Special Considerations
 While increasing sample size can help minimize sampling errors, it will not have any effect on
reducing non-sampling errors. This is because non-sampling errors are often difficult to detect,
and it is virtually impossible to eliminate them.
 Non-sampling errors include non-response errors, coverage errors, interview errors, and
processing errors. A coverage error would occur, for example, if a person were counted twice in a
survey, or their answers were duplicated on the survey. If an interviewer is biased in their
sampling, the non-sampling error would be considered an interviewer error.
 In addition, it is difficult to prove that respondents in a survey are providing false information—
either by mistake or on purpose. Either way, misinformation provided by respondents count as
non-sampling errors and they are described as response errors.
 Technical errors exist in a different category. If there are any data-related entries—such as coding,
collection, entry, or editing—they are considered processing errors.

15. Sampling Distribution
 A sampling distribution is a probability distribution of a statistic obtained from a
larger number of samples drawn from a specific population. The sampling
distribution of a given population is the distribution of frequencies of a range of
different outcomes that could possibly occur for a statistic of a population.
 In statistics, a population is the entire pool from which a statistical sample is
drawn. A population may refer to an entire group of people, objects, events,
measurements etc.,

16. Sampling Distribution
 For Example: A Medical researcher want to calculate average weight of all babies
born in India, he will take the repeated samples from different states of India .
Where each sample is having its own mean and the distribution of sample mean
is known as the sample distribution.
 The average weight computed for each sample set is the sampling distribution of
the mean. Other statistics, such as standard deviation and variance and range
can be calculated from sample data. The standard deviation and variance
measure the variability of sampling distribution.

17. Sampling Distribution

18. Degrees of Freedom
 Degrees of Freedom refers to the maximum number of logically independent
values, which are values that have the freedom to vary, in the data sample.
 The statistical formula to determine degrees of freedom is quite simple. It states
that degrees of freedom equal the number of values in a data set minus 1, and
looks like this:
 df = N-1
 Where N is the number of values in the data set (sample size). Take a look at the
sample computation.
 If there is a data set of 4, (N=4).

19. Degree of Freedom
 Call the data set X and create a list with the values for each data.
 For this example data, set X includes: 15, 30, 25, 10
 This data set has a mean, or average of 20. Calculate the mean by adding the values and dividing
by N:
 (15+30+25+10)/4= 20
 Using the formula, the degrees of freedom would be calculated as df = N-1:
 In this example, it looks like, df = 4-1 = 3
 This indicates that, in this data set, three numbers have the freedom to vary as long as the mean
remains 20.
 Degrees of Freedom are commonly discussed in relation to various forms of hypothesis testing in
statistics, such as a Chi-Square. It is essential to calculate degrees of freedom when trying to
understand the importance of a Chi-Square statistic and the validity of the null hypothesis.

20. Standard error
 “standard error” of a statistic refers to the estimate of the standard deviation of the
sample mean from the true population mean. On other hand, standard deviation
measures the dispersion of each individual value from the sample mean, the standard
error of mean measures the dispersion of all the sample means around the population
mean.
 The formula for standard error can be derived by dividing the sample standard
deviation by the square root of the sample size. Standard Error = s / √n
 Where,
 s: √Σn
i(xi-x
̄ )2 / n-1
 xi: ith Random Variable
 x
̄ : Sample Mean
 n: Sample Size

21. Central Limit Theorem
 Central limit theorem states ,the sampling distribution of the sample means
approaches a normal distribution as the sample size gets larger.
 All this is saying is that as you take more samples, especially large ones, your
graph of the sample means will look more like a normal distribution.

22. Central Limit Theorem

23. Statistical inference
 Statistical inference is the process of using data analysis to deduce properties of
an underlying distribution of probability. Inferential statistical analysis infers
properties of a population, for example by testing hypotheses and deriving
estimates. It is assumed that the observed data set is sampled from a larger
population.
 Statistical inference consists in the use of statistics to draw conclusions about
some unknown aspect of a population based on a random sample from that
population.
 Example : Testing the short term and long term relationship among the variables.