Statistical inference uses probability concepts to make conclusions about populations based on samples. It refers to using sample data to draw inferences about characteristics of the overall population. 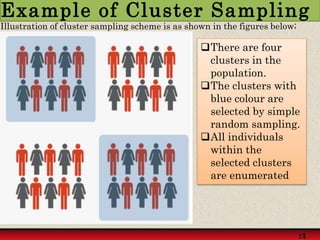Key terms include: - Population is the entire group being studied - Sample is a subset of the population - Parameter describes a characteristic of the population (unknown) - Statistic describes a characteristic of the sample (known) Probability sampling methods, like simple random sampling, give every member of the population a known chance of being selected in the sample. This allows estimating sampling error and making statistical inferences about the population. Non-probability sampling does not give all members an equal chance of selection.

1. INTRODUCTION
TO STATISTICAL
INFERENCE
1
1

2. 1.1
BASIS OF
STATISTICAL
INFERENCE
2

3. BASIS OF STATISTICAL INFERENCE
3
Statistical inference is the branch of statistics which is concerned with
using probability concept to deal with uncertainty in decision making. It
refers to the process of selecting and using sample to draw inference about
population from which sample is drawn. It can defined as the branch of
statistics that uses random sample of data taken from a population to
describe and make categorical statement about the population from where
the sample was drawn. The single goal of statistical inference is to
determine the characteristics of the population from the sample.
Inferential statistics are valuable when examination of each member of an
entire population is not convenient or possible.
For example, to measure the diameter of each nail that is manufactured in a
mill is impractical. You can measure the diameters of a representative
random sample of nails. You can use the information from the sample to
make generalizations about the diameters of all of the nails.
As we begin to use sample data to draw conclusions about a wider
population, we must be clear about some terminologies.

4. Terminologies
: A population is a collection of all possible individuals, objects or
measurements of interest in a statistical investigation. For example; all male
students in University of Medical Sciences, Ondo
: A sample is a small proportion or fractional part of the population
interest. It is a subset of the population. For example; male students in
Faculty of Science, University of Medical Sciences, Ondo
: This is a number that describes some characteristics of the
population. They are usually denoted with Greek letters. In statistical
practice, the value of a parameter is not known because we cannot examine
the entire population. Population mean (𝜇) is a parameter.
: This is a number that describes some characteristics of a sample.
The value of a statistic can be computed from the sample data. We often use a
statistic to estimate an unknown parameter. The sample mean (𝑥) is a
statistic. They are denoted with Latin letters
In summary, statistics comes from the samples and parameters come from
population.
4
Sample Population
Mean 𝑥 𝜇 (mu)
Standard deviation S 𝜎 (Sigma)

5. Sampling Theory
Sampling theory is the study of relationships existing between a
population and samples drawn from it. For the sample results to
have a worthwhile meaning, it is necessary that the samples
possesses the following essentials.
: A sample should be selected in such a way
that it truly represents the population otherwise the result
obtained will be misleading. To ensure representativeness, the
random method of selection should be used.
: The size of the sample must be adequate otherwise
it may not represent the characteristics of the population
: All items of the sample should be selected
independently of one another. That is, all items should have
equal chance of being selected in the sample.
: There should be no basic difference in the
nature of units of the population and that of the sample.
5

6. Sampling Unit and Sampling Frame
Sampling unit is the division of the population into a finite
number of distinct and identifiable units. The units must cover
the entire population and they must not overlapped in the sense
that every element in the population belongs to one and only one
unit. For example, in sampling the people in a town, the units
may be an individual person, household or all the person living
in the sampled city or street.
Sampling frame is the list of all items/units in the sampling
units (i.e the population to be covered) from where the sample
will be selected. It can also be regarded as the list of all the
sampling units with proper identification. The frame may
consist of either a list of units or map of area ( in case sample of
area is being taken) such that every element in the population
belongs to one and only one unit. For the sampling frame to be
reliable, it must possess the following features;
6

7. Features of reliable Sample Frame
 The frame must be accurate
 The frame must be free of omission and duplication (no
overlapping)
 The frame must be adequate
 The frame must be up-to-date
 The frame must cover the whole population and should be well
defined
7
Reasons for Sampling
The foremost purpose of sampling is to gather maximum information about
the population under consideration at minimum cost, time and resources.
Precisely, sampling is inevitable in the following situations:
 when population is infinite;
 when the item or unit is destroyed under investigation;
 when the results are required in a short time;
 when resources are limited particularly in respect of money and trained
persons;
 when population is either constantly changing or in a state of movement;
 when the items or units are scattered.

8. SAMPLING AND NON-SAMPLING ERROR
8
The difference between an estimated value and the population true value is called an
error. Since a sample estimate is used to describe a characteristic of a population. A
sample being only a part of population cannot provide a perfect representation of the
population, no matter how carefully the sample is selected. Generally it is seen that
an estimate is rarely equal to the true value and we may think that how close the
sample estimate will be to the population true value. There are two kind of errors:
Sampling Errors (Random Errors) and Non-Sampling Errors (Non-random errors)
Sampling Error: This is the difference between the value of a statistic obtained from
an observed random sample and the value of corresponding population parameter
being estimated. Let 𝑥 be the sample statistic used to estimate the population
parameter 𝜇, then sampling error denoted by E is 𝐸 = 𝑥 − 𝜇. The value of Sampling
Error reveals the precision of the estimate. The smaller the sampling error, the
greater will be the precision of the estimate. The sampling error can be reduced:
 By increasing sample size
 By improving sampling design
 By using supplementary information
Non-Sampling Error: The error that are caused by sampling the wrong population of
interest, response bias as well as those made by an investigator in collecting,
analysing and reporting the data are all classified as non-sampling error or non-
random error. These errors are present in a complete census as well as in sample
survey.

9. Sampling and sampling Methods
9
The process of obtaining samples from the entire population is called
Sampling while the procedure/technique/scheme/manner through which
the samples are drawn from the population is called Sampling method.
Sampling method is classified as either random/probability or non-
random/non-probability. Random/probability sampling method is a
sampling scheme whereby every item/member/element in the population
has a known non-zero chance or probability of being selected in the sample.
The selection of sample items is independent of the person making the
study. Whereas, non-random/non-probability sampling method is the one
which does not provide every item in the population with a known chance of
being selected in the sample. That is, members are selected from the
population in some non-random manner such as convenience or judgment.
The advantage of probability sampling is that sampling error can be
calculated. Sampling error is the degree to which a sample statistic might
differ from the population parameter. When inferring to the population,
results are reported plus or minus the sampling error. In non-probability
sampling, the degree to which the sample differs from the population
remains unknown

10. Probability Sampling Method
10
1. Simple Random Sampling: This is a sampling method where the sample
are selected in such a way that every item in the population has an equal
and known chance of being selected/included in the sample. Simple random
sample could be with replacement or without replacement. The samples
selected randomly are called random samples. It is the purest form of
probability sampling. Random sample can be generally done in a number of
ways such as lottery method, casting of die, tossing of coin and use of
random number table.
Example of simple random sampling of 10 households from a list of 40
households
We have a list of 40 heads of households. Each has a unique number, 1
through 40. We want to select 10 households randomly from this list. Using
a random number table, we select consecutive 2-digit numbers starting from
the upper left. If a random number matches a household's number, that
household is added to the list of selected households. If a random number
does not match a household's number (for example, if it is greater than 40), then
it does not select a household. After each random number is used, it is crossed
out so that it is never used again. We continue to select households until we
have 10.

11. Example of Simple Random Sample
11

12. Example of systematic random sampling of 10 households from a list of 40
households
We first calculate the sampling interval by dividing the total number of
households in the population (40) by the number we want in the sample (10).
In this case, the sampling is interval 4. We then select a number between 1
and the sampling interval from the random number table (in this case 3).
Household #3 is the first household. We then count down the list starting
with household #3 and select each 4th household. For example, the second
selected household is 3 + 4, or #7. Note that when you reach the end of the
list, you should have selected your desired number of households. If you have
not, you have counted wrong or miscalculated the sampling
2. Systematic Sampling: This method is often used instead of simple random
sampling when the complete list of the population is available. This sampling
method involves selection of every kth item from the list after the first has
been randomly selected. The first randomly selected sample is called random
start and it is denoted by 𝑟 while the value 𝑘 = 𝑁/𝑛 is called the sampling
interval. The random start is selected such that1 ≤ 𝑟 < 𝑘. The only advantage
of this method over the simple random sampling technique is its simplicity.
14
12
Probability Sampling Method

13. Systematic Sampling Example
13

14. 3. Stratified Sampling: This is the sampling method that is commonly used
when the population is heterogeneous. In this case, the population is first
divided into homogeneous groups, units, classes called STRATA in such a
manner that all the items in any particular group are similar with regards to
the characteristics under consideration. This sampling method is superior to
random sampling because it reduces sampling error. Examples of stratums
might be males and females (as shown below), or managers and non-
managers. The researcher first identifies the relevant stratums and their
actual representation in the population. Random sampling is then used to
select a sufficient number of subjects from each stratum. "Sufficient" refers to
a sample size large enough for us to be reasonably confident that the stratum
represents the population. The number of sample taken from each stratum is
most often done in proportional to size of the stratum.
14
14
Probability Sampling Method

15. For the proportional allocation of the sample size, the following formula is used:
𝒏𝒉 =
𝒏
𝑵
𝑵𝒉 𝒐𝒓 𝒏 𝑾𝒉 , where 𝒏𝒉= sample size in stratum 𝒉, 𝑵𝒉= Population size in stratum 𝒉, 𝑵 =
𝑵𝒉 = Population size and 𝒏 = 𝒏𝒉= sample size.
Example: If 𝑵 = 𝟏𝟎𝟎𝟎, 𝒏 = 𝟑𝟎𝟎, use the information contained in the table to select sample size
in each stratum proportional to the size of the stratum
14
15
Example of Stratified Sampling
Strat
um 𝑵𝒉
𝒏𝒉
1 205 62
2 234 70
3 148 44
4 220 66
5 193 58
Total 300
𝑛1 = 300 × 205 1000 = 62
𝑛2 = 300 × 234 1000 = 70
𝑛3 = 300 × 148 1000 = 44
𝑛4 = 300 × 220 1000 = 66
𝑛5 = 300 × 193 1000 = 58

16. 4. Cluster sampling: This is a sampling method whereby the entire
population is divided into sections commonly called clusters and randomly
select some of the clusters and then choose all members from selected
clusters. The primary sampling unit is no longer the individual but a group of
individual. For example, an investigator wishing to study students might
first sample groups or clusters of students such as classes or dormitories, and
then select the final sample of students from among the clusters, in this case
classes or dormitories. Although, It is similar to stratified sampling however
it is important to note that unlike strata in stratified sampling, a cluster
should be as heterogeneous as the population itself. Strata and clusters are
both non-overlapping subsets of the population, they differ in several ways.
All strata are represented in the sample, but only subsets of clusters are in
the sample. With stratified sampling, the best survey results occur when
elements within strata are internally homogeneous. However, with cluster
sampling, the best results occur when elements within clusters are internally
heterogeneous.
14
16
Probability Sampling Method

17. Illustration of cluster sampling scheme is as shown in the figures below;
14
17
Example of Cluster Sampling
There are four
clusters in the
population.
The clusters with
blue colour are
selected by simple
random sampling.
All individuals
within the
selected clusters
are enumerated

18. 5. Multistage sampling: It is a combination of random, systematic, stratified,
and cluster sampling. If the probability is involved at each stage, then the
distribution sample statistics can be obtained. It is a complex form of cluster
sampling in which two or more levels of units are embedded one in the other.
 First stage, random number of districts chosen in all states
 Followed by random number of villages/towns/settlements
 Then third stage units will be houses
 All ultimate units (houses, for instance) selected at last step are surveyed
This technique is essentially the process of taking random samples of
preceding random samples. It is not as effective as true random sampling, but
probably solves more of the problems inherent to random sampling. It is an
effective strategy because it banks on multiple randomizations.
14
18
Probability Sampling Method

19. 1. Convenience Sampling: As the name implies, the sample is selected because
they are convenient i.e. use who is available. It is also known as grab or
opportunity sampling or accidental or haphazard sampling. It involves the
sample being drawn from that part of the population which is close to hand. This
non-probability method is often used during preliminary research efforts to get a
gross estimate of the results, without incurring the cost or time required to select
a random sample.
2. Purposive or Judgment Sampling: This is a common non-probability method of
sampling. The researcher selects the sample based on preconceived purpose or on
the judgment of the investigator. This is usually an extension of convenience
sampling. For example, a researcher may decide to draw the entire sample from
one "representative" city, even though the population includes all cities. When
using this method, the researcher must be confident that the chosen sample is
truly representative of the entire population. This is used primarily when there is
a limited number of people that have expertise in the area being researched.
3. Quota Sampling: This is the non-probability equivalent of stratified sampling.
Like stratified sampling, the researcher first identifies the stratums and their
proportions as they are represented in the population. Then convenience or
judgment sampling is used to select the required number of subjects from each
stratum. This differs from stratified sampling, where the stratums are filled by
random sampling.
14
19
Non-Probability Sampling Method