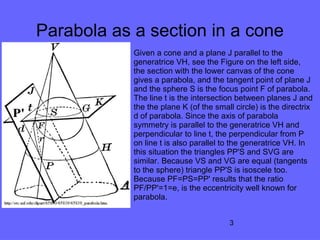
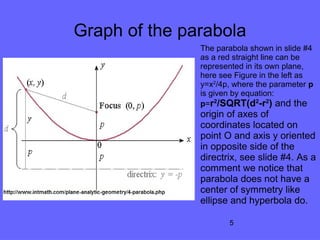
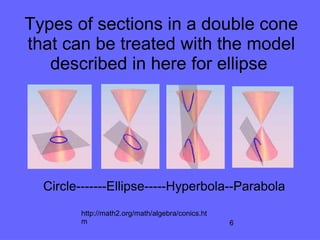
The document discusses the geometric properties of a parabola, including its formation through sections of a cone and its focus and directrix. It highlights the use of Dandelin spheres and synthetic geometry to derive key characteristics of parabolas and compares them with other conic sections. The author concludes that the internet is a valuable resource for understanding these concepts and suggests the same method can be applied to ellipses and hyperbolas.

1. About parabola, an example of
learning shifts on Internet
Danut Dragoi, PhD
California
02/02/2017

2. 2
Dandelin sphere for parabola

3. 3
Parabola as a section in a cone
Given a cone and a plane J parallel to the
generatrice VH, see the Figure on the left side,
the section with the lower canvas of the cone
gives a parabola, and the tangent point of plane J
and the sphere S is the focus point F of parabola.
The line t is the intersection between planes J and
the the plane K (of the small circle) is the directrix
d of parabola. Since the axis of parabola
symmetry is parallel to the generatrice VH and
perpendicular to line t, the perpendicular from P
on line t is also parallel to the generatrice VH. In
this situation the triangles PP'S and SVG are
similar. Because VS and VG are equal (tangents
to the sphere) triangle PP'S is isoscele too.
Because PF=PS=PP' results that the ratio
PF/PP'=1=e, is the eccentricity well known for
parabola.

4. 4
Direct calculation of the focus and
the position of the directrix
Figure on the left represents the main
section of the cone in slide #3. From
simple synthetic geometry we can
derive the focus F of parabola,
TO2
=VT*WT and VT is given by:
VT=VF=r2
/SQRT(d2
-r2
), where r is the
radius of the Dandelin sphere and d
the distance between the tip W of the
cone and the center of the sphere.
The directrix is located on point D
with VD=r2
/SQRT(d2
-r2
). As a
comment this result can be predicted
from hyperbola results where one
sphere radius becomes zero and the
eccentricity transforms in 1.

5. 5
Graph of the parabola
The parabola shown in slide #4
as a red straight line can be
represented in its own plane,
here see Figure in the left as
y=x2
/4p, where the parameter p
is given by equation:
p=r2
/SQRT(d2
-r2
) and the
origin of axes of
coordinates located on
point O and axis y oriented
in opposite side of the
directrix, see slide #4. As a
comment we notice that
parabola does not have a
center of symmetry like
ellipse and hyperbola do.

6. 6
Types of sections in a double cone
that can be treated with the model
described in here for ellipse
Circle-------Ellipse-----Hyperbola--Parabola
http://math2.org/math/algebra/conics.ht
m

7. 7
Conclusion

Using the learning shifts suggested in a
previous posting, link below,
the Internet is found very helpful on fully
describing the parabola utilizing the synthetic
geometry in space and plane.

The method shown could be applied easily to
other conics such as ellipse, and hyperbola.
https://www.linkedin.com/pulse/learning-shifts-internet-era-danut-dragoi?trk=mp-reader-
card