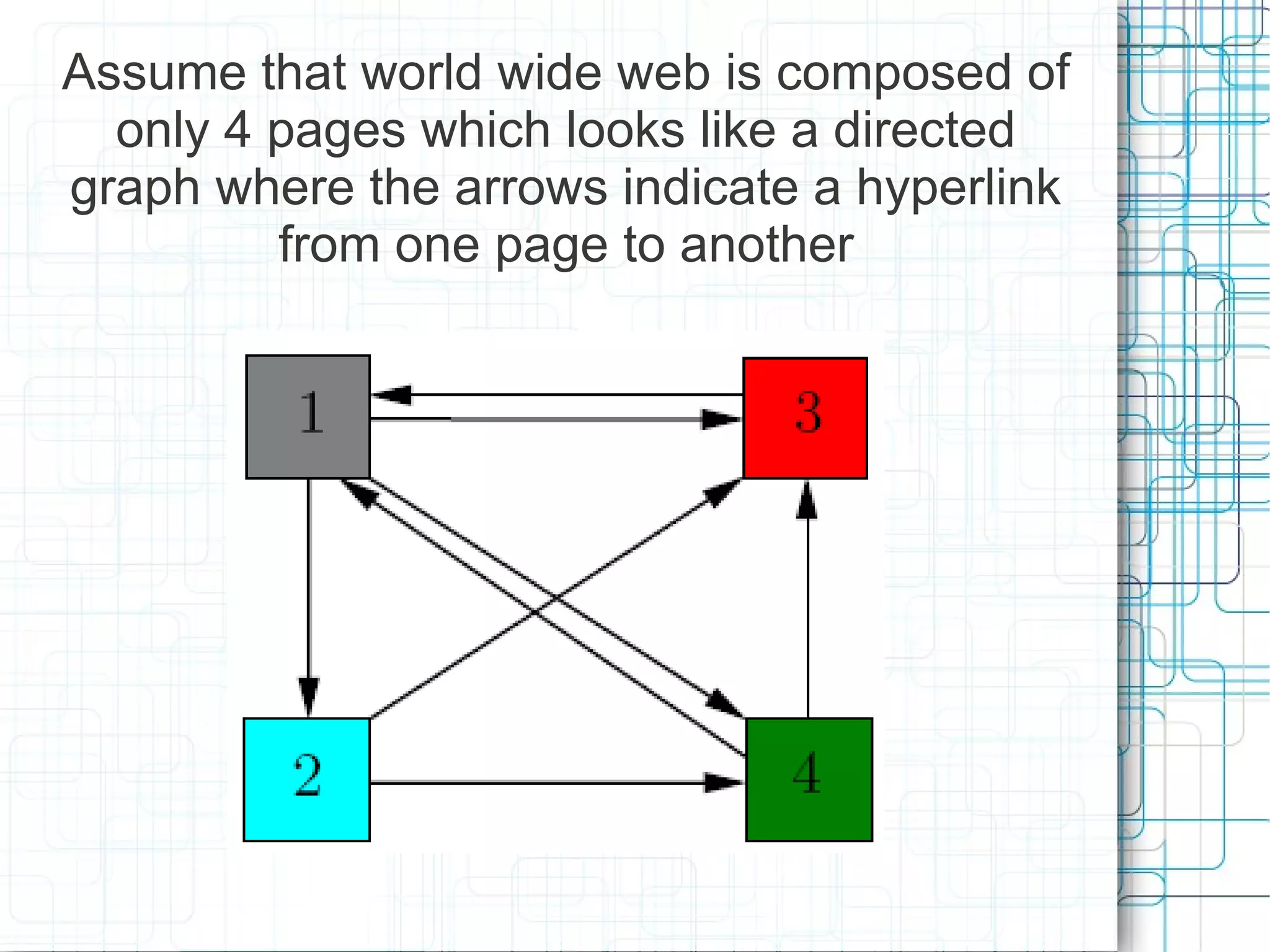
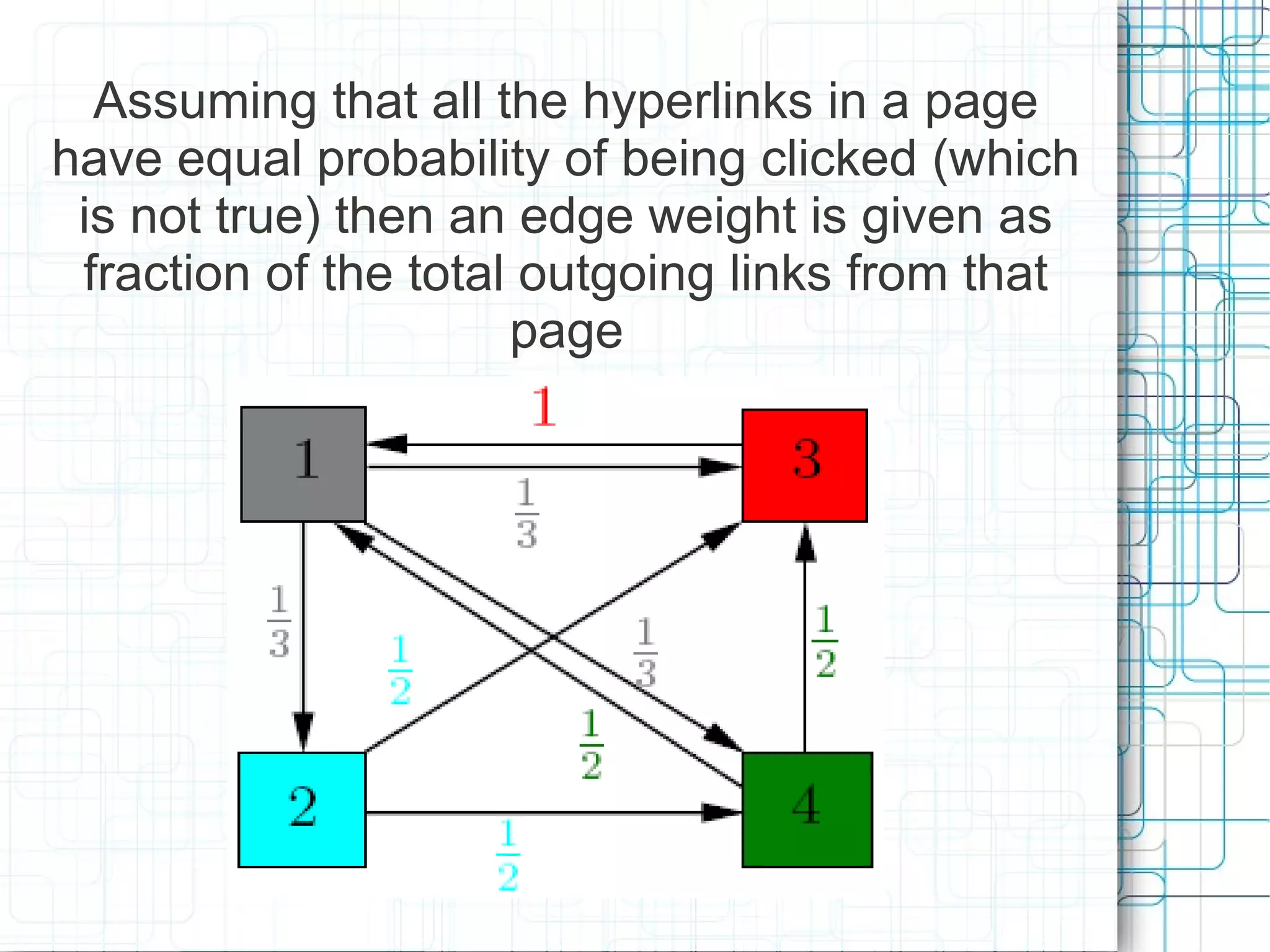
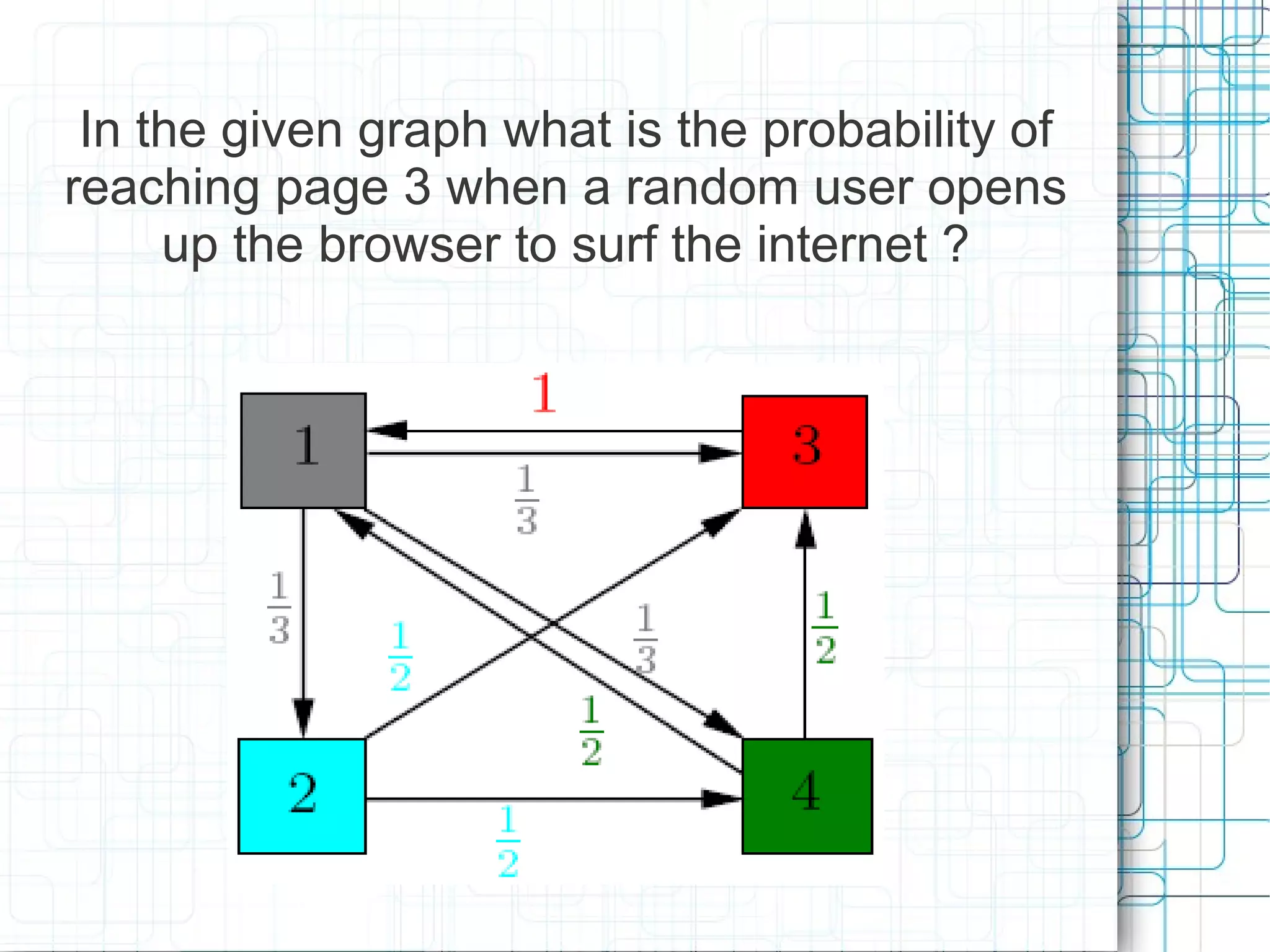
PageRank is an algorithm created by Google's founders to rank the importance of websites in the network of links on the internet. It uses a probability-based model to determine the likelihood that a random user would arrive at a given page. PageRank is calculated through an iterative process of evaluating the inbound links from other pages, with more weight given to pages that are already highly ranked. The example demonstrates how PageRank is computed for a simple network of four pages, with the highest ranking going to the page that receives a link from the page with the strongest inbound links.

1. Google PageRank
By
Abhijit Mondal
Software Engineer
HolidayIQ.com

2. What is PageRank ?
It's the algorithm developed by Google
founders Larry 'Page' and Sergey Brin to
quantify the importance of a 'page' or website
in the complex network of the world wide web

3. PageRank is only a criteria and not the only
criteria by which Google decides where your
page or website will rank in the search results

4. From the inception of PageRank, the search
results ranking algorithms have developed so
much that at this moment nobody knows what
is the exact algorithm (algorithms) Google
uses to rank search results.
If it was known there would be no need for
SEO experts

5. Assume that world wide web is composed of
only 4 pages which looks like a directed
graph where the arrows indicate a hyperlink
from one page to another

6. Assuming that all the hyperlinks in a page
have equal probability of being clicked (which
is not true) then an edge weight is given as
fraction of the total outgoing links from that
page

7. Loosely speaking PageRank of a page A is a
direct measure of the probability of visiting
page A when a random user opens up a
browser and follows some hyperlinks to reach
page A

8. In the given graph what is the probability of
reaching page 3 when a random user opens
up the browser to surf the internet ?

9. How can the user reach page 3 ?
He is on page 1 then clicks link of page 3
Or
He is on page 2 then clicks link of page 3
Or
He is on page 4 then clicks link of page 3
Or
Directly types url of page 3

10. Denoting the probability of reaching page i as
P(i), then
P(3) = (1-d) x (P(1)x(1/3) + P(2)x(1/2) + P(4)x(1/2)) + d x (1/4)
This formula follows from the laws of
probability
Where 'd' is the probability that user directly
visits a page, hence (1-d) is the probability
that user comes through a different page.

11. … Similarly the equations for P(1), P(2) and
P(4) are
P(1) = (1-d) x (P(3) + P(4)x(1/2)) + d x (1/4)
P(2) = (1-d) x (P(1)x(1/3)) + d x (1/4)
P(4) = (1-d) x (P(2)x(1/2) + P(1)x(1/3)) + d x (1/4)
But we now have a problem, if we already do not know
what is P(1) and we need P(3) to compute it, then how
can P(3) be computed using P(1) ???
These are coupled equations and solved using Matrices
(eigenvalues and eigenvectors) or more simply using
repeated iterations till the values converge

12. But why calculates probabilities when we
want PageRank ? Because the probability of
reaching page i is the direct measure of the
PageRank of i. Letting PR(i) = P(i) where
PR(i) is the PageRank of page i.
Denoting PRk(i) as the PageRank computed
using the earlier formula in the kth iteration, in
the (k+1)th iteration ...

13. PRk+1(3) = (1-d) x (PRk(1)x(1/3) + PRk(2)x(1/2) +
PRk(4)x(1/2)) + d x (1/4)
PRk+1(1) = (1-d) x (PRk(3) + PRk(4)x(1/2)) + d x (1/4)
PRk+1(2) = (1-d) x (PRk(1)x(1/3)) + d x (1/4)
PRk+1(4) = (1-d) x (PRk(2)x(1/2) + PRk(1)x(1/3)) + d x
(1/4)
Letting d=0.15 and
PR0(1) = PR0(2) = PR0(3) = PR0(4) = 0.25
Compute PRk(i) for each k until |PRk+1(i) – PRk(i)| < ɛ for
all i =1, 2, 3, 4, where ɛ is some very small real number

14. Computing the PageRanks of each page
using the above formula:
PR(1) = 0.368
PR(2) = 0.142
PR(3) = 0.288
PR(4) = 0.202
Thus page 1 is the page with highest
PageRank. Surprising since page 3 receives
the most backlinks (from 1, 2 and 4), but 1
receives backlink from 3 and page 3 only
gives backlink to page 1, thus 'informing' that
page 1 is really important

15. What are the conclusions from the above
results ?
More number of backlinks, better PageRank
Backlinks from pages with high PageRanks
themselves improves my PageRank
If there are good many backlinks from
Wikipedia or some university website like
iitk.ac.in to my site HolidayIQ.com then my
PageRank will always improve