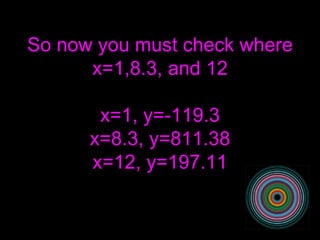Costco is looking to negotiate a new contract with the makers of Otter Pops. Based on past sales data modeled by an equation, approximately 5,384 boxes of Otter Pops could potentially be sold per year. If sold at $9.49 per box, this would result in total sales of $51,094.16. However, the Otter Pop company offers bulk discounts. For Costco to earn at least a 10% profit per box, they need to purchase orders of at least 678 boxes, which based on modeling months of highest sales, would be between June and October. August was identified as the month with the largest predicted sales.

1. Otter Pop Frenzy By Karly Kelso

2. Costco is revamping their computer programs, but their system is currently shut down.

3. They need to negotiate a new contract with the makers of Otter Pops immediately, and they only have a few random graphs with equations from a previous presentation to look at.

4. If Otter Pops were sold year round, the amount of people buying them can be shown as y(t)=-2.413x ³ +24.715x ² +86.307x-227.867 where t is the month and t=1 is January

5. How many Otter Pops could potentially be sold?

6. ANSWER The way to figure out this answer is to look at the area under the curve or the integral of the equation.

7. If you take the integral of y(t)=-2.413x ³ +24.715x ² +86.307x-227.867 You get: -.603x 4 +8.238x ³ +43.154x ² -227.867x │ from 1 to 12 plugging in Y(12)-Y(1) gives the answer of approximately 5384 boxes of Otter Pops

8. You can also plug this equation into your calculator and graph it and then hit 2 nd Calc and 7 to calculate the integral from 1 to 12.

9. If sold at $9.49 per box (which happens to be the highest price they can be sold at), how much money would be made if the total potential sold could be reached?

10. ANSWER This problem is a little more simple. You simply multiply the number you reached in part A by 9.49 to get the answer $51,094.16

11. HOWEVER, the Otter Pop company will sell Otter Pops at a lower price when the quantity bought is higher, but the boxes can only be purchased during the month that Costco is planning on selling them…

12. The price of each Otter Pop when bought in a bulk is modeled by the equation y(b)=21.525-1.978lnb where b is the total number purchased and y(b) is the price per Otter Pop box.

13. If 10% profit must be made per box, when can Costco afford to purchase these Otter Pops from the company?

14. ANSWER First you must calculate the highest price that the Otter Pops can be bought at to earn a profit.

15. This amount will be equal to 9.49/1.1 because the general equation is 110% X the price bought=the price sold at. So the price bought=the price sold at/110%(or 1.1) This equals $8.63

16. Now the next trick to solving the equation is to set $8.63 equal to the equation y(b)=21.525-1.978lnb

17. 8.63=21.525-1.978lnb -12.895=-1.978lnb 6.519=lnb e 6.519 =b 678=b

18. This value of b says that Otter Pops must be purchased in orders larger than 678 in order to earn enough profit. Now you must set THIS number equal to y(t)=-2.413x ³ +24.715x ² +86.307x-227.867 to find out which months are profitable

19. It is profitable when the equation is greater than 678 so you set this equation equal to 678 and solve for x.

20. However, an easier way to solve the problem is to graph y(t)=-2.413x ³ +24.715x ² +86.307x-227.867 and y=678 and use your calculator to find the intersection points of these two graphs

21. When you do this, you find that the intersection points are AROUND 6 and 10, meaning that Otter Pops should be sold between June and October in order to make a high enough profit

22. The Otter Pop company also wanted to know for which month they should expect the largest order from Costco

23. For this, you must find the derivative of the original equation

24. Original equation y(t)=-2.413x ³ +24.715x ² +86.307x-227.867 Derivative of equation y’(t)=-7.239x ² +49.43x+86.307

25. The month for the largest amount of Otter Pops sold is a maximum. To find the maximum, check the endpoints, where the derivative equals zero, and where the derivative does not exist.

26. To find where the derivative equals zero, you graph the equation and hit 2 nd calc and 2. This produces an answer of 8.3. Also, the derivative exists everywhere.

27. So now you must check where x=1,8.3, and 12 x=1, y=-119.3 x=8.3, y=811.38 x=12, y=197.11

28. Therefore, 8.3 is a maximum so August is the month where the most number of Otter Pops are sold.