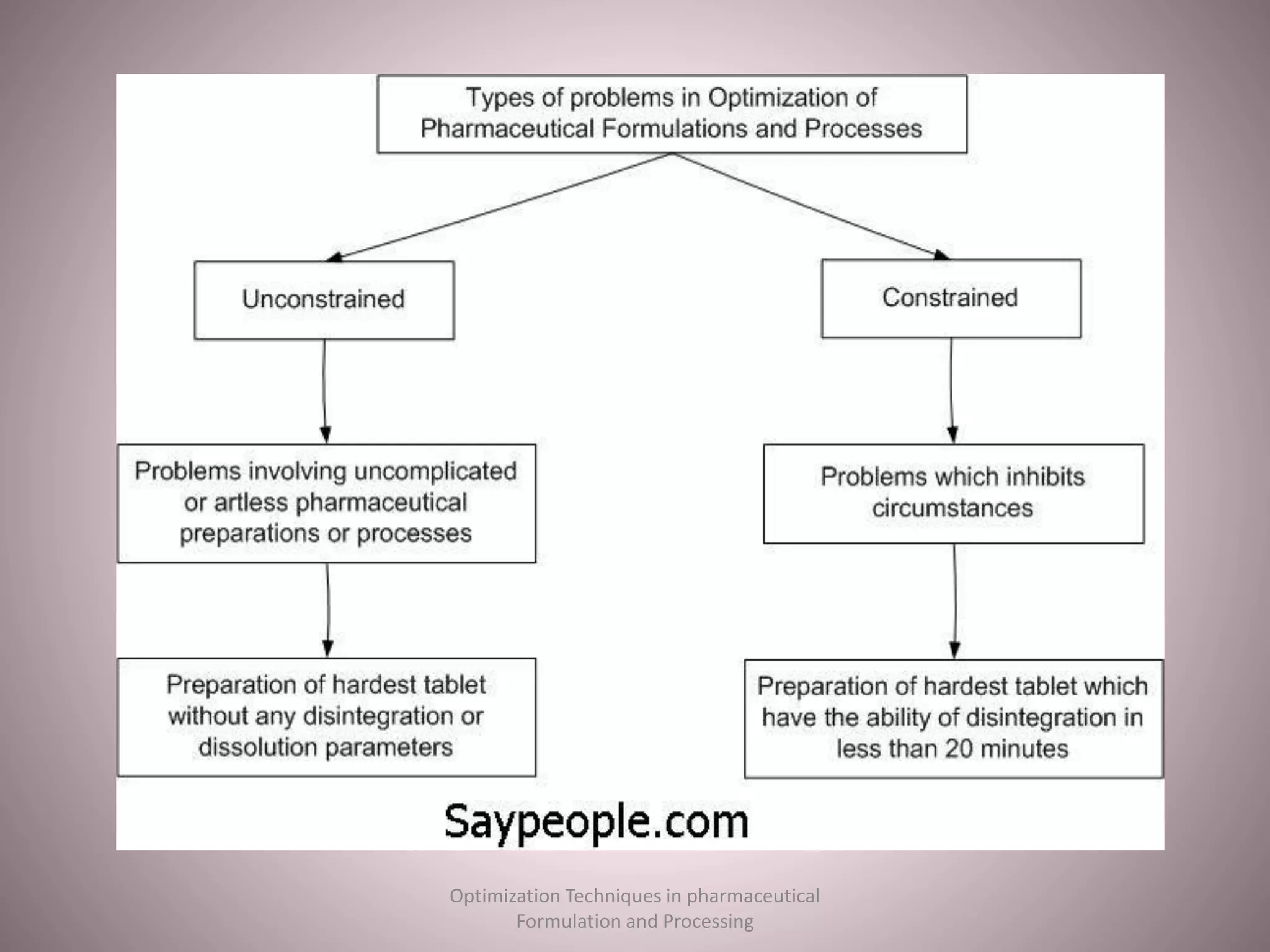
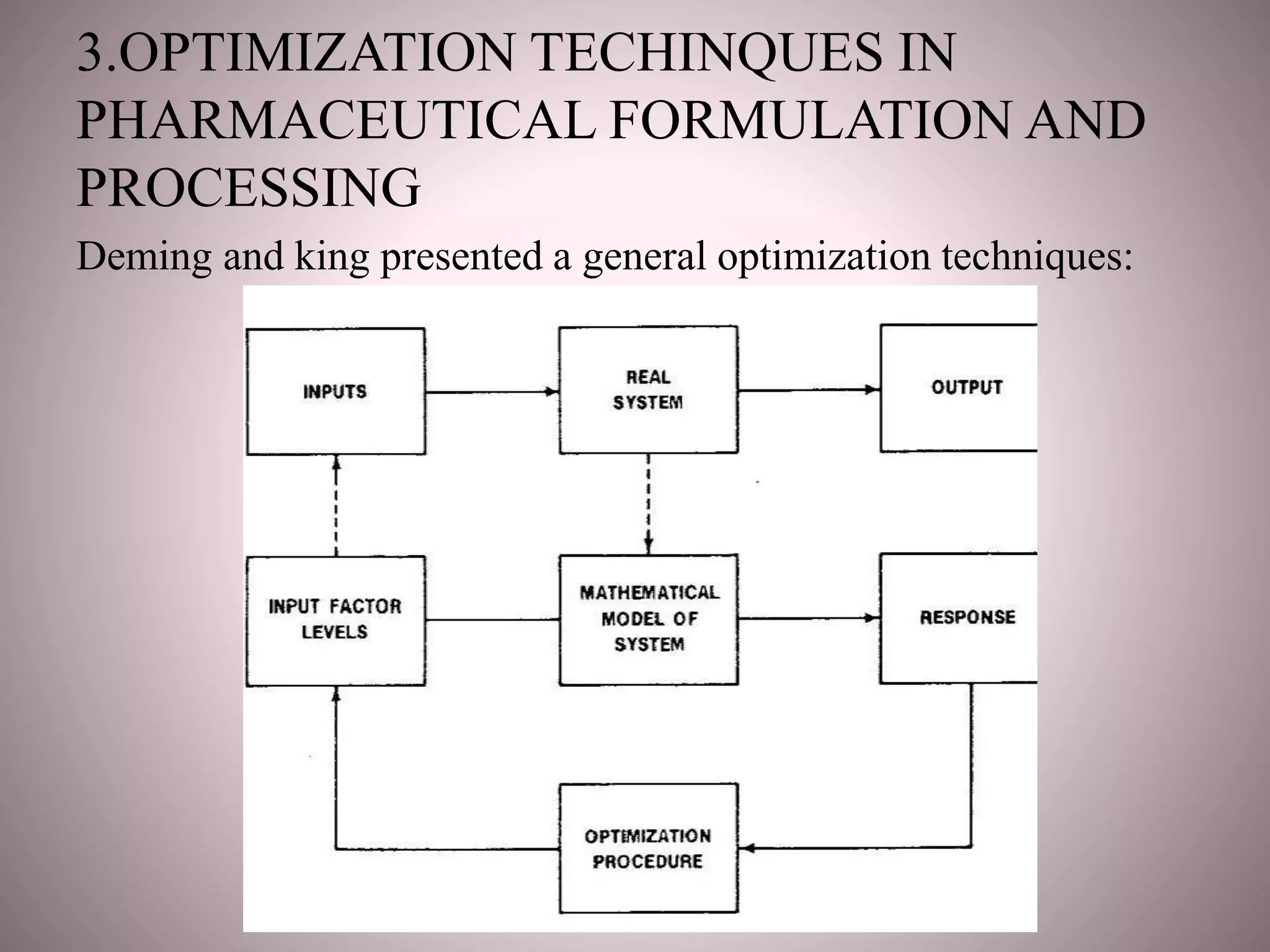
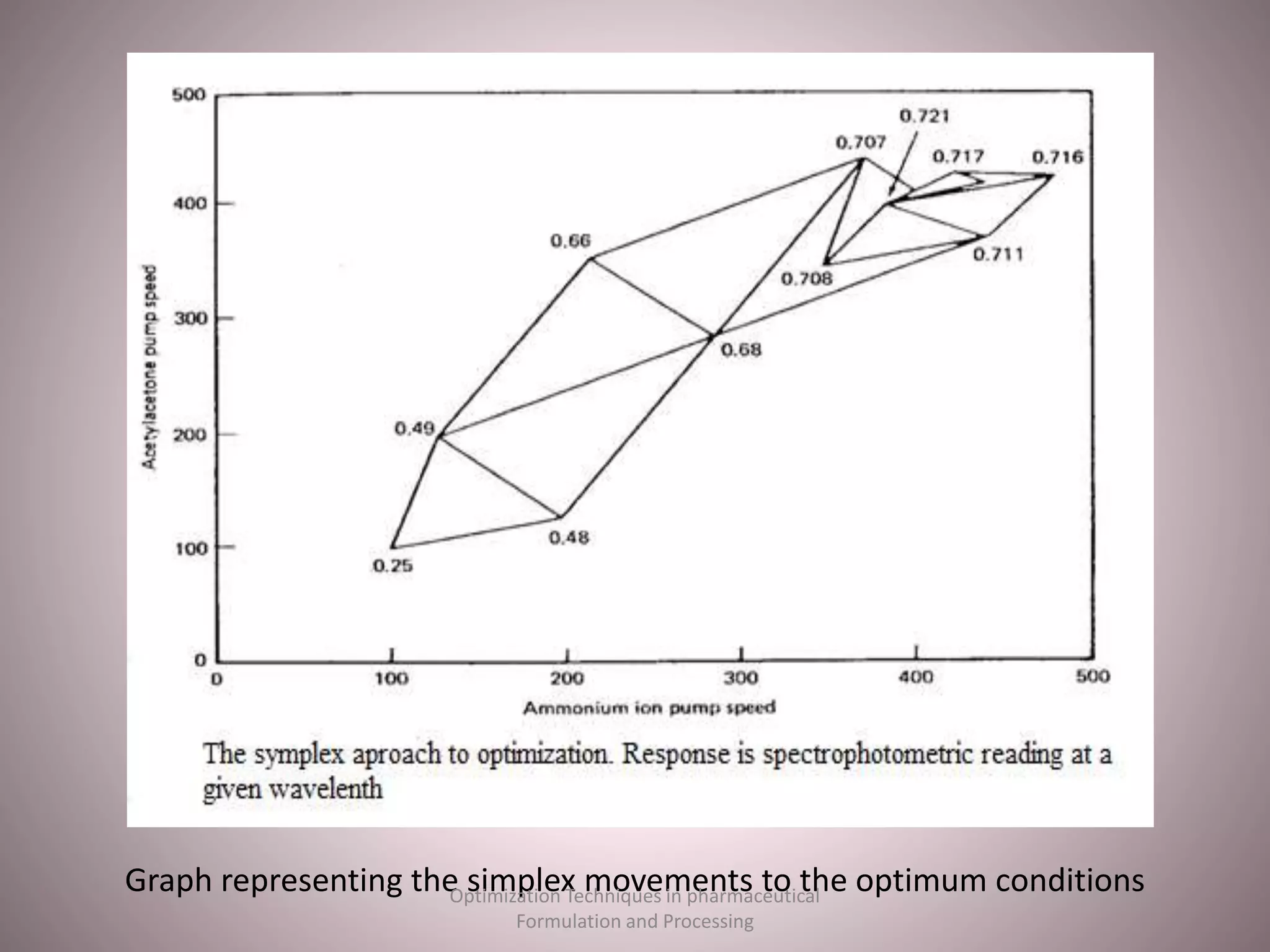
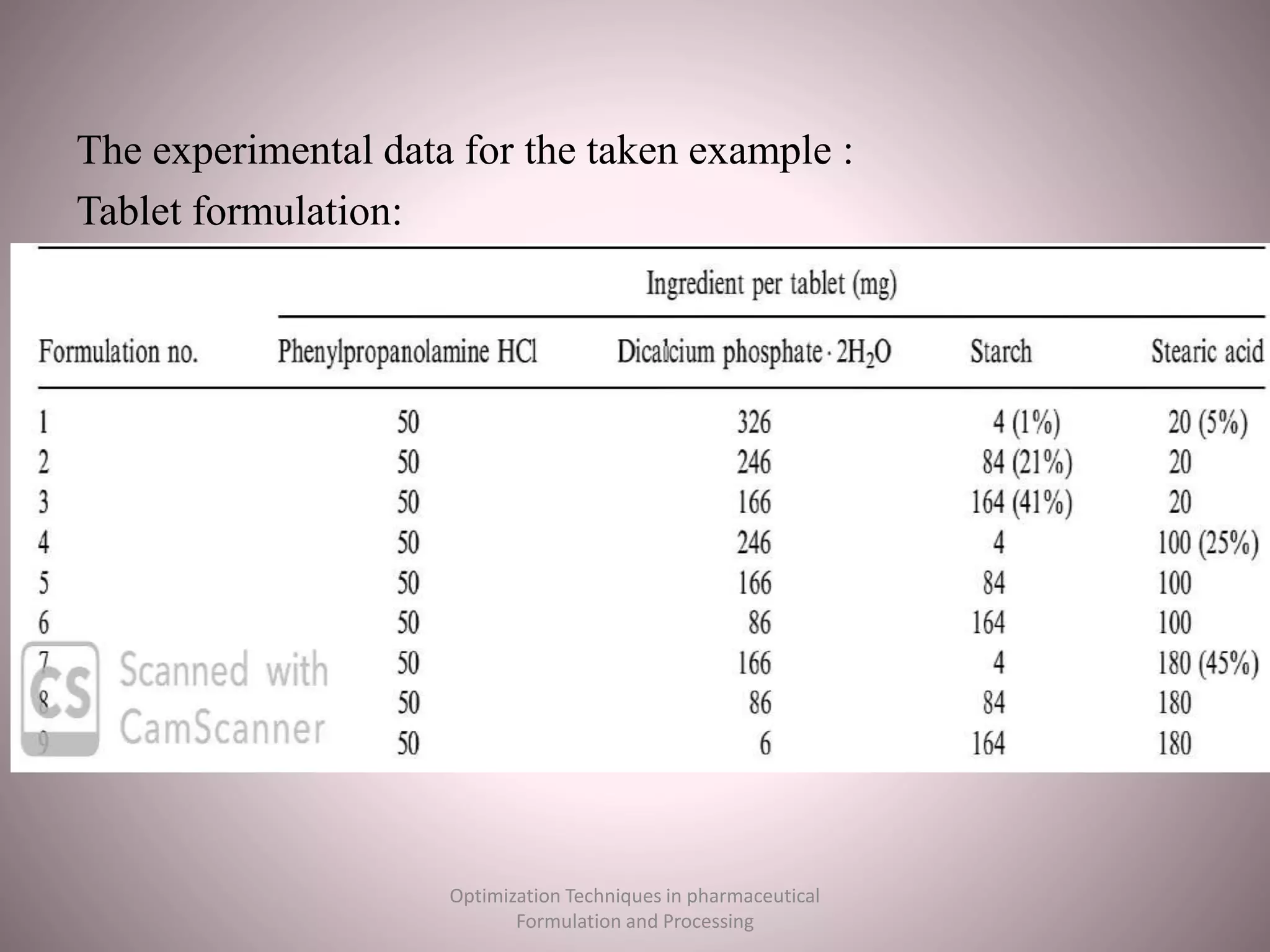
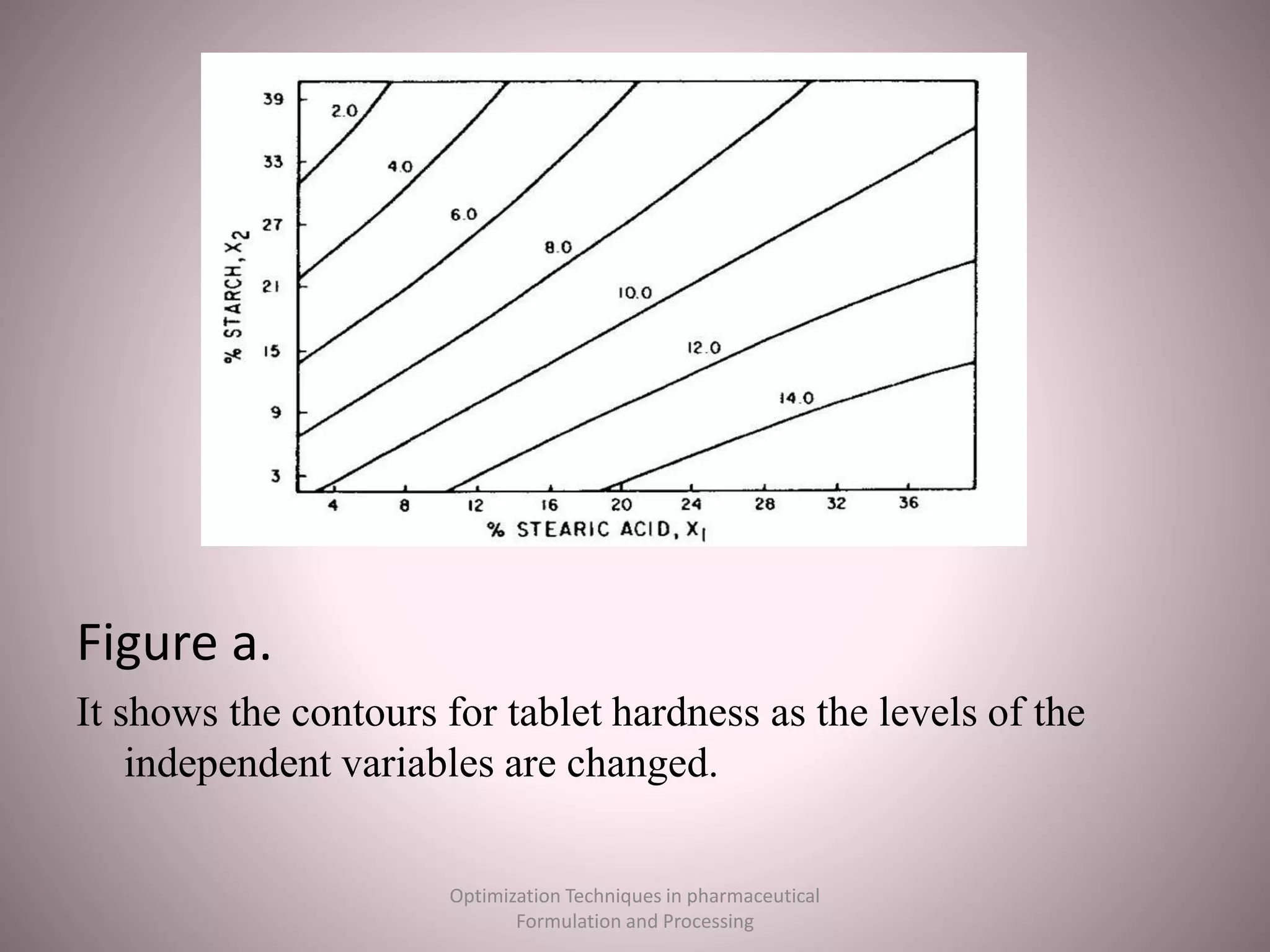
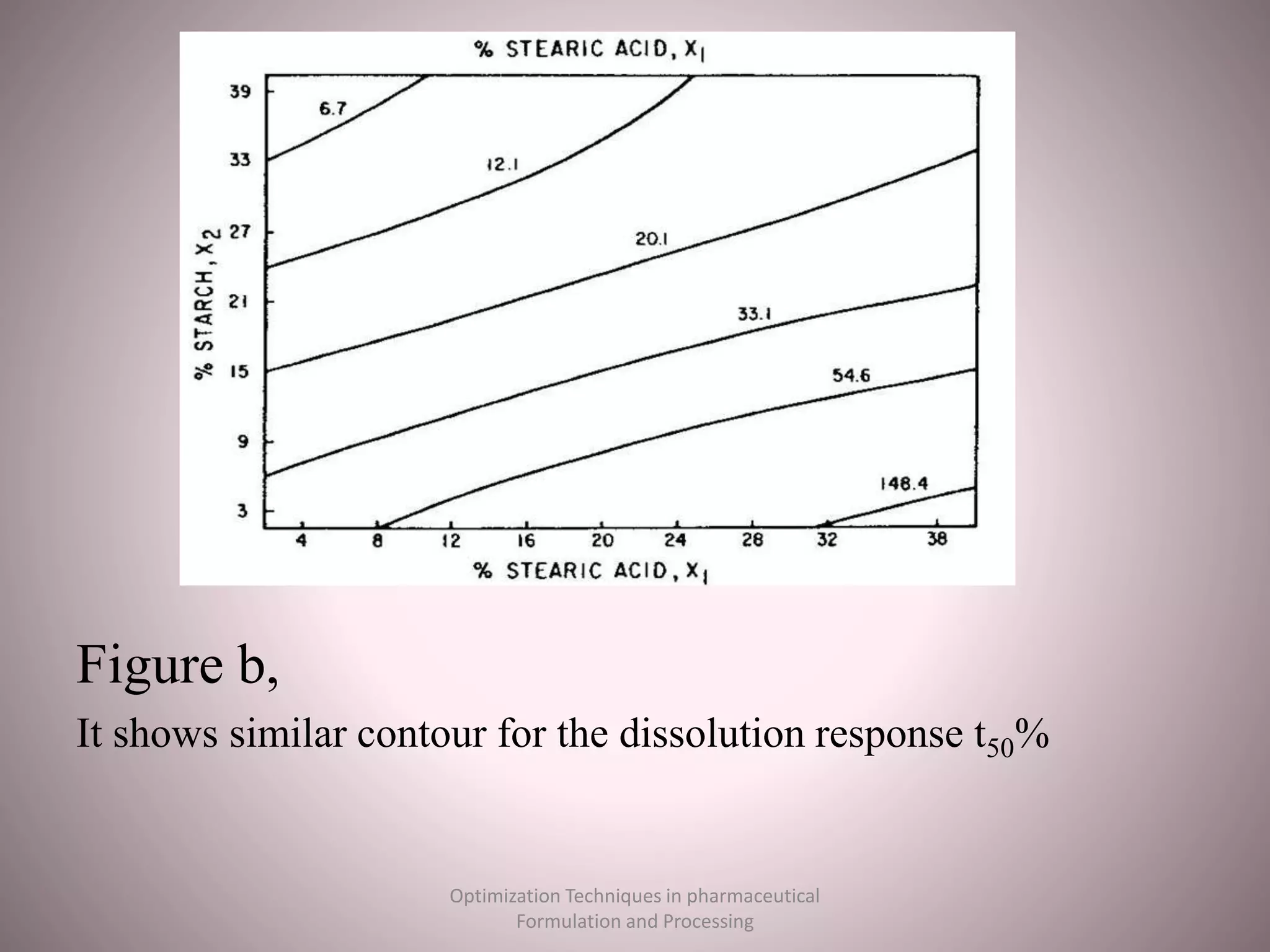
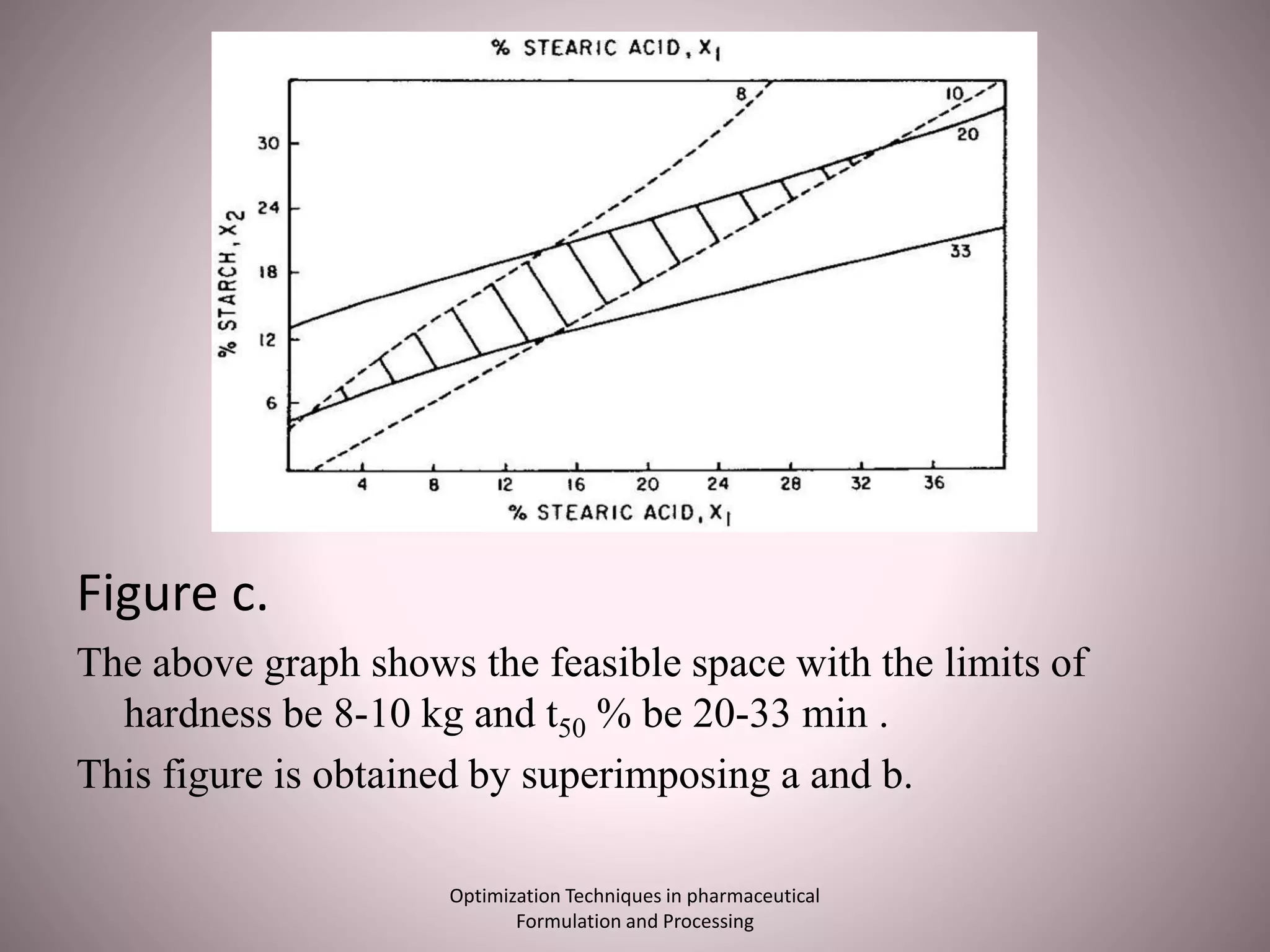
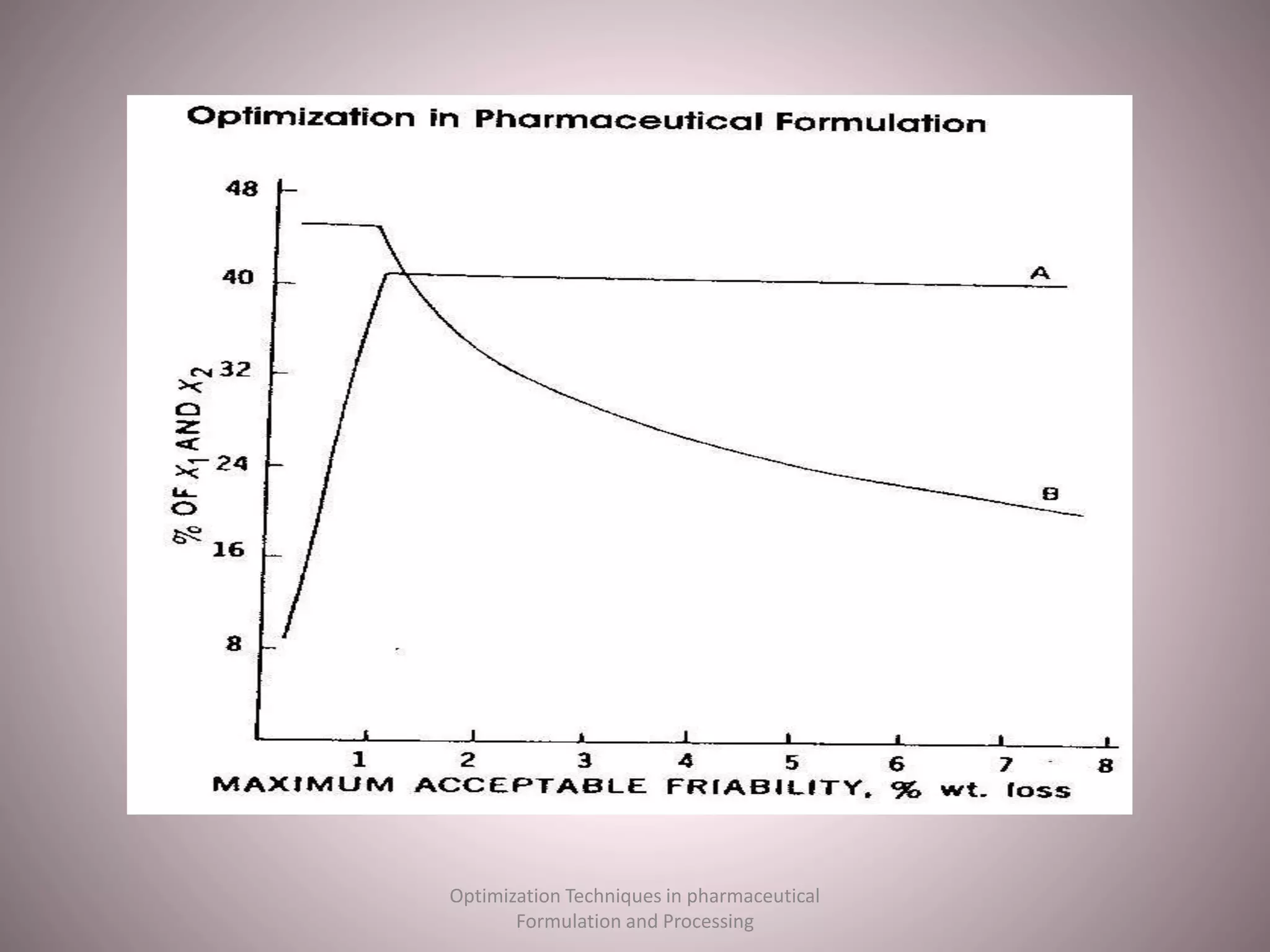
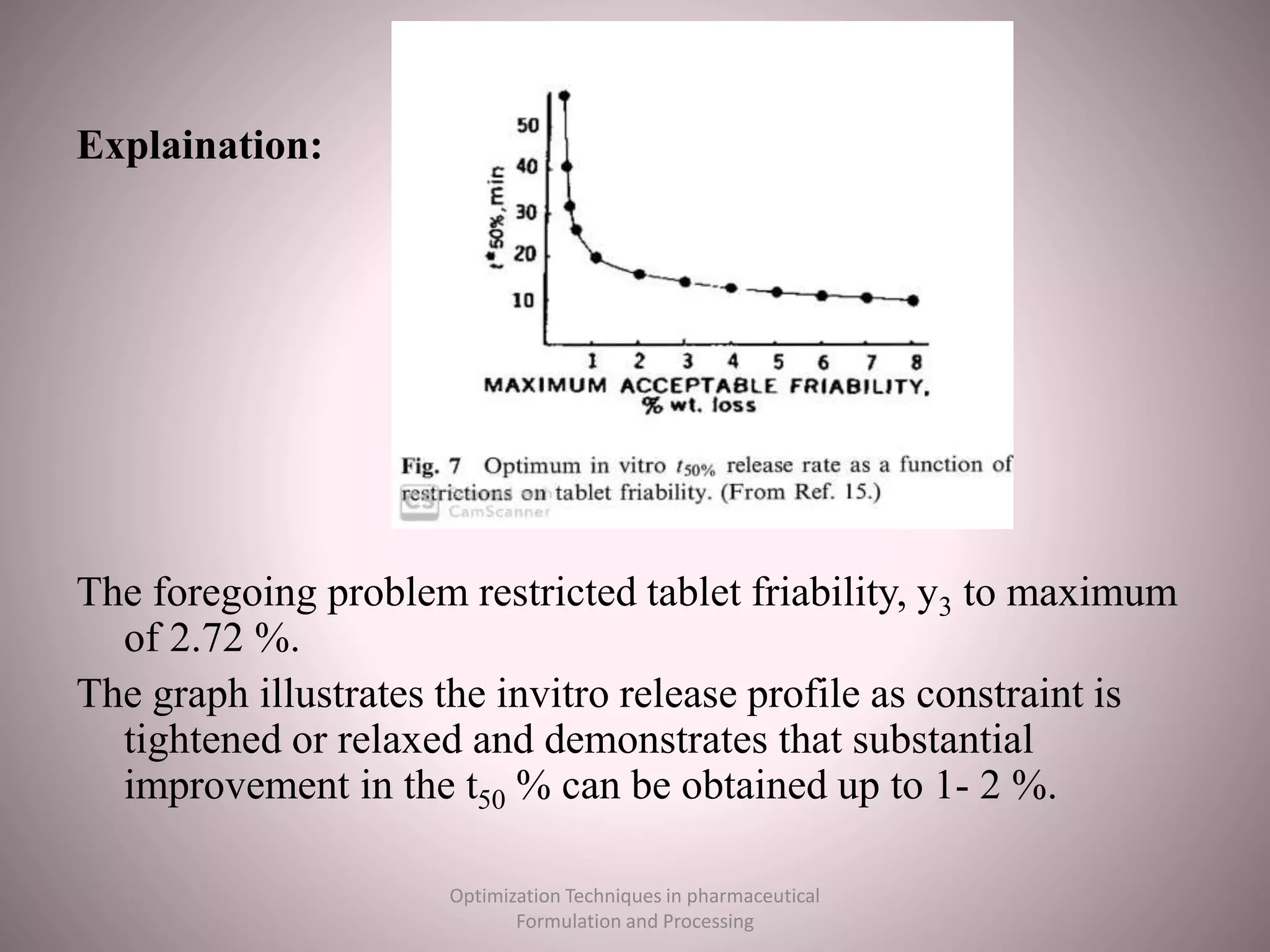
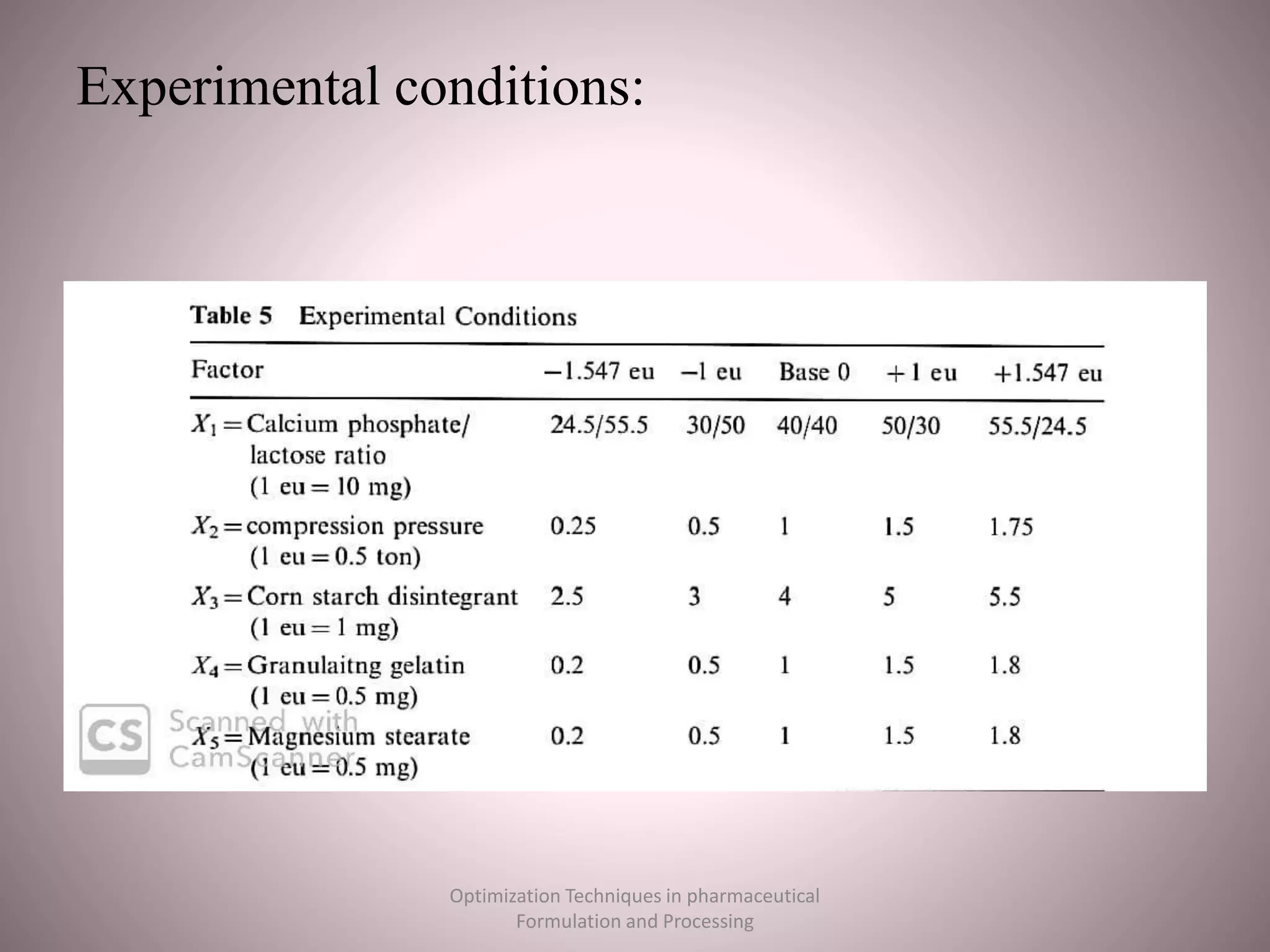
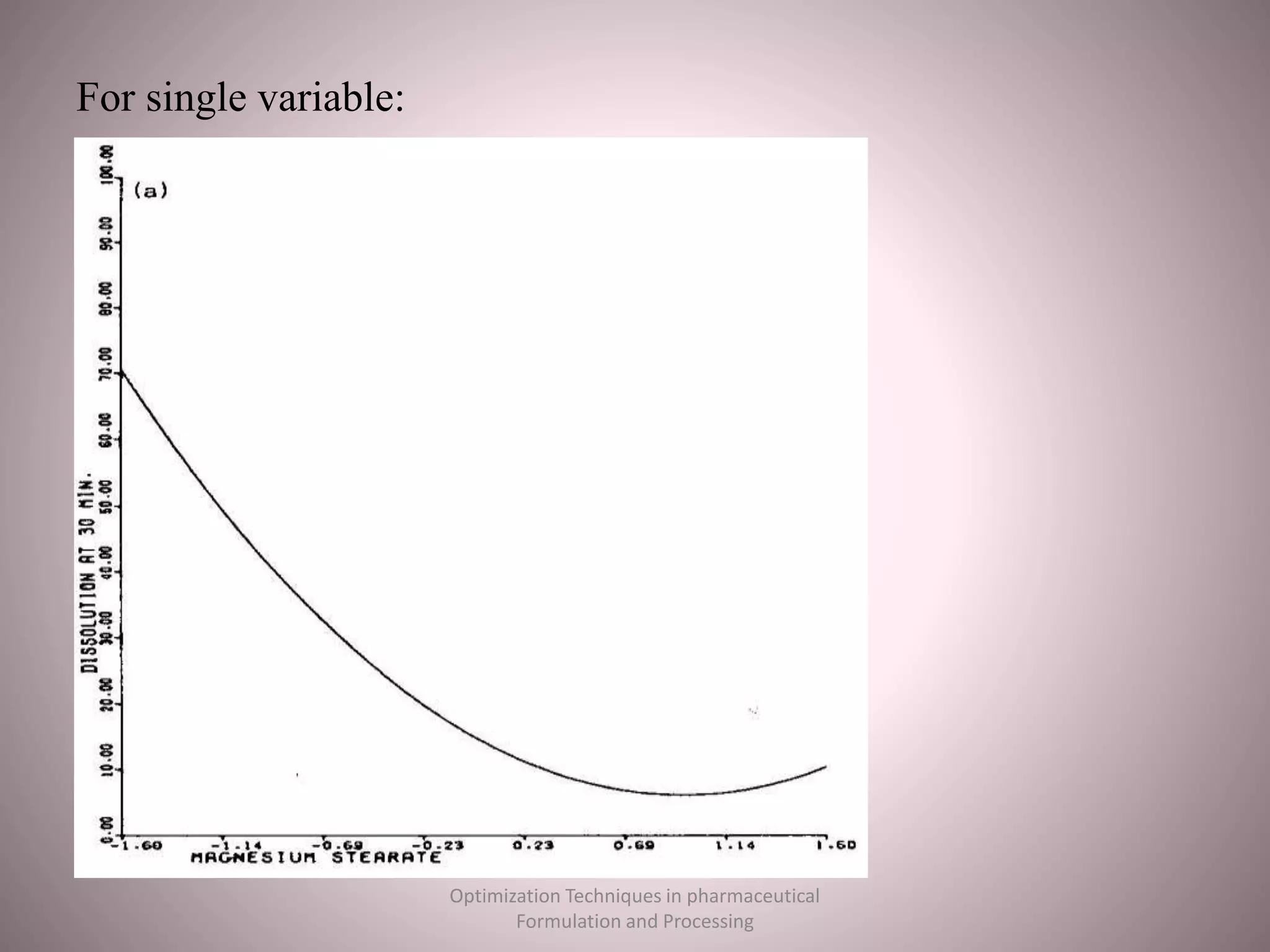
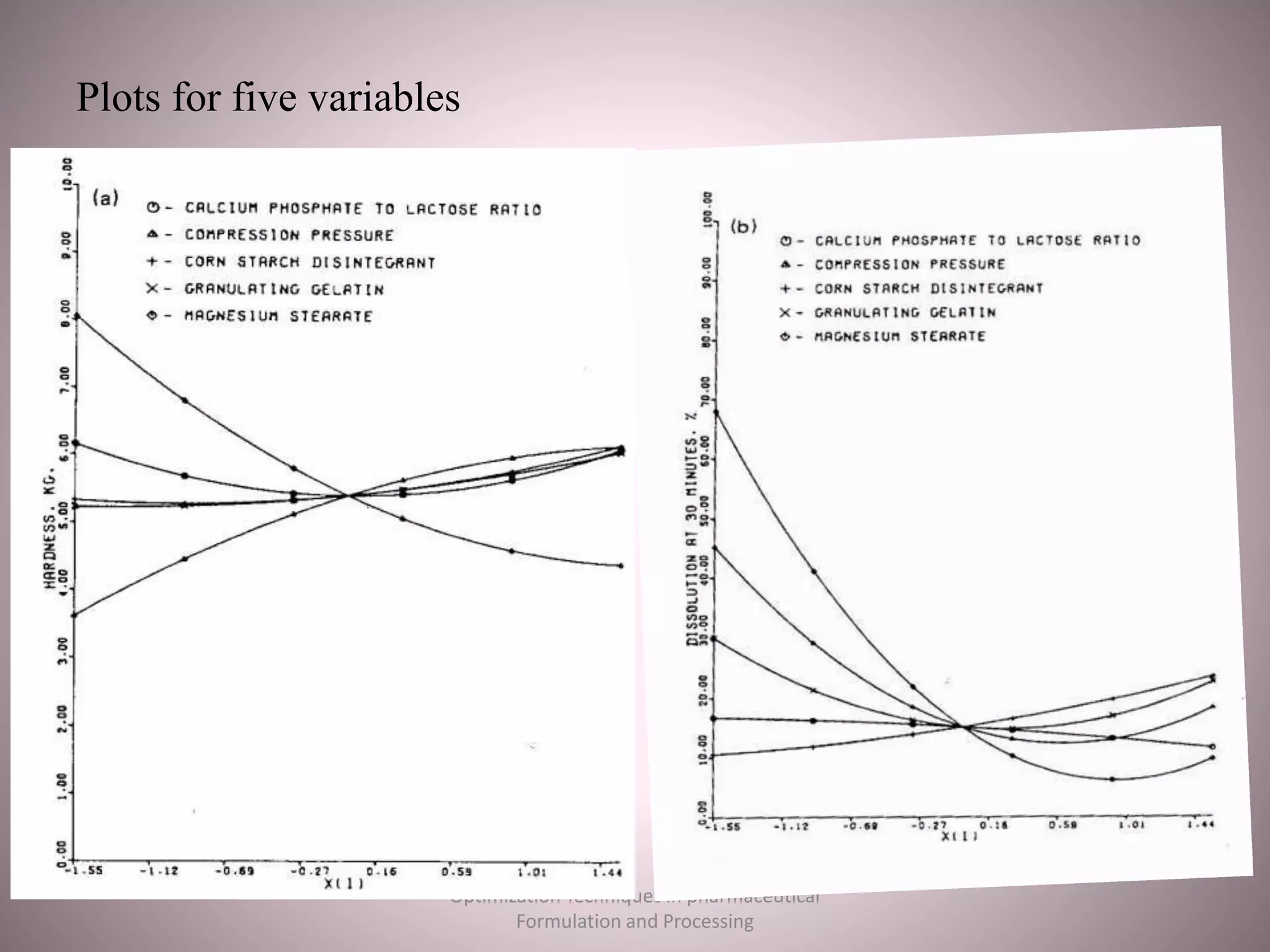
The document discusses optimization techniques used in pharmaceutical formulation and processing. It begins by defining optimization and its importance in developing drug products that meet bioavailability and mass production requirements. The key parameters of optimization include problem type (constrained vs unconstrained), variables (independent vs dependent), and techniques like evolutionary operations, simplex method, and Lagrangian method. Evolutionary operations involve repeated small changes to formulation or process to evolve the optimal product. Simplex method uses geometric shapes to navigate factor settings towards better responses. Lagrangian method applies polynomial models to experimental data to find the optimum based on responses like tablet hardness and friability.