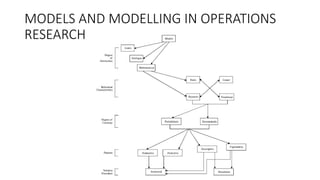
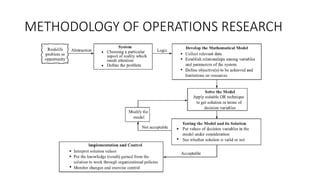
Here are the steps to solve this LP problem using the simplex method: 1) Write the problem in standard form by introducing slack/surplus variables: Maximize Z = 3x1 + 5x2 + 4x3 Subject to: 2x1 + 3x2 + s1 = 8 2x2 + 5x3 - s2 = 10 3x1 + 2x2 + 4x3 - s3 = 15 x1, x2, x3, s1, s2, s3 ≥ 0 2) Initialize the basic feasible solution: Basis: s1, s2, s3 Basic variables: s1 = 8

1. OPERATIONS RESEARCH

2. OPERATIONS RESEARCH – A QUANTITATIVE
PERSPECTIVE TO DECISION-MAKING
• Knowledge, innovations and technology are changing
• hence decision-making in today’s social and business environment has
become a complex task.
• decision-makers cannot afford to make decisions based on their personal
experiences, guesswork or intuition.
• Operations research approach helps in the comparison of all possible
alternatives (courses of action or acts) with respect to their potential
outcomes and then sensitivity analysis of the solution to changes or errors
in numerical values.
• However, this approach (or technique) is an aid to the decision-makers’s
judgement not a substitute for it.

3. THE HISTORY OF OPERATIONS RESEARCH
• World War II
• a particular model and technique of OR can be traced back as early as in
World War I, when Thomas Edison (1914–15) made an effort to use a
tactical game board for finding a solution to minimize shipping losses from
enemy submarines, instead of risking ships in actual war conditions.
• About the same time AK Erlang, a Danish engineer, carried out experiments
to study the fluctuations in demand for telephone facilities using automatic
dialling equipment
• Since World War II involved strategic and tactical problems that were highly
complicated, to expect adequate solutions from individuals or specialists in
a single discipline was unrealistic.

4. THE HISTORY OF OPERATIONS RESEARCH
• specialists in mathematics, economics, statistics and probability
theory, engineering, behavioural, and physical science, were formed
as special units within the armed forces, in order to deal with
strategic and tactical problems of various military operations.
• Such groups were first formed by the British Air Force and later the
American armed forces formed similar groups. One of the groups in
Britain came to be known as Blackett’s Circus. This group, under the
leadership of Prof. P M S Blackett was attached to the Radar
Operational Research unit and was assigned the problem of analyzing
the coordination of radar equipment at gun sites. Following the
success of this group similar mixed-team approach was also adopted
in other allied nations.

5. DEFINITIONS OF OPERATIONS RESEARCH
• Operations research is the application of the methods of science to
complex problems in the direction and management of large systems of
men, machines, materials and money in industry, business, government
and defence. The distinctive approach is to develop a scientific model of
the system incorporating measurements of factors such as chance and risk,
with which to predict and compare the outcomes of alternative decisions,
strategies or controls. The purpose is to help management in determining
its policy and actions scientifically (Operational Research Society, UK)
• The application of the scientific method to the study of operations of large
complex organizations or activities. It provides top level administrators
with a quantitative basis for decisions that will increase the effectiveness of
such organizations in carrying out their basic purposes. (Committee on OR
National Research Council, USA)

6. DEFINITIONS OF OPERATIONS RESEARCH
• Operations research is the systematic application of quantitative
methods, techniques and tools to the analysis of problems involving
the operation of systems. (Daellenbach and George, 1978)

7. FEATURES OF OPERATIONS RESEARCH
APPROACH
• Interdisciplinary approach
• Scientific approach
• Holistic approach
• Objective-oriented approach

8. MODELS AND MODELLING IN OPERATIONS
RESEARCH

9. METHODS FOR SOLVING OPERATIONS
RESEARCH MODELS
• Analytical (or deductive) method: In this method, classical
optimization techniques such as calculus, finite difference and graphs
are used for solving an OR model. The analytical methods are
noniterative methods to obtain an optimal solution of a problem
• Numerical (or iterative) method: When analytical methods fail to
obtain the solution of a particular problem due to its complexity in
terms of constraints or number of variables, a numerical (or iterative)
method is used to find the solution. In this method, instead of solving
the problem directly, a general algorithm is applied for obtaining a
specific numerical solution.

10. METHODS FOR SOLVING OPERATIONS
RESEARCH MODELS
• Monte Carlo method : This method is based upon the idea of
experimenting on a mathematical model by inserting into the model
specific values of decision variables for a selected period of time
under different conditions and then observing the effect on the
criterion chosen. In this method, random samples of specified
random variables are drawn to know how the system is behaving

11. METHODOLOGY OF OPERATIONS RESEARCH

12. COMPUTER SOFTWARE FOR OPERATIONS
RESEARCH

13. Linear Programming:
Applications and Model Formulation

14. • General Structure of an LP Model

15. GUIDELINES ON LINEAR PROGRAMMING
MODEL FORMULATION
• Step 1: Identify the decision variables
Step 2: Identify the problem data
Step 3: Formulate the constraints
Step 4: Formulate the objective function

16. Example
• A manufacturing company is engaged in producing
three types of products: A, B and C. The production
department produces, each day, components
sufficient to make 50 units of A, 25 units of B and 30
units of C. The management is confronted with the
problem of optimizing the daily production of the
products in the assembly department, where only 100
man-hours are available daily for assembling the
products. The following additional information is
available:
• The company has a daily order commitment for 20
units of products A and a total of 15 units of products
B and C. Formulate this problem as an LP model so as
to maximize the total profit

17. Example 2 (Finance)
• XYZ is an investment company. To aid in its investment decision, the company has developed
the investment alternatives for a 10-year period, as given in the following table. The return
on investment
is expressed as an annual rate of return on the invested capital. The risk coefficient and
growth potential are subjective estimates made by the portfolio manager of the company.
The terms of investment is the average length of time period required to realize the return
on investment as indicated
• The objective of the company is to maximize the return on its investments. The guidelines
for selecting the portfolio are:
(i) The average length of the investment for the portfolio should not exceed 7 years.
(ii) The average risk for the portfolio should not exceed 5.
(iii) The average growth potential for the portfolio should be at least 10%.
(iv) At least 10% of all available funds must be retained in the form of cash, at all times.
Formulate this problem as an LP model to maximize total return

18. Example 3 (Marketing)
• An advertising company wishes to plan an advertising campaign for three
different media: television, radio and a magazine. The purpose of the
advertising is to reach as many potential customers as possible. The
following are the results of a market study:
• The company does not want to spend more than Rs 8,00,000 on
advertising. It is further required that
(i) at least 2 million exposures take place amongst women,
(ii) the cost of advertising on television be limited to Rs 5,00,000,
(iii) at least 3 advertising units be bought on prime day and two units
during prime time; and
(iv) the number of advertising units on the radio and the magazine should
each be between 5 and 10.
Formulate this problem as an LP model to maximize potential customer
reach.

19. Liner Programming: Graphical Method
• Use the graphical method to solve the following LP problem.
• Maximize Z = 15x1 + 10x2
subject to the constraints
(i) 4x1 + 6x2 ≤ 360,
(ii) 3x1 + 0x2 ≤ 180,
(iii) 0x1 + 5x2 ≤ 200
and x1, x2 ≥ 0

20. Example 2
• Use the graphical method to solve the following LP problem.
Maximize Z = 2x 1 + x2
subject to the constraints
(i) x1 + 2x2 ≤ 10, (ii) x1 + x2 ≤ 6,
(iii) x1 – x2 ≤ 2, (iv) x1 – 2x2 ≤ 1
and x 1, x2 ≥ 0

21. Example 3
• The ABC Company has been a producer of picture tubes for television sets and
certain printed circuits for radios. The company has just expanded into full scale
production and marketing of AM and AM-FM radios. It has built a new plant that
can operate 48 hours per week. Production of an AM radio in the new plant will
require 2 hours and production of an AM-FM radio will require 3 hours. Each AM
radio will contribute Rs 40 to profits while an AM-FM radio will contribute Rs 80
to profits. The marketing department, after extensive
research has determined that a maximum of 15AM radios and 10 AM-FM radios
can be sold each week
• Formulate a linear programming model to determine the optimum production
mix of AM and FM radios that will maximize profits
• Solve this problem using graphical method

22. Examples on Minimization LP Problem
• Use the graphical method to solve the following LP problem.
Minimize Z = 3x 1 + 2x2
subject to the constraints
(i) 5x1 + x2 ≥ 10, (ii) x1 + x2 ≥ 6, (iii) x1 + 4x2 ≥ 12
and x1, x2 ≥ 0.

23. Example 2 (min Z)
• Use the graphical method to solve the following LP problem.
Minimize Z = – x1 + 2x2
subject to the constraints
(i) – x1 + 3x2 ≤ 10, (ii) x1 + x2 ≤ 6, (iii) x1 – x2 ≤ 2
and x1, x2 ≥ 0

24. Mixed Constraints LP Problems
• Use the graphical method to solve the following LP problem.
Maximize Z = 7x1 + 3x2
subject to the constraints
(i) x1 + 2x2 ≥ 3 (ii) x1 + x2 ≤ 4 (iii) 0 ≤ x1 ≤ 5/2 (iv) 0 ≤ x2 ≤ 3/2
• and x1, x2 ≥ 0

25. Unbounded Solution
• Use the graphical method to solve the following LP problem:
Maximize Z = 3x1 + 4x2
• subject to the constraints
(i) x1 – x2 = –1 (ii) – x1 + x2 ≤ 0
• and x1, x2 ≥ 0.

26. Unbounded Solution Example 2
• Use graphical method to solve the following LP problem:
Maximize Z = 3x1 + 2x2
subject to the constraints
(i) x1 – x2 ≥ 1 (ii) x1 + x2 ≥ 3
and x1, x2 ≥ 0.

27. Infeasible Solution
• Use the graphical method to solve the following LP problem:
Maximize Z = 6x1 – 4x2
subject to the constraints
(i) 2x1 + 4x2 ≤ 4 (ii) 4x1 + 8x2 ≥ 16
and x1, x2 ≥ 0

28. Simplex Method
• STANDARD FORM OF AN LP PROBLEM
(i) All the constraints should be expressed as equations by adding
slack or surplus and/or artificial variables.
(ii) The right-hand side of each constraint should be made non-
negative (if not). This is done by multiplying both sides of the
resulting constraint by – 1.
(iii) The objective function should be of the maximization type

29. Simplex Method

30. Example 1
• Use the simplex method to solve the following LP problem.
• Maximize Z = 3x1 + 5x2 + 4x3
• subject to the constraints
• (i) 2x1 + 3x2 ≤ 8, (ii) 2x2 + 5x3 ≤ 10, (iii) 3x1 + 2x2 + 4x3 ≤ 15
• and x1, x2, x3 ≥ 0