Downloaded 17 times
Uploaded byTravis Klein
Oligopoly game theory
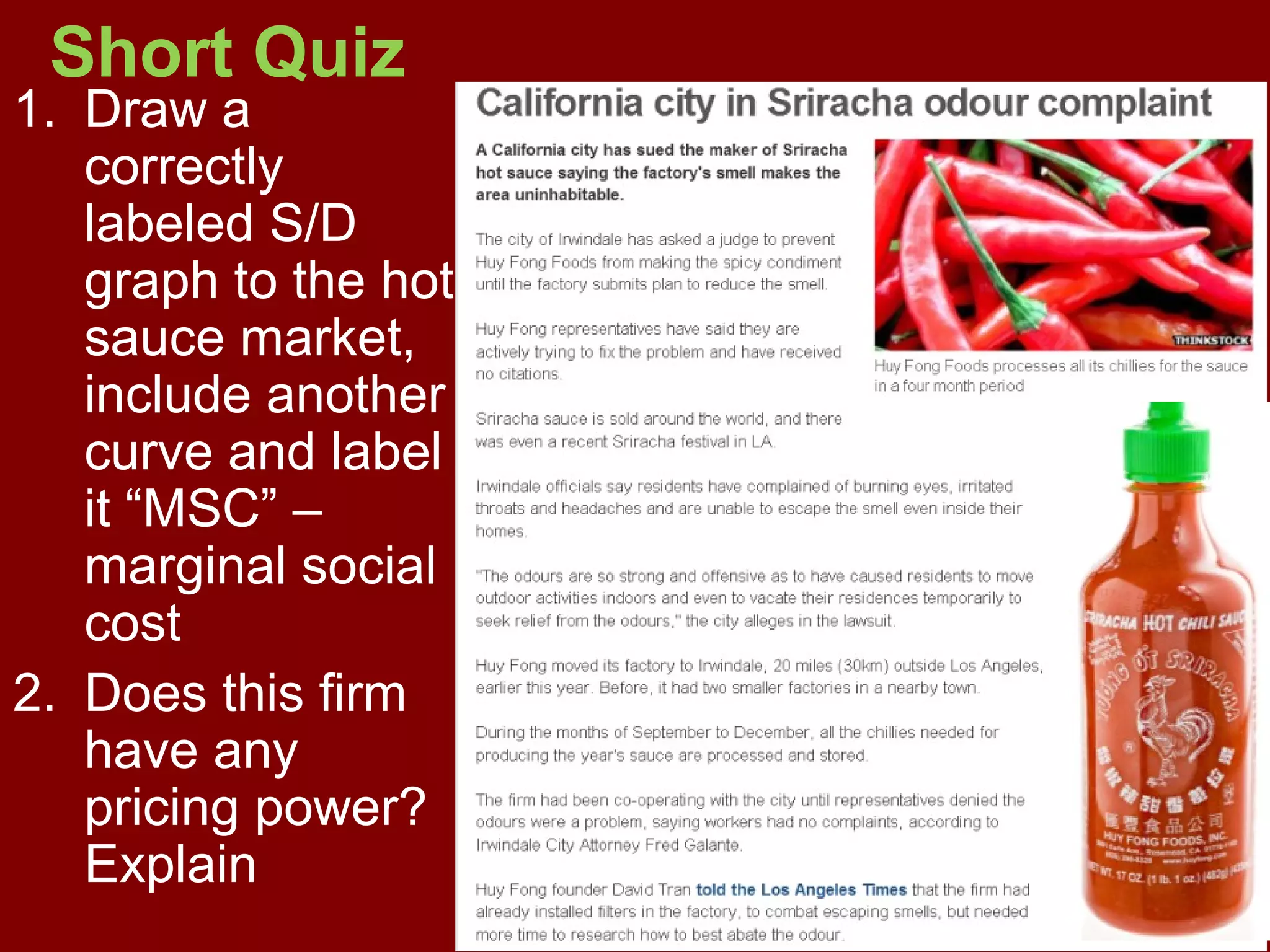
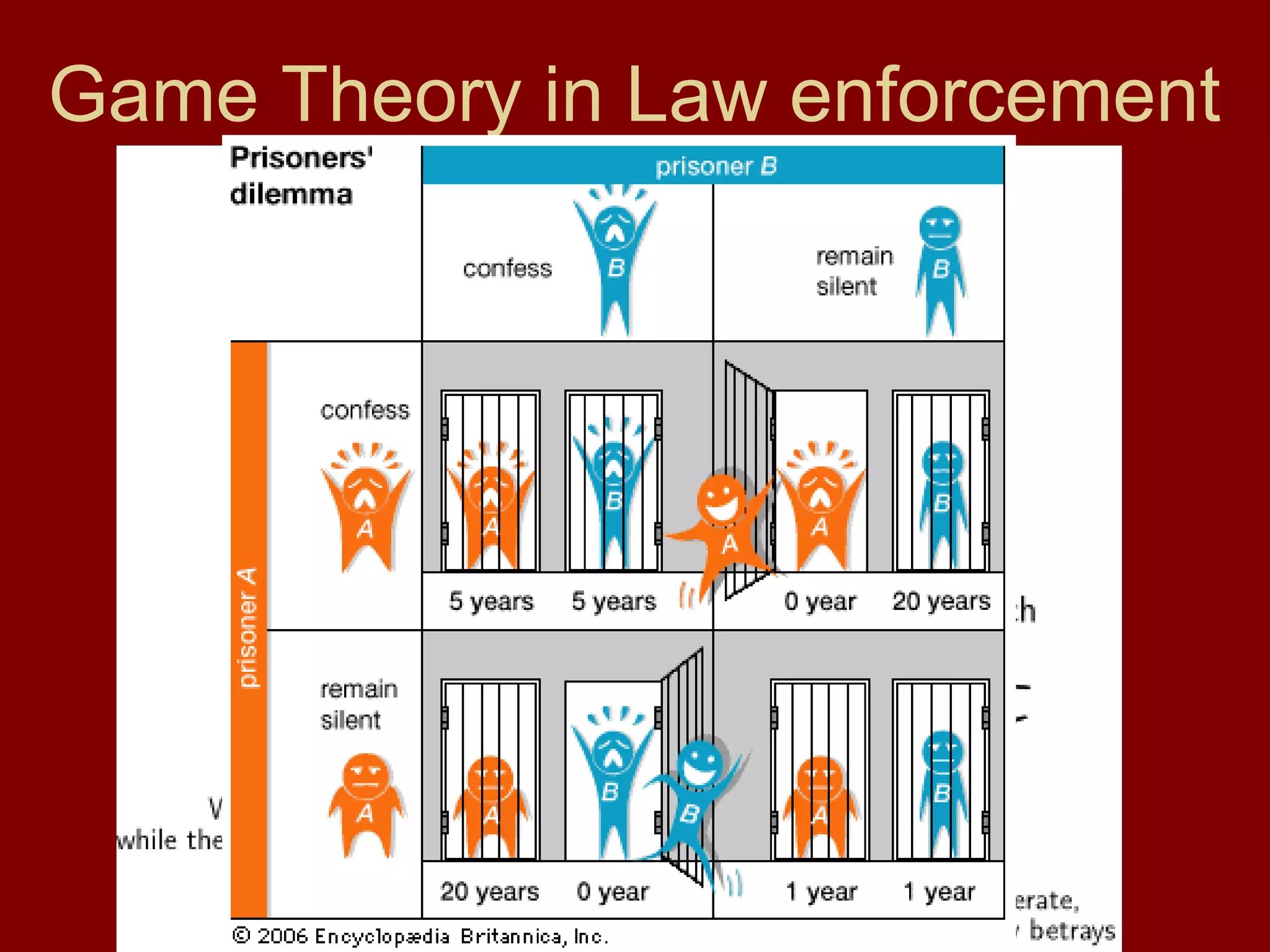
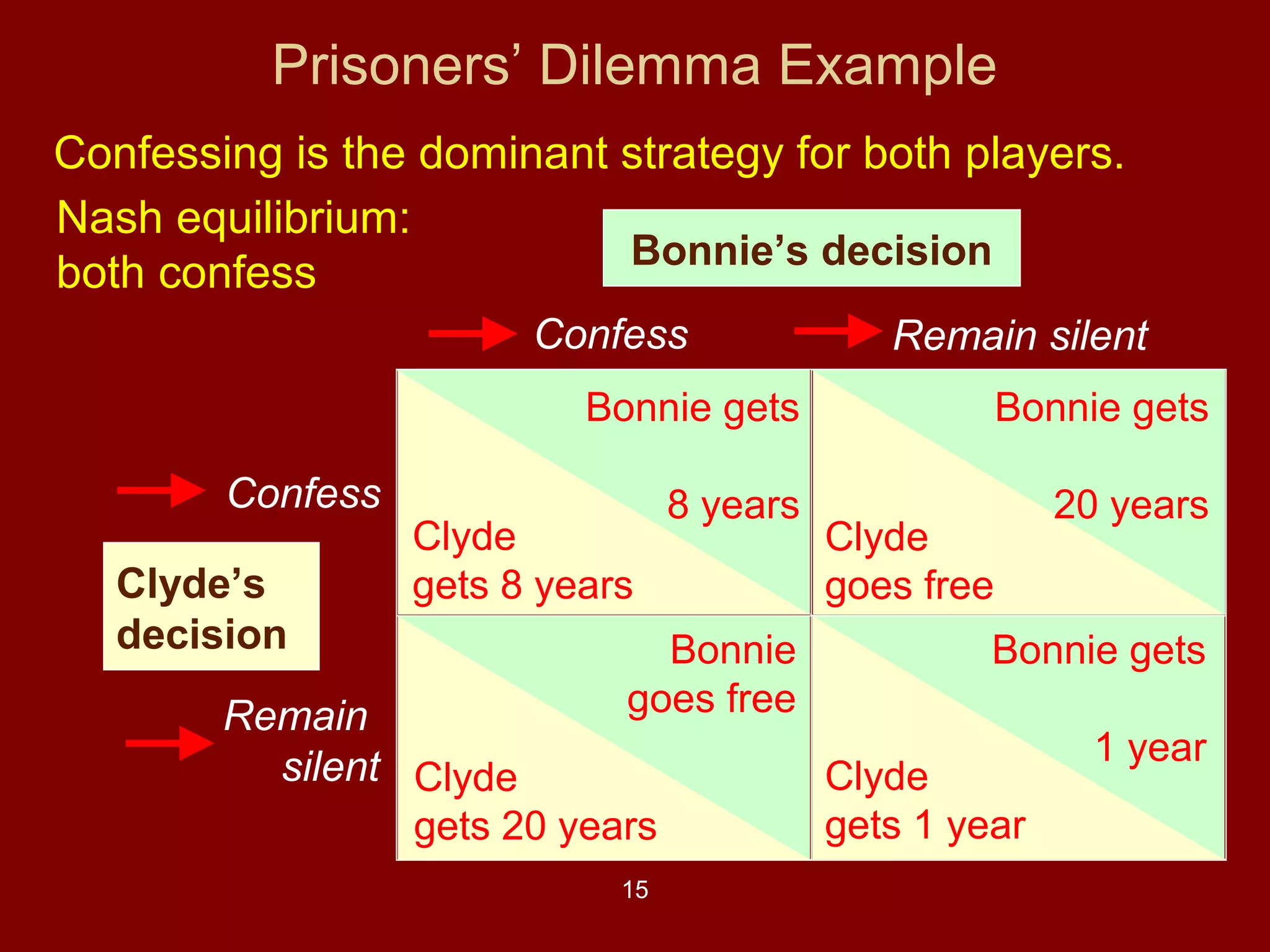
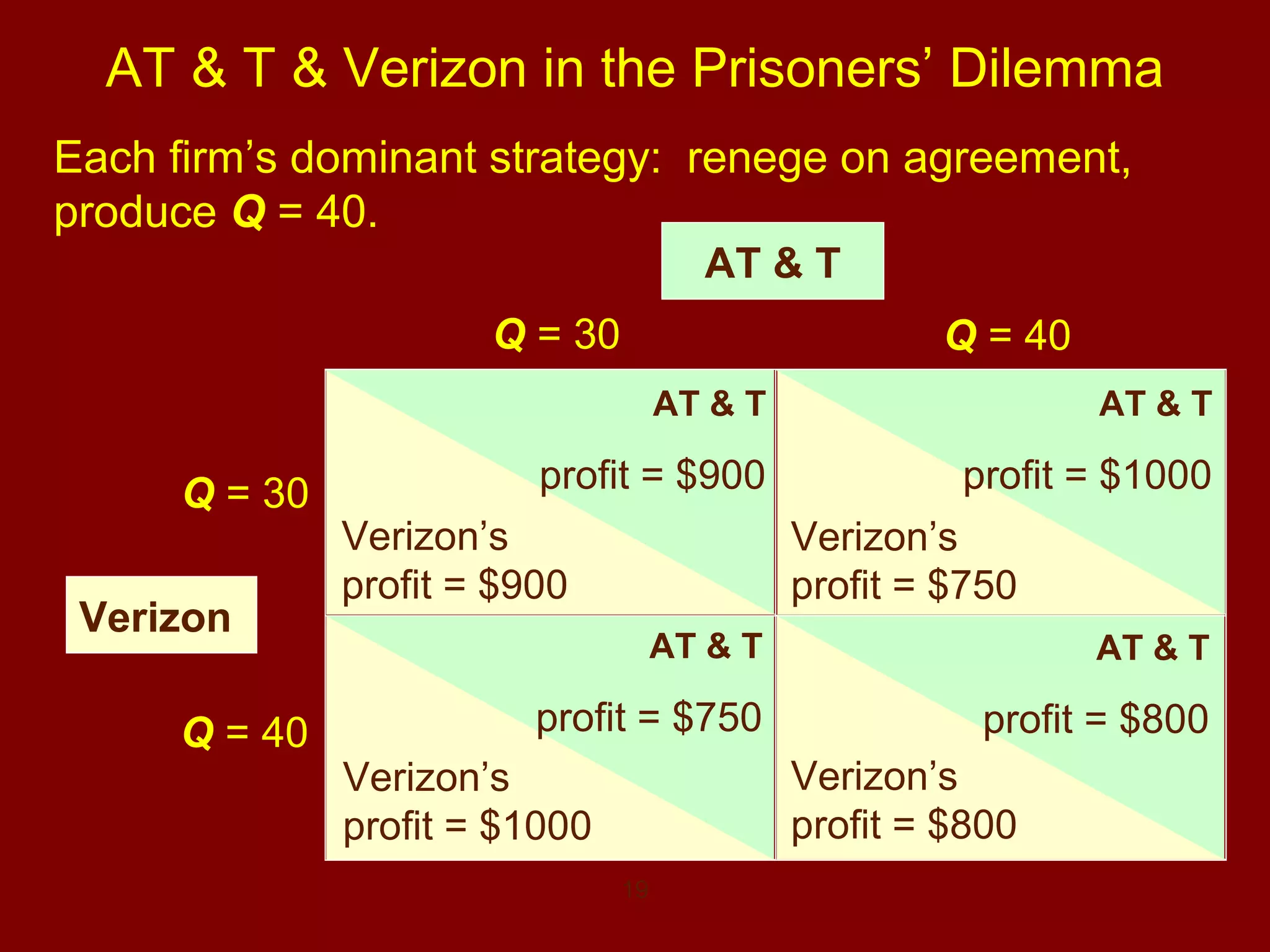
Here are payoff matrices for some of the game theory scenarios: Student helping partner: Partner studies Partner doesn't study Student helps Partner gets A, Student gets B Partner gets F, Student gets C Student doesn't help Partner gets C, Student gets D Partner gets F, Student gets D A's owner moving team: Oakland builds stadium Oakland doesn't build stadium Owner moves team Loss of fans and money, profit of $500m Profit of $1b Owner stays Loss of $200m, fans stay Loss of $500m Coke advertising: Coke advertises Coke doesn't advertise Pepsi advertises Profit of $1b each Profit of
More Related Content
Similar to Oligopoly game theory
Oligopoly game theory
- 1. Short Quiz 1. Drawa correctly labeled S/D graph to the hot sauce market, include another curve and label it “MSC” – marginal social cost 2. Does this firm have any pricing power? Explain
- 2. Verbal Bellringer • Doesyour marginal grade % bring up or down the average for the class? • Does your marginal attendance bring up or down the class attendence? Grade % Absences Tardies 60 0 1 76 0 1 74 1 1 60 1 10 38 1 4 80 1 2 81 2 4 70 2 10 89 2 6 87 3 0 60 4 22 56 5 10 97 6 0 61 10 7 47 16 8 Average % Ave AB Ave Tardies 69 3.60 5.73
- 3.
- 5. Ultimatum game • 2players, you don’t know the other • 20 pts (really $20, but I’m not that wealthy) • 1 person proposes a split, the other accepts or rejects, if rejected neither party gets points
- 7. Ultimatum Results • Inindustrialized cultures, people offer "fair" (i.e., 50:50) splits, and offers of less than 20% are often rejected • Why?
- 8.
- 9. Think back tothe ultimatum game yesterday • Think of another situation when you might have a similar problem to solve.
- 10. Economics? GAME THEORY “What willeveryone else do, if I do X ?” http://www.youtube.com/w atch?v=CemLiSI5ox8
- 11. Game Theory • Gametheory helps us understand oligopoly and other situations where “players” interact and behave strategically. • Dominant strategy: a strategy that is best for a player in a game regardless of the strategies chosen by the other players • Prisoners’ dilemma: a “game” between two captured criminals that illustrates why cooperation is difficult even when it is mutually beneficial
- 12. Prisoners’ Dilemma Example •The police have caught Bonnie and Clyde, two suspected bank robbers, but only have enough evidence to imprison each for 1 year. • The police question each in separate rooms, offer each the following deal: – If you confess and implicate your partner, you go free. – If you do not confess but your partner implicates you, you get 20 years in prison. – If you both confess, each gets 8 years in prison.
- 13. Game Theory inLaw enforcement
- 14.
- 15. Prisoners’ Dilemma Example Confessingis the dominant strategy for both players. Nash equilibrium: Bonnie’s decision both confess Confess Remain silent Bonnie gets Confess Clyde’s decision Bonnie gets 8 years 20 years Clyde gets 8 years Bonnie goes free Remain silent Clyde gets 20 years 15 Clyde goes free Bonnie gets Clyde gets 1 year 1 year
- 16. Prisoners’ Dilemma Example •Outcome: Bonnie and Clyde both confess, each gets 8 years in prison. • Both would have been better off if both remained silent. • But even if Bonnie and Clyde had agreed before being caught to remain silent, the logic of self-interest takes over and leads them to confess. 16
- 17. Vocabulary for gametheory Pay off matrix Nash Equilibrium
- 18. Oligopolies as aPrisoners’ Dilemma • When oligopolies form a cartel in hopes of reaching the monopoly outcome, they become players in a prisoners’ dilemma. • Our earlier example: – AT & T and Verizon are duopolists in Smalltown. – The cartel outcome maximizes profits: Each firm agrees to serve Q = 30 customers. • Here is the “payoff matrix” for this example… OLIGOPOLY 18
- 19. AT & T& Verizon in the Prisoners’ Dilemma Each firm’s dominant strategy: renege on agreement, produce Q = 40. AT & T Q = 30 Q = 40 AT & T Q = 30 Verizon Q = 40 AT & T profit = $900 profit = $1000 Verizon’s profit = $900 Verizon’s profit = $750 AT & T AT & T profit = $750 profit = $800 Verizon’s profit = $800 Verizon’s profit = $1000 19
- 20. Opening Bell On oneside of your white “board” write a large X and a large O on the other side like this X O
- 21. Let’s play agame for points If all X’s are played 3 Xs and 1 O played 2 X and 2 O’s played 1 X and 3 Os played All O’s played X everyone loses 1 point each x gets 1 point, O loses 1 point each X gets 2 points, O loses 1 point each x wins 3 points each O loses 1 point everyone wins 1 point O
- 22. Lack of Competition •Oligopolies sometimes figure out competition hurts their profits, so……….
- 23.
- 24. If firms discussand agreed on new prices… This is called collusion. And you formed a cartel. Collusion = setting of prices by rival firms Cartel = groups of rival firms that try to fix prices to increase profits **Drug cartels – don’t compete on price In the United States, it is illegal
- 25. Meanwhile…. • OPEC –Organization of Petroleum Exporting Countries (1960-present)
- 26. How does OPECindirectly set prices?6 months, OPEC representatives Every and economists meet in Vienna to decide production. $/Barrel S after meeting 100 S Most Economists think cartels don’t work in the long term, why? 75 50 D 8 bi 10 billion Q/barrels
- 27. Dominant Strategy? forthis scenario
- 28. ACTIVE LEARNING 3 The “farewars” game The players: American Airlines and United Airlines The choice: cut fares by 50% or leave fares alone – If both airlines cut fares, each airline’s profit = $400 million – If neither airline cuts fares, each airline’s profit = $600 million – If only one airline cuts its fares, its profit = $800 million the other airline’s profits = $200 million Draw the payoff matrix, find the Nash equilibrium. 28
- 29. ACTIVE LEARNING Answers Nash equilibrium: bothfirms cut fares 3 American Airlines Cut fares $400 million Don’t cut fares $200 million Cut fares United Airlines $400 million $800 million $800 million $600 million Don’t cut fares $200 million $600 million 29
- 30. Prisoners’ Dilemma andSociety’s Welfare • The non cooperative oligopoly equilibrium – Bad for oligopoly firms: prevents them from achieving monopoly profits – Good for society: Q is closer to the socially efficient output P is closer to MC • In other prisoners’ dilemmas, the inability to cooperate may reduce social welfare. – e.g., arms race, overuse of common resources OLIGOPOLY
- 31. Another Example: NegativeCampaign Ads • Election with two candidates, “R” and “D.” • If R runs a negative ad attacking D, 3000 fewer people will vote for D: 1000 of these people vote for R, the rest abstain. • If D runs a negative ad attacking R, R loses 3000 votes, D gains 1000, 2000 abstain. • R and D agree to refrain from running attack ads. Will each one stick to the agreement? 31
- 32. Another Example: NegativeCampaign Ads Each candidate’s dominant strategy: run attack ads. R’s decision Do not run attack ads (cooperate) Do not run attack ads (cooperate) D’s decision Run attack ads (defect) no votes lost or gained no votes lost or gained Run attack ads (defect) R gains 1000 votes D loses 3000 votes R loses 3000 votes D gains 1000 votes R loses 2000 votes D loses 2000 votes
- 33. Another Example: NegativeCampaign Ads • Nash eq’m: both candidates run attack ads. • Effects on election outcome: NONE. Each side’s ads cancel out the effects of the other side’s ads. • Effects on society: NEGATIVE. Lower voter turnout, higher apathy about politics, less voter scrutiny of elected officials’ actions.
- 35. Mankiw Chapter 17Assignment • Problems #4 , 5, 6, 9 • QE #1 • John Nash Greg Mankiw
- 36. Table 17-17. Considera small town that has two grocery stores from which residents can choose to buy a gallon of milk. The store owners each must make a decision to set a high milk price or a low milk price. The payoff table, showing profit per week, is provided here. The profit in each cell is shown as (Store 1, Store 2). 1. Refer to Table 17-17. If grocery store 1 sets a high price, what price should grocery store 2 set? And what will grocery store 2's payoff equal? a. Low price, $800 b. High price, $100 c. Low price, $500 d. High price, $650 e. Low price, $650 3. What is the Nash Equilibrium in this pricing problem? 2. Refer to Table 17-17. What is grocery store 1's dominant strategy? a. Grocery store 1 does not have a dominant strategy. b. Grocery store 1 should always set a low price. c. Grocery store 1 should always set a high price. d. Grocery store 1 should set a low price when grocery store 2 sets a low price, and grocery store 1 should set a high price when grocery store 2 sets a high price. e. Grocery store 1 should set a low price when grocery store 2 sets a high price, and grocery store 1 should set a high price when grocery store 2 sets a low price.
- 37. Game Theory problems •Write a pay off matrix for the following scenarios: • A student deciding to help their partner do school work or not • The Oakland Athletics owner deciding whether or not to move the team if Oakland doesn’t build a new stadium • Coke deciding whether or not to advertise • A student deciding whether or not to study for an exam • A quarterback deciding whether or not to pass or run the ball • Verizon trying to decide whether or not to cut its fees vs AT&T • BK deciding whether or not to advertise on 12th Avenue • American Airlines deciding whether or not to upgrade its planes
Editor's Notes
- #12 “Players” can be people, firms, countries, or other entities. A “game” is a situation in which players interact. A “strategy” is a decision or decision-plan chosen by a player, which takes into account the behavior and likely reactions of other players.
- #13 SUGGESTION: Instead of showing this slide, ask for two volunteers to be your prisoners. You should pick two students that sit in different parts of the classroom, who are less likely to know each other. Tell them they will be playing bank robbers who have been caught. You are going to interrogate each one separately, like they do on police dramas (have any 20-year-olds heard of NYPD Blue?). Ask Student #2 to step out of the room for a few moments. Offer to Student #1 the deal described on this slide. Make a note of his or her choice, but do not write it on the board. Have Student #2 step into the room, and ask Student #1 to wait outside. Offer to Student #2 the deal described on this slide. Ask the class not to give any hints about the decision that Student #1 made. Make a note of Student #2’s choice. Invite Student #1 back into the room. Write down both of their choices on the board and reveal to each of them their fate. Hopefully, each student plays the “confess” strategy, so that the outcome of this role-play is the classic Prisoner’s Dilemma Nash Equilibrium. But even if the outcome is different, that’s okay. Ask each student to give the reasons for the strategy he or she chose. Explain why you would have expected both to play the “confess” strategy, and show the payoff matrix on the next slide. I’m telling you, students LOVE this. It takes a little longer to get through the material, but the material has much more impact then merely lecturing on the Bonnie and Clyde example.
- #16 This slide is animated carefully as follows: 1) If Clyde confesses, then Bonnie gets 8 years if she confesses or 20 years if she does not. 2) If Clyde remains silent, Bonnie goes free if she confesses or gets 1 year if she does not. At this point, it may be worth mentioning that Bonnie’s best move is to confess, regardless of Clyde’s decision – hence, “confess” is Bonnie’s dominant strategy. 3) If Bonnie confesses, Clyde gets 8 years if he confesses or 20 years if he does not. 4) If Bonnie remains silent, Clyde goes free if he confesses or gets 1 year if he does not. Regardless of Bonnie’s decision, Clyde’s best move is to confess. Both players have a dominant strategy of confessing.
- #17 The prisoners’ dilemma illustrates why cooperation is so difficult even when it is in both players’ mutual interest.
- #19 The term “payoff matrix” is fairly standard in microeconomics, so it may be worth mentioning to your students. However, the textbook does not use this term, so you may wish to delete it from this presentation. If so, please note that the term appears in two different places in this presentation – once on this slide, and once on the bottom of the slide containing the instructions for Active Learning 3.
- #29 The title I have given this game (the “fare wars” game) might be too much of a hint about what happens in the Nash equilibrium. Feel free to change it to something like “airfare pricing strategies.”
- #31 In the arms race “game,” each of the superpowers would be better off if they could cooperate and sign an agreement to disarm. But the logic of self-interest dictates that each country will arm itself to the teeth. As a result, both countries are worse off for two reasons: 1) The risk of nuclear annihilation is higher. 2) Resources consumed in the arms race could have been used elsewhere. The following slide presents another example in which the inability to cooperate reduces social welfare.
- #32 This slide and the two that follow work through an example that is especially topical during election years. It does not appear in the textbook, so it is not supported with Test Bank questions or Study Guide questions. Please feel free to omit it from your presentation. Yet, I encourage you to consider keeping this example. Students find it interesting: it explains why negative ads flood the airwaves prior to elections, and it explains the effects of these ads on society.
- #33 Understanding the payoffs: Mutual cooperation is the benchmark outcome: Payoffs in other cells are differences in votes received relative to the mutual cooperation outcome. (This does not mean that there is a tie in the mutual cooperation outcome or the mutual defection outcome. It means that the winner will be decided by factors other than whether attack ads run or not.) Consider R’s decision. R is better off defecting (running ads attacking D) whether D cooperates or defects. If D cooperates, R’s attack ads result in 1000 more votes for R and 3000 fewer votes for D. If D defects, R loses fewer votes if he runs the attack ad than if he cooperates. Hence, running attack ads is a dominant strategy for R. The payoffs here are symmetric, so defecting is also D’s dominant strategy. This game has a Nash equilibrium in which both candidates defect. This is why, in the real world, we see so many attack ads in the weeks leading up to an election.
- #34 This slide considers the effects of the attack ads on election outcomes and on social well-being. The negative impact on social well-being is like a negative externality: the “bystanders” are voters who are worse off as a result of the candidates’ actions.