Download to read offline
Uploaded bySherif Abdelfattah
Oblivious Neural Network Predictions via MiniONN Transformations
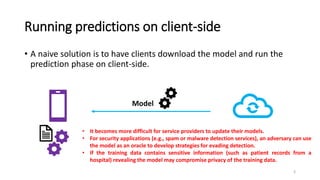
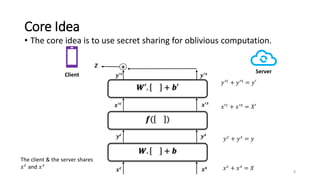
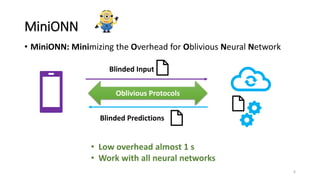
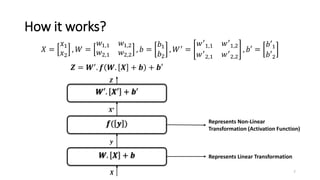
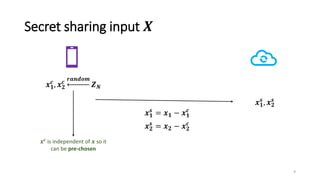
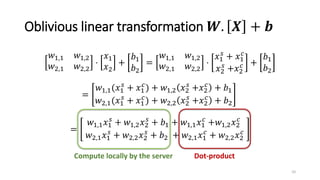
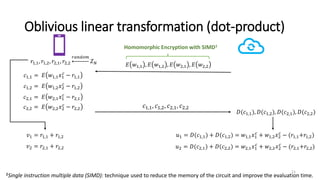
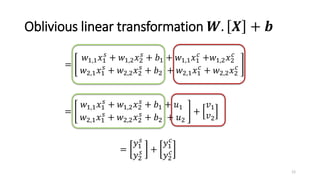
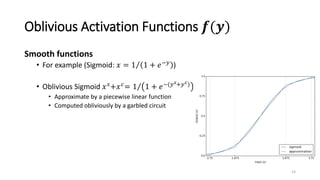
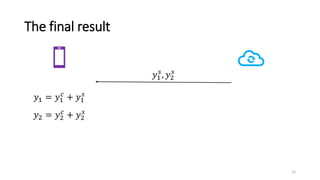
This document summarizes the Oblivious Neural Network Predictions via MiniONN Transformations paper. 1) MiniONN is a technique that allows a server to perform predictions using a neural network model on a client's private input, while revealing no information about the input or model. It uses secret sharing and oblivious computation to perform predictions without privacy violations. 2) MiniONN works by having the client and server secretly share the client's input between them. Oblivious linear transformations and activation functions are then computed to produce the prediction, without either party learning the other's data. 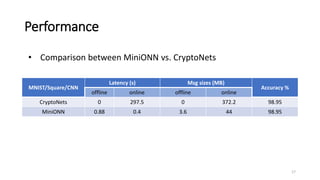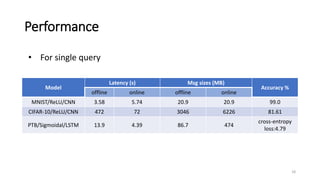3) Experiments show MiniONN can perform predictions on common models like CNNs and LSTMs with low
More Related Content
Similar to Oblivious Neural Network Predictions via MiniONN Transformations
Oblivious Neural Network Predictions via MiniONN Transformations
- 1. Oblivious Neural Network Predictionsvia MiniONN Transformations Presented by: Sherif Abdelfattah Liu, J., Juuti, M., Lu, Y., & Asokan, N. (2017, October). Oblivious neural network predictions via minionn transformations. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (pp. 619-631). ACM. (121 citation) 1
- 2. Machine Learning asa Service Input Predictions This way is a violation of clients’ privacy 2
- 3. Running predictions onclient-side • A naive solution is to have clients download the model and run the prediction phase on client-side. Model • It becomes more difficult for service providers to update their models. • For security applications (e.g., spam or malware detection services), an adversary can use the model as an oracle to develop strategies for evading detection. • If the training data contains sensitive information (such as patient records from a hospital) revealing the model may compromise privacy of the training data. 3
- 4. Oblivious Neural Networks(ONN) The solution is using make the neural network oblivious • The server learns nothing about the client’s input. • The clients learn nothing about the model. 4
- 5. MiniONN Blinded Input Blinded Predictions ObliviousProtocols • Low overhead almost 1 s • Work with all neural networks • MiniONN: Minimizing the Overhead for Oblivious Neural Network 6
- 6. How it works? 𝑋= 𝑥1 𝑥2 , 𝑊 = 𝑤1,1 𝑤1,2 𝑤2,1 𝑤2,2 , 𝑏 = 𝑏1 𝑏2 , 𝑊′ = 𝑤′ 1,1 𝑤′ 1,2 𝑤′ 2,1 𝑤′ 2,2 , 𝑏′ = 𝑏′1 𝑏′2 𝑾′. 𝑿′ + 𝒃′ 𝒇( 𝒚 ) 𝑾. 𝑿 + 𝒃 𝑿 𝒚 𝑿’ 𝒁 Represents Linear Transformation Represents Non-Linear Transformation (Activation Function) 𝒁 = 𝑾′. 𝒇 𝑾. 𝑿 + 𝒃 + 𝒃′ 7
- 7. Core Idea • Thecore idea is to use secret sharing for oblivious computation. 𝑾′. + 𝒃′ 𝒇( ) 𝑾. + 𝒃 𝒚𝒄 𝒙′𝒄 𝒙𝐜 𝒙𝐬 𝒚𝒔 𝒙′𝒔 Client Server 𝒚′𝒄 𝒚′𝒔 𝒁 𝑥𝑐 + 𝑥𝑠 = 𝑋 𝑦𝑐 + 𝑦𝑠 = 𝑦 𝑥′𝑐 + 𝑥′𝑠 = 𝑋′ 𝑦′𝑐 + 𝑦′𝑠 = 𝑦′ The client & the server shares 𝑥𝑐 and 𝑥𝑠 8
- 8. Secret sharing input𝑿 𝒙𝟏 𝒄 , 𝒙𝟐 𝒄 𝒓𝒂𝒏𝒅𝒐𝒎 𝒁𝑵 𝒙𝟏 𝒔 = 𝒙𝟏 − 𝒙𝟏 𝒄 𝒙𝟐 𝒔 = 𝒙𝟐 − 𝒙𝟐 𝒄 𝒙𝟏 𝒔 , 𝒙𝟐 𝒔 𝒙𝒄 is independent of 𝒙 so it can be pre-chosen 9
- 9. Oblivious linear transformation𝑾. 𝑿 + 𝒃 𝑤1,1 𝑤1,2 𝑤2,1 𝑤2,2 ⋅ 𝑥1 𝑥2 + 𝑏1 𝑏2 = 𝑤1,1 𝑤1,2 𝑤2,1 𝑤2,2 ⋅ 𝑥1 𝑠 + 𝑥1 𝑐 𝑥2 𝑠 +𝑥2 𝑐 + 𝑏1 𝑏2 = 𝑤1,1(𝑥1 𝑠 + 𝑥1 𝑐 ) + 𝑤1,2 𝑥2 𝑠 +𝑥2 𝑐 + 𝑏1 𝑤2,1(𝑥1 𝑠 + 𝑥1 𝑐 ) + 𝑤2,2 𝑥2 𝑠 +𝑥2 𝑐 + 𝑏2 = 𝑤1,1𝑥1 𝑠 + 𝑤1,2𝑥2 𝑠 + 𝑏1 + 𝑤1,1𝑥1 𝑐 +𝑤1,2𝑥2 𝑐 𝑤2,1𝑥1 𝑠 + 𝑤2,2𝑥2 𝑠 + 𝑏2 + 𝑤2,1𝑥1 𝑐 + 𝑤2,2𝑥2 𝑐 Compute locally by the server Dot-product 10
- 10. Oblivious linear transformation(dot-product) 𝑟1,1, 𝑟1,2, 𝑟2,1, 𝑟2,2 𝑟𝑎𝑛𝑑𝑜𝑚 𝑍𝑁 𝐸 𝑤1,1 , 𝐸 𝑤1,2 , 𝐸 𝑤2,1 , 𝐸 𝑤2,2 Homomorphic Encryption with SIMD1 1Single instruction multiple data (SIMD): technique used to reduce the memory of the circuit and improve the evaluation time. 𝑐1,1 = 𝐸 𝑤1,1𝑥1 𝑐 − 𝑟1,1 𝑐1,2 = 𝐸 𝑤1,2𝑥2 𝑐 − 𝑟1,2 𝑐2,1 = 𝐸 𝑤2,1𝑥1 𝑐 − 𝑟2,1 𝑐2,2 = 𝐸 𝑤2,2𝑥2 𝑐 − 𝑟2,2 𝑐1,1, 𝑐1,2, 𝑐2,1, 𝑐2,2 𝐷(𝑐1,1), 𝐷(𝑐1,2), 𝐷(𝑐2,1), 𝐷(𝑐2,2) 𝑢1 = 𝐷(𝑐1,1) + 𝐷(𝑐1,2) = 𝑤1,1𝑥1 𝑐 + 𝑤1,2𝑥2 𝑐 − (𝑟1,1+𝑟1,2) 𝑢2 = 𝐷(𝑐2,1) + 𝐷(𝑐2,2) = 𝑤2,1𝑥1 𝑐 + 𝑤2,2𝑥2 𝑐 − (𝑟2,1+𝑟2,2) 𝑣1 = 𝑟1,1 + 𝑟1,2 𝑣2 = 𝑟2,1 + 𝑟2,2 11
- 11. Oblivious linear transformation𝑾. 𝑿 + 𝒃 = 𝑤1,1𝑥1 𝑠 + 𝑤1,2𝑥2 𝑠 + 𝑏1 + 𝑤1,1𝑥1 𝑐 +𝑤1,2𝑥2 𝑐 𝑤2,1𝑥1 𝑠 + 𝑤2,2𝑥2 𝑠 + 𝑏2 + 𝑤2,1𝑥1 𝑐 + 𝑤2,2𝑥2 𝑐 = 𝑤1,1𝑥1 𝑠 + 𝑤1,2𝑥2 𝑠 + 𝑏1 + 𝑢1 𝑤2,1𝑥1 𝑠 + 𝑤2,2𝑥2 𝑠 + 𝑏2 + 𝑢2 + 𝑣1 𝑣2 = 𝑦1 𝑠 𝑦2 𝑠 + 𝑦1 𝑐 𝑦2 𝑐 12
- 12. Oblivious Activation Functions𝒇(𝒚) Piecewise linear functions • For example (ReLU: 𝑥 = compare(𝑦, 0)) • Oblivious ReLU 𝑥𝑠+𝑥𝑐= compare 𝑦𝑠 + 𝑦𝑐, 0 • Computed obliviously by a garbled circuit2 2garbled circuit: is a two-party computation (2PC) technique that allow two parties to jointly compute a function without learning each other’s input. 13
- 13. Oblivious Activation Functions𝒇(𝒚) Smooth functions • For example (Sigmoid: 𝑥 = Τ 1 1 + 𝑒−𝑦 ) • Oblivious Sigmoid 𝑥𝑠+𝑥𝑐= Τ 1 1 + 𝑒−(𝑦𝑠+𝑦𝑐) • Approximate by a piecewise linear function • Computed obliviously by a garbled circuit 14
- 14. The final result 𝑦1 𝑠 ,𝑦2 𝑠 𝑦1 = 𝑦1 𝑐 + 𝑦1 𝑠 𝑦2 = 𝑦2 𝑐 + 𝑦2 𝑠 15
- 15. Performance 1. MNIST (60000 training images and 10 000 test images) • Handwriting recognition • CNN model • ReLU activation function 2. CIFAR-10 (50 000 training images and 10 000 test images) • Image classification • CNN model • ReLU activation function 3. Penn Treebank (PTB) (929 000 training words, 73 000 validation words, and 82 000 test words.) • language modeling: predicting next words given the previous words • Long Short Term Memory (LSTM): commonly used for language modeling • Sigmoidal activation function 16
- 16. Performance MNIST/Square/CNN Latency (s) Msgsizes (MB) Accuracy % offline online offline online CryptoNets 0 297.5 0 372.2 98.95 MiniONN 0.88 0.4 3.6 44 98.95 • Comparison between MiniONN vs. CryptoNets 17
- 17. Performance Model Latency (s) Msgsizes (MB) Accuracy % offline online offline online MNIST/ReLU/CNN 3.58 5.74 20.9 20.9 99.0 CIFAR-10/ReLU/CNN 472 72 3046 6226 81.61 PTB/Sigmoidal/LSTM 13.9 4.39 86.7 474 cross-entropy loss:4.79 • For single query 18
- 18.