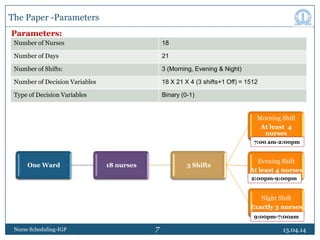
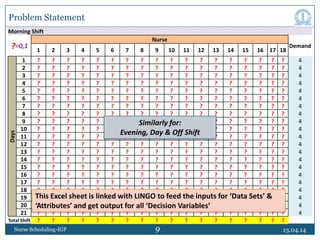
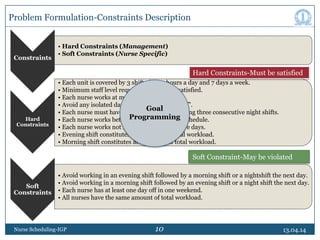
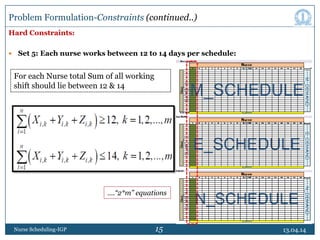
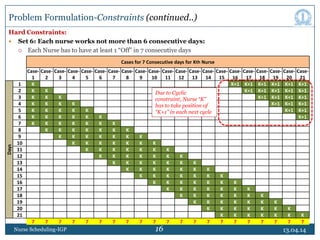
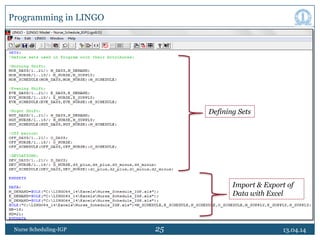
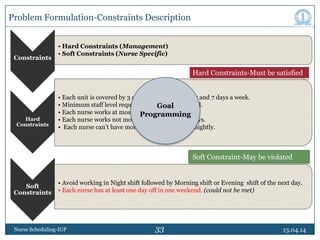
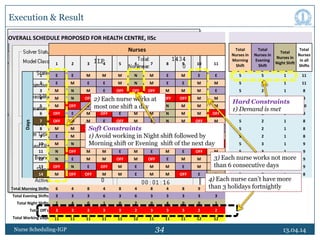
This document discusses nurse scheduling using integer goal programming. It begins with an introduction to nurse scheduling and the motivation for applying operations research techniques. It then reviews relevant literature on nurse scheduling models. The paper formulates the nurse scheduling problem with constraints to meet management objectives and nurse preferences. Notations and decision variables are defined for a scheduling model with 18 nurses, 21 days, and 3 shifts per day. The constraints include minimum staffing levels, assigning only one shift per nurse daily, and ensuring fair rotation of shifts. The goal is to generate cyclic schedules that satisfy constraints and optimize objectives like workload balance and nurse preferences.

1. I N T E R G E R G O A L P R O G R A M M I N G
13.04.14Nurse Scheduling-IGP
NURSE SCHEDULING
Prepared by-
Sowmiyan Morri
Swapnil Soni
DoMS, IISc
Course-
Applied Operations Research
Instructor-
Prof M Mathirajan
1

2. 2
Index
 Introduction to Nurse Scheduling
 Scheduling problem
 Motivation to adopt OR technique
 Research and Literature work
 Literature Review
 The Paper
 The Paper
 Parameters
 Problem Statement
 Problem Formulation
 Notations & Decision Variables
 Constraints
 Objective Function
13.04.14Nurse Scheduling-IGP
 Programming in LINGO (Optimization tool)
 Result
 Conclusion
 Achievements
 The way forward
 Applications
 Pilot Study at Health Centre, IISc
 Parameters
 Constraints
 Result
 References

3. 3
Introduction to Nurse Scheduling
13.04.14Nurse Scheduling-IGP
Motivation for applying Operations Research for Nurse Scheduling
Cyclical Nurse Schedule
Constraints
Hospitals requirement
Nurses’ preferences
Conventional Register
Question on:
•Tedious
•Time
•Accuracy
•Fairness
Mathematical Modeling
Advantages on:
•Tedious
•Time
•Accuracy
•Fairness
Prescriptive Model
Cause Response
Variables of 1st order Linear
Variables with Binary values Integer
Constraints with priorities Goal
Liner Integer Goal Programming
Operations Research

4. 4
Literature Review
13.04.14Nurse Scheduling-IGP
Authors Reference Literature Limitations
Arthur &
Ravindran
Arthur, J. L., & Ravindran,
A., A Multiple Objective Nurse
Scheduling
Model, IIE Transactions,
13(1), pp. 55-60, 1981
Research on modelling Nurse
Scheduling using goal
programming has been studied
which focused on two phases:
•Phase 1 is to assign the working
days and days off for each nurse
while
•Phase 2 is to assign the shift
types of their working days
•Small set of
constraints
•Limited problem
dimensions with the
size of nurses is 4
Musa &
Saxena
Musa, A. A., & Saxena, U.,
Scheduling Nurses Using
Goal-Programming
Techniques, IIE Transactions,
16(3), pp. 216 – 221, 1984
Used a 0-1 goal programming that
applied to one unit of a hospital
with the considerations of the
hospital policies and nurses’
preferences
•2 week planning
period
•1 one single shift
Ozkarahan
& Bailey
Ozkarahan, I. & Bailey, J.E.,
Goal Programming Model
Subsystem of A
Flexible Nurse Scheduling
Support System, IIE
Transactions, 20(3), pp.
306-316, 1988.
Nurse scheduling modelling
showed the
flexibility of goal programming in
handling various goals which
fulfilled the hospital’s objectives
and the nurses’ preferences.
•Small set of
constraints

5. 5 13.04.14Nurse Scheduling-IGP
Authors Reference Literature Limitations
Azaiez &
Al Sharif
Berrada, I., Ferland, J. A., &
Michelon, P., A Multi-objective
Approach to
Nurse Scheduling with Both Hard
and Soft Constraints, Socio-
Economic
Planning Sciences, 30(3), pp. 183-
193, 1996
Used the 0-1 goal programming
approach with the considerations
of hospital’s objectives as hard
constraints and the nurses’
preferences as soft constraints to
develop the schedules
•No cyclic
scheduling
Harvey
and
Kiragu
Harvey, H.M., & Kiragu, M., Cyclic
and Non-cyclic Scheduling of 12 h
Shift Nurses by Network
Programming, European Journal of
Operational
Research, 104, pp. 582-592, 1998
Presented a mathematical model
for cyclic and non-cyclic
scheduling of 12
hours shift nurses. The model is
quite flexible and can
accommodate a variety
of constraints
• With small
requirements
which are not
appropriate to
embed in real
situations
Chan and
Weil
Chan, P. & Weil, G., Cyclical Staff
Scheduling Using Constraint Logic
Programming, Lecture Notes on
Computer Sciences 2079, pp. 159-
175,
2001
Use of work cycles with various
constraints to produce
timetables of up to 150 people
•Small set of
constraints
Literature Review

6. 6
The Paper
13.04.14Nurse Scheduling-IGP
Author From
Ruzzakiah Jenal
School of Information Technology, Faculty of Science and Information
Technology,
Universiti Kebangsaan Malaysia, Selangor, Malaysia
Wan Rosmanira Ismail
School of Mathematical Sciences, Faculty of Science and Technology,
Universiti Kebangsaan Malaysia, Selangor, Malaysia
Liong Choong Yeun
Ahmed Oughalime
Published By LPPM ITB, ISSN: 1978-3043
Accepted for Publication April 13th, 2011

7. 7
The Paper -Parameters
13.04.14Nurse Scheduling-IGP
Number of Nurses 18
Number of Days 21
Number of Shifts: 3 (Morning, Evening & Night)
Number of Decision Variables 18 X 21 X 4 (3 shifts+1 Off) = 1512
Type of Decision Variables Binary (0-1)
Parameters:
One Ward 18 nurses 3 Shifts
Morning Shift
At least 4
nurses
Evening Shift
At least 4 nurses
Night Shift
Exactly 3 nurses
7:00 am-2:00pm
2:00pm-9:00pm
9:00pm-7:00am

8. 8 13.04.14Nurse Scheduling-IGP
Problem Statement
Objective:
Cyclic Nurse Scheduling:
To allot shifts to each Nurse for each day thereby generating a schedule of working days
and days off for each nurse in a ward of a hospital.
Physical Constraints:
(A) Hard Constraint
Meeting management objectives
(B) Soft constraints
Satisfaction of employees(Nurses), work/life balance
Logical Constraints:
(C) Cyclic Scheduling
A cyclic schedule consists of a set of work patterns which is rotated among a group of workers over a set of
scheduling horizon. At the end of the scheduling horizon each worker would have completed each pattern
exactly once.
Advantages:
• Fairness among nurses
•Considers nurses preferences
•Lead to maximizing satisfaction
•Help Nurses to provide Quality of services
“The right employees at the right time
and at the right cost while achieving a
high level of employee job satisfaction”

9. 9
Problem Statement
13.04.14Nurse Scheduling-IGP
Morning Shift
?=0,1
Nurse
Demand
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Days
1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
2 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
3 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
4 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
5 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
6 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
7 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
8 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
9 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
10 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
11 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
12 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
13 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
14 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
15 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
16 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
17 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
18 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
19 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
20 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
21 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4
Total Shift ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Similarly for:
Evening, Day & Off Shift
This Excel sheet is linked with LINGO to feed the inputs for ‘Data Sets’ &
‘Attributes’ and get output for all ‘Decision Variables’

10. 10 13.04.14Nurse Scheduling-IGP
Constraints
• Hard Constraints (Management)
• Soft Constraints (Nurse Specific)
Hard
Constraints
• Each unit is covered by 3 shifts for 24 hours a day and 7 days a week.
• Minimum staff level requirement must be satisfied.
• Each nurse works at most one shift a day.
• Avoid any isolated days patterns of “off-on-off”.
• Each nurse must have three days off after having three consecutive night shifts.
• Each nurse works between 12 to 14 days per schedule.
• Each nurse works not more than 6 consecutive days.
• Evening shift constitutes at least 25% of total workload.
• Morning shift constitutes at least 30% of total workload.
Soft
Constraints
• Avoid working in an evening shift followed by a morning shift or a nightshift the next day.
• Avoid working in a morning shift followed by an evening shift or a night shift the next day.
• Each nurse has at least one day off in one weekend.
• All nurses have the same amount of total workload.
Problem Formulation-Constraints Description
Hard Constraints-Must be satisfied
Soft Constraint-May be violated
Goal
Programming

11. 11
Notations
The following notations are used to specify the model:
 n = number of days in the schedule (n = 21)
 m = number of nurses available for the unit of interest (m = 18)
 i = index for days, i = 1…n
 k = index for nurses, k = 1…m
 Pi = staff requirement for morning shift of day i, i = 1…n
 Ti = staff requirement for evening shift of day i, i = 1…n
 Mi = staff requirement for night shift of day i, i = 1…n
13.04.14Nurse Scheduling-IGP
Problem Formulation- Notation & Decision Variables
Decision Variables

12. 12
Hard Constraints:
 Set 1: Minimum staff level requirement must be satisfied:
 For Morning shift (Where Pi=4)
 For Evening shift (Where Ti=4)
 For Night shift (Where Mi=3)
 Set 2: Each nurse works only one shift a day:
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints
….“n” equations
….“n” equations
….“n” equations
….“n*m” equations

13. 13
Hard Constraints:
 Set 3: Avoid any isolated days patterns of “off-on-off” :
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
….“(n-2)*m” equations
Day1 Day2 Day3
Off On Off
C1 X2/Y2/Z2 C3 Sum
Unacceptable
1 1 1 3
Acceptable
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 2
1 0 0 1
1 0 1 2
1 1 0 2
Yes
No

14. 14
Hard Constraints:
 Set 4: Each nurse works 3 consecutive days of night shift and followed by 3 days
off. Each nurse will be assigned to their night shifts and off days as follow:
13.04.1414Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
….“m” equations

15. 15
Hard Constraints:
 Set 5: Each nurse works between 12 to 14 days per schedule:
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
….“2*m” equations
For each Nurse total Sum of all working
shift should lie between 12 & 14

16. 16
Hard Constraints:
 Set 6: Each nurse works not more than 6 consecutive days:
 Each Nurse has to have at least 1 “Off” in 7 consecutive days
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
Cases for 7 Consecutive days for Kth Nurse
Case-
1
Case-
2
Case-
3
Case-
4
Case-
5
Case-
6
Case-
7
Case-
8
Case-
9
Case-
10
Case-
11
Case-
12
Case-
13
Case-
14
Case-
15
Case-
16
Case-
17
Case-
18
Case-
19
Case-
20
Case-
21
Days
1 K K+1 K+1 K+1 K+1 K+1 K+1
2 K K K+1 K+1 K+1 K+1 K+1
3 K K K K+1 K+1 K+1 K+1
4 K K K K K+1 K+1 K+1
5 K K K K K K+1 K+1
6 K K K K K K K+1
7 K K K K K K K
8 K K K K K K K
9 K K K K K K K
10 K K K K K K K
11 K K K K K K K
12 K K K K K K K
13 K K K K K K K
14 K K K K K K K
15 K K K K K K K
16 K K K K K K K
17 K K K K K K K
18 K K K K K K K
19 K K K K K K K
20 K K K K K K K
21 K K K K K K K
7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7
Due to Cyclic
constraint, Nurse “K”
has to take position of
“K+1” in each next cycle

17. 17
 Set 6: Each nurse works not more than 6 consecutive days
 For 1st 15 Days, 18 Nurses (in following eq “i” can take maximum of 15 value)
 For next 6 days, 17 Nurses (in following eq “k” can take maximum of 17 value)
 For next 6 days, 18th Nurses
13.04.1417Nurse Scheduling-IGP 13.04.1417Nurse Scheduling-IGP
6
….“(n-6)*m” equations
Problem Formulation-Constraints (continued..)
….“6*(m-1)” equations
….6 equations

18. 18
 Set 7: Evening shift constitutes at least 25% of total workload:
 Sum of all Evening shifts for a nurse >=25% of Total worked shifts
 Set 8: Morning shift constitutes at least 30% of total workload:
o Sum of all Morning shifts for a nurse >=30% of Total worked shifts
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
0.25* ….“m” equations
0.30* ….“m” equations

19. 19
Soft Constraints:
 Soft constraints are arising out of Nurses’ preferences so these can be treated as Goals for our Integer
Liner Programming.
 The deviation for each goal are christened:
 ρ : Positive Deviation
 η : Negative Deviation
 Set 1: Avoid working in an evening shift followed by a morning shift or a night
shift the next day:
13.04.14Nurse Scheduling-IGP
Day1 Day2
Evening Morning/Night
Y1 X2/Z2 Sum
Unacceptable
1 1 2
Acceptable
0 0 0
0 1 1
1 0 1
Yes No
Problem Formulation-Constraints (continued..)

20. 20
 Set 1: Avoid working in an evening shift followed by a morning shift or a night
shift the next day:
 For 1st 20 Days, 18 Nurses (in following eq “i” can take maximum of 20 value)
 For 21st & 1st days, 17 Nurses (in following eq “k” can take maximum of 17 value)
 For 21st & 1st days, 18th & 1st Nurses
13.04.14Nurse Scheduling-IGP 13.04.14Nurse Scheduling-IGP
….“(n-1)*m” equations
Problem Formulation-Constraints (continued..)
….“(m-1)” equations
….1 equation
Goal-1: Minimize
=
=
=

21. 21
 Set 2: Avoid working in an Morning shift followed by a Evening shift or a night
shift the next day:
 For 1st 20 Days, 18 Nurses (in following eq “i” can take maximum of 20 value)
 For 21st & 1st days, 17 Nurses (in following eq “k” can take maximum of 17 value)
 For 21st & 1st days, 18th & 1st Nurses
13.04.14Nurse Scheduling-IGP 13.04.14Nurse Scheduling-IGP
….“(n-1)*m” equations
Problem Formulation-Constraints (continued..)
….“(m-1)” equations
….1 equation
Goal-2: Minimize
=
=
=

22. 22
 Set 3: Each nurse has at least one weekend off:
 Sum of above heighted weekends >=1 (for each Nurse)
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
Nurse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Days
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Each Nurse has to have at least one
Off here out of highlighted 3
weekends
….“m” equations
Goal-3: Minimize
=

23. 23
 Set 4: All nurses have the same amount of total workload:
 In Hard Constraint Set-5, it has been seen that Management preference for total work
load should be between 12 & 14.
 But Nurses prefer to have equal work load.
 Thus trade off is to have work load of 13 for each nurse.
Sum of all shifts for each Nurse = 13
13.04.14Nurse Scheduling-IGP
Problem Formulation-Constraints (continued..)
….“m” equations
Goal-4: Minimize
Binary Constraints:
For each nurse and for each shift (Morning, Evening, Night, Off), value can be
either 1 or 0.

24. 24 13.04.14Nurse Scheduling-IGP
Problem Formulation-Objective Function:
Preemptive Goal Programming for this model:
Subject to:
• Hard constraints
• Soft constraints
• Binary Constraints
• Non-negativity constraints

25. 25
Programming in LINGO
13.04.14Nurse Scheduling-IGP
Defining Sets
Import & Export of
Data with Excel

26. 26
Program Execution
13.04.14Nurse Scheduling-IGP

27. 27
Time Line Analysis
13.04.14Nurse Scheduling-IGP
1 2 3 4 5 6 7 8
No of Nurses 5 6 7 8 9 10 11 12
Time to Solve (min) 16 19 81 134 212 901 1498 3980
0
500
1000
1500
2000
2500
3000
3500
4000
4500
Timetosolve(inMinutes)
No. of Variables Vs Time to solve
(for 21 Days)
Exponential
increase in
time to solve
the problem
w.r.t. No. of
Nurses

28. 28
Result-Optimal Solution
13.04.14Nurse Scheduling-IGP
OVERALL SCHEDULE
Nurse Total
Nurses in
Morning
Shift
Total
Nurses in
Evening
Shift
Total
Nurses in
Night Shift
Total
Nurses
in all
Shifts1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Days
1 N OFF OFF OFF E E N OFF M E E M N OFF M M OFF OFF 4 4 3 11
2 N OFF M OFF E E N OFF E E OFF OFF N OFF M M M OFF 4 4 3 11
3 N OFF M OFF E OFF N OFF OFF E M OFF N OFF E E M M 4 4 3 11
4 OFF E E E OFF N OFF M M OFF E N OFF M OFF OFF M N 4 4 3 11
5 OFF E E E M N OFF E M M OFF N OFF M OFF OFF OFF N 4 4 3 11
6 OFF E E OFF M N OFF E OFF M OFF N OFF M E OFF M N 4 4 3 11
7 E E OFF M N OFF OFF E M OFF N OFF M M E OFF N OFF 4 4 3 11
8 E E M M N OFF OFF OFF M OFF N OFF E E E M N OFF 4 5 3 12
9 OFF E E M N OFF M M OFF OFF N OFF E E OFF M N OFF 4 4 3 11
10 E OFF E N OFF OFF M M E N OFF M OFF OFF M N OFF E 4 4 3 11
11 E M OFF N OFF OFF E M E N OFF M OFF E M N OFF E 4 5 3 12
12 OFF M OFF N OFF M E M OFF N OFF M E E OFF N OFF E 4 4 3 11
13 OFF M N OFF M M OFF E N OFF M E E OFF N OFF OFF E 4 4 3 11
14 OFF M N OFF M E E E N OFF M OFF OFF M N OFF OFF E 4 4 3 11
15 E OFF N OFF OFF E E OFF N OFF M E M M N OFF M OFF 4 4 3 11
16 E N OFF E M OFF OFF N OFF M E E M N OFF M E OFF 4 5 3 12
17 OFF N OFF E M M OFF N OFF E OFF E OFF N OFF M E M 4 4 3 11
18 M N OFF OFF E M M N OFF E M OFF OFF N OFF E OFF E 4 4 3 11
19 N OFF OFF M OFF M N OFF M E E OFF N OFF M E E OFF 4 4 3 11
20 N OFF E M OFF OFF N OFF E OFF E M N OFF M OFF E M 4 4 3 11
21 N OFF E E OFF M N OFF OFF M OFF M N OFF OFF E E M 4 4 3 11
Total Morning Shifts 1 4 3 5 6 6 3 5 6 4 5 6 3 6 6 6 5 4
Total Evening Shifts 6 6 7 5 4 4 4 5 4 6 5 4 4 4 4 4 5 6
Total Night Shifts 6 3 3 3 3 3 6 3 3 3 3 3 6 3 3 3 3 3
Total Off's 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8
Total Working Days 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13
Hard Constraints
1) Demand is met
2) Each nurse
works at most one
shift a day
3) Avoid any isolated days
patterns of “off-on-off”.
4) Each nurse must
have three days off
after having three
consecutive night
5) Each nurse
works between 12
to 14 days per
schedule.
6) Each nurse works
not more than 6
consecutive days
7) Evening shift
constitutes at least 25%
of total workload
Soft Constraints
1) Avoid working in an evening shift
followed by a morning shift or a
nightshift the next day
3) Each nurse has at
least one day off in one
weekend.
4) All nurses have the
same amount of total
workload

29. 29
Conclusion
Achievements
 The developed model with various constraints and goals using the 0-1 goal programming
technique gives the optimum solution that showed both the hard constraints and soft
constraints are satisfied.
 The pattern will be rotated among the nurses and each nurse will be working according to
each schedule’s pattern. After completing 18 schedules, then each nurse will revisit the
starting schedule.
 Cyclical nurse scheduling rotates equally through the desirable and undesirable work
stretches among the nurses and requires relatively less scheduling effort of the head nurse.
 The schedule satisfies the factors of completeness and continuity. While the fairness factor is
dealt with since the schedule’s pattern is going to rotate among the nurses.
 All nurses will have the opportunity to work with the satisfactory and unsatisfactory
schedule’s patterns.
 With this cyclical scheduling, it gives nurses more control over their work life because they
know the type of shift schedule in the future which should have a positive effect on their job
satisfaction.
13.04.14Nurse Scheduling-IGP

30. 30
The way forward
 New schedule will only need to be produced when changes occur in its average daily staff
requirements.
 For further research, one of possible work is to embed the model into user friendly software that
would be easy to use and reliable.
 The model also should be extended to account for other important scheduling aspects such as
requested day off in order to being acceptable to all parties.
Applications
 Transportation
 Call centres
 Health care
 Emergency services
 Civic services and utilities
 Venue management
 Financial services
 Hospitality and tourism
 Manufacturing
13.04.14Nurse Scheduling-IGP
Conclusion (continued..)

31. HEALTH CENTRE, IIS c
13.04.14Nurse Scheduling-IGP
PILOT STUDY- NURSE SCHEDULING
31
Photo courtesy: Ms. D. Choudhary

32. 32
Pilot Study at Health Centre IISc
13.04.14Nurse Scheduling-IGP
Number of Nurses 11
Number of Days 14 (2 Weeks)
Number of Shifts: 3 (Morning, Day & Night)
Number of Decision Variables 11 X 14 X 4 (3 shifts+1 Off) = 616
Type of Decision Variables Binary (0-1)
Health Centre 11 nurses 3 Shifts
Morning Shift
At least 5
nurses
Evening Shift
At least 2 nurses
Night Shift
Exactly 1 nurses
6:00 am-1:00pm
1:00pm-8:00pm
8:00pm-6:00am

33. 33 13.04.14Nurse Scheduling-IGP
Constraints
• Hard Constraints (Management)
• Soft Constraints (Nurse Specific)
Hard
Constraints
• Each unit is covered by 3 shifts for 24 hours a day and 7 days a week.
• Minimum staff level requirement must be satisfied.
• Each nurse works at most one shift a day.
• Each nurse works not more than 6 consecutive days.
• Each nurse can’t have more than 3 holidays fortnightly.
Soft
Constraints
• Avoid working in Night shift followed by Morning shift or Evening shift of the next day.
• Each nurse has at least one day off in one weekend. (could not be met)
Problem Formulation-Constraints Description
Hard Constraints-Must be satisfied
Soft Constraint-May be violated
Goal
Programming

34. 34
Execution & Result
13.04.14Nurse Scheduling-IGP
OVERALL SCHEDULE PROPOSED FOR HEALTH CENTRE, IISc
Nurses Total
Nurses in
Morning
Shift
Total
Nurses in
Evening
Shift
Total
Nurses in
Night Shift
Total
Nurses
in all
Shifts1 2 3 4 5 6 7 8 9 10 11
Days
1 E E M M M N M E M E E 5 5 1 11
2 E M E E M N M E E M M 5 5 1 11
3 M N M E OFF OFF OFF M M M E 5 2 1 8
4 M N OFF E M E M OFF OFF M M 5 2 1 8
5 M OFF E E M E E N M M M 5 4 1 10
6 OFF E M OFF E M M N M M OFF 5 2 1 8
7 OFF M M E OFF M E N M OFF M 5 2 1 8
8 M M OFF N E OFF M OFF M M E 5 2 1 8
9 E M M OFF M E OFF N OFF M M 5 2 1 8
10 M N M E M E M OFF M E OFF 5 3 1 9
11 N OFF M M E M E M E OFF M 5 3 1 9
12 N E M M OFF M OFF E M M M 6 2 1 9
13 OFF N E OFF M E M M E M M 5 3 1 9
14 M OFF OFF M M E M M OFF E N 5 2 1 8
Total Morning Shifts 6 4 8 4 8 4 8 4 8 9 8
Total Evening Shifts 3 3 3 6 3 6 3 3 3 3 3
Total Night Shifts 2 4 0 1 0 2 0 4 0 0 1
Total Off's 3 3 3 3 3 2 3 3 3 2 2
Total Working Days 11 11 11 11 11 12 11 11 11 12 12
Hard Constraints
1) Demand is met
2) Each nurse works at
most one shift a day
3) Each nurse works not more
than 6 consecutive days
4) Each nurse can’t have more
than 3 holidays fortnightly
Soft Constraints
1) Avoid working in Night shift followed by
Morning shift or Evening shift of the next day

35. 35 13.04.14Nurse Scheduling-IGP
Websites
 www.lindo.com
 www.journal.itb.ac.id
Research Papers
 A Cyclic Nurse Schedule using Goal Programming By Ruzzakiah Jenal et.al.
 A Multiple Objective Nurse Scheduling Model By Arthur & Ravidran
 Scheduling Nurses Using Goal-Programming Techniques By Musa & Saxena
 Goal Programming Model Subsystem of A Flexible Nurse Scheduling Support System By
Ozkarahan & Bailey
Books
 An Introduction to Management Science By Anderson Sweeney Williams
Tools used
 Microsoft Encarta (Encyclopedia for offline references)
 Microsoft Excel (Data embedding)
 Industrial LINGO (Linear Integer Programming)
References

36. 13.04.14Nurse Scheduling-IGP 36
Thank you!
They said it….
“There’s a fundamental distinction between strategy and operational effectiveness”
(Michael Porter)
Leanings….
• Practical application of Operations Research
• Optimization Software- LINGO and its limitations
• Literature Review of Research Paper