1) The document discusses Fisher's linear discriminant analysis (LDA) and how it can be implemented using NumPy. 2) LDA aims to find the vectors that best discriminate between classes of objects. It calculates a linear combination of features that separates cases into categories. 3) The document provides code to load iris data, calculate the within-class and between-class scatter matrices W and B, and derive the projection matrix X by taking the inverse of W and multiplying it by B. It then computes the eigenvalues and eigenvectors of X.

1. NUMPY
- -
gerumanium3_2

2. .....

3. https://gist.github.com/
gerumanium

4. twitter
ID gerumanium3_2

5. numpy

7. (Pattern Recognition)

8. :
:

10. Discriminant Analysis
z
Fisher (FDA)
(discrimination)
(classification)
(LDA)
(QDA)

11. 1. -
2.

12. fisher(1890 1962)

13. 1. W
B
−1
2. X =W B
3. X λ
4. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4

14. x1:
x2:
x3:
x4:
L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4
L ” L ” l1 , l2 , l3 , l4

15. K
W = Sk
L k=1
W T B Sk = (xn − mk )(xn − mk )T
n∈Ck
1
W: mk = xn
Nk
n∈Ck
T: N
B: T = (xn − mn )(xn − m)T
m=1
T =W +B

16. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4
l Bl
Q≡ → max
l Wl
L
l’Bl l’Wl

17. Q L
−1
X=W B
X λ
l1 , l2 , l3 , l4

18. 1. W
B
−1
2. X =W B linalg.inv()
3. X λ
linalg.eig()
4. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4

19. numpy

20. numpy
python
numpy
“iris.txt”

21. >>from numpy import *
>>data=loadtxt("iris.txt")
>>

22. >>>#
>>>Vi=array([data[i] for i in range(0,50)])
>>>#Vi Vi.T transpose(Vi)
>>>Vi=Vi.T
>>>Vi=array([Vi[i] for i in range(1,5)])
>>>
 
x 1
x2 
x = x1 , x2 , x3 , x4 , x5 →x= 
x3 
x4

23. >>#
>>Ve=array([data[i] for i in range(50,100)])
>>Ve=Ve.T
>>Ve=array([Ve[i] for i in range(1,5)])
>>
>>#
>>Se=array([data[i] for i in range(100,150)])
>>Se=Se.T
>>Se=array([Se[i] for i in range(1,5)])
>>

24. >>> #
>>> data=data.T
>>> #(4,150)
>>> data=array([data[i] for i in range(1,5)])
>>>

25. 1. W
B
−1
2. X =W B linalg.inv()
3. X λ
linalg.eig()
4. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4

26. 1. W
B

27. 3
W = Sk
k=1
= (V in − V¯i)(V in − V i)T
¯
n∈V i
+ (V en − V¯e)(V en − V¯e)T
n∈V e
+ ¯ ¯ T
(Sen − Se)(Sen − Se)
n∈Se

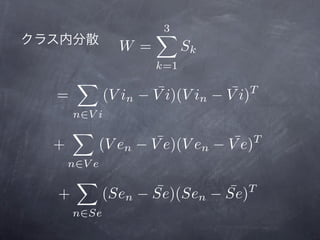
28. >W=zeros((4,4))
>#Vi
>m1=array([[mean(i) for i in Vi]])
>m1=m1.T
>W+=dot(Vi-m1,transpose(Vi-m1))
(V in − V¯i)(V in − V i)T
¯
n∈V i

29. #Ve
>m2=array([[mean(i) for i in Ve]])
>m2=m2.T
>W+=dot(Ve-m2,transpose(Ve-m2))
>
(V en − V¯e)(V en − V¯e)T
n∈V e

30. #Se
>m3=array([[mean(i) for i in Se]])
>m3=m3.T
>W+=dot(Se-m3,transpose(Se-m3))
¯ ¯ T
(Sen − Se)(Sen − Se)
n∈Se

31. T
N
T
T = (xn − x)(xn − x)
¯ ¯
n=1
B=T−W

32. >>#
>>M=array([[mean(i) for i in
data]]).T
>>T=dot(data-M,transpose(data-M))
#
>>B=T-W
>>

33. 1. W
B
2. −1 linalg.inv()
X=W B
3. X λ
linalg.eig()
4. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4

34. >># linalg.inv()
>>X=dot(linalg.inv(W),B)
>>

35. 1. W
B
−1
2. X =W B linalg.inv()
3. X λ
linalg.eig()
4. L = l 1 x 1 + l 2 x 2 + l 3 x 3 + l4 x 4

36. >>>#
>>>#la
>>>#v la
>>>la,v = linalg.eig(X)
>>> la
array([3.21919292e
+01,2.85391043e-01,
3.25093377e-15,
3.08736744e-14])
>>>

37. (1)
L = −0.20874182x1
−0.38620369x2
+0.55401172x3
+0.7073504x4

38. L ( L(1) L(x) )
(2) (1)
L = −0.20874182x1 L = −0.20874182x1
−0.38620369x2 −0.38620369x2
+0.55401172x3 +0.55401172x3
+0.7073504x4 +0.7073504x4

40. <http://d.hatena.ne.jp/
gerumanium/> ...

41. R
5 (2009)
(2007)
(2008)