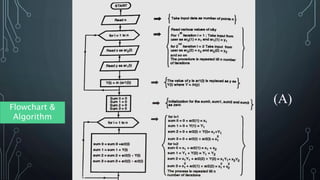
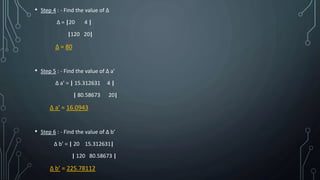
This document provides an algorithm and flowchart for fitting an exponential curve to data using the equation y = aebx. It involves the following steps: 1. Convert the equation to linear form by taking the log of both sides as ln(y) = ln(a) + bx 2. Create a table with the x, y, ln(y), x2, and xy values 3. Derive equations to solve for the coefficients a' and b' 4. Calculate the necessary deltas and ratios to determine the values of a' and b' 5. Substitute the coefficient values back into the original exponential equation to obtain the best-fit curve.

1. EXPONENTIAL EQUATION (y = aebx) FITTING :-
ALGORITHM, FLOWCHART AND NUMERICAL
Presented by,
VAIBHAV SANJAY
PATIL
TEME – A – 13
(CIA – 3)
Guided by,
Prof. D.R. Satpute

2. Flowchart &
Algorithm
(A)

3. (B)

4. * Fill the exponential curve y = aebx to the following data
• Step 1 : - Convert the equation into y = ax + b form
To find out the values of a & b we require here to prepare a table as below. The equation being
y = aebx
Taking loge both sides i.e.
In y = In a + bx In (e) since In (e) = 1
We get In y = In a + bx
Y = a’x + b’
Where Y = In y
a’ = b
b ’ = In a
X 2 4 6 8
Y 25 38 56 84

5. • Step 2 : - Prepare the table indicating the value of ΣX, ΣY, ΣX2, ΣXY
• Step 3 : - Write the desired equation for straight line
Σy = A Σx + nB
15.312631 = 20(A) + 4(B) ……………………………………………………(1)
Σxy = A Σx2 + B Σx
80.58673 = 120(A) + 20(B) ………………………….………………………….(2)
x y Y xy x2
2
4
6
8
25
38
56
84
3.218876
3.637586
4.025352
4.430817
3.43775
14.55034
24.15211
35.44653
4
16
36
64
Σx = 20 ΣY=15.312631 Σxy=80.58673 Σx2 = 120

6. • Step 4 : - Find the value of Δ
Δ = |20 4 |
|120 20|
Δ = 80
• Step 5 : - Find the value of Δ a’
Δ a’ = | 15.312631 4 |
| 80.58673 20|
Δ a’ = 16.0943
• Step 6 : - Find the value of Δ b’
Δ b’ = | 20 15.312631|
| 120 80.58673 |
Δ b’ = 225.78112

7. • Step 7 : - Then the bet curve is given by the equation
 ∴ a‘ = Δ a’ ÷ Δ
= 16.0743 ÷ 80
a’ = 0.201178
b’ = Δ b’ ÷ Δ
= 225.78112 ÷ 80
b’ = 2.822264
∴ Δ b’ = Δ a’ = 0.201178
a = Antilog b’ = 16.81488
∴ The equation becomes
y = 16.81488 e0.201178 x

8. THANK YOU…..