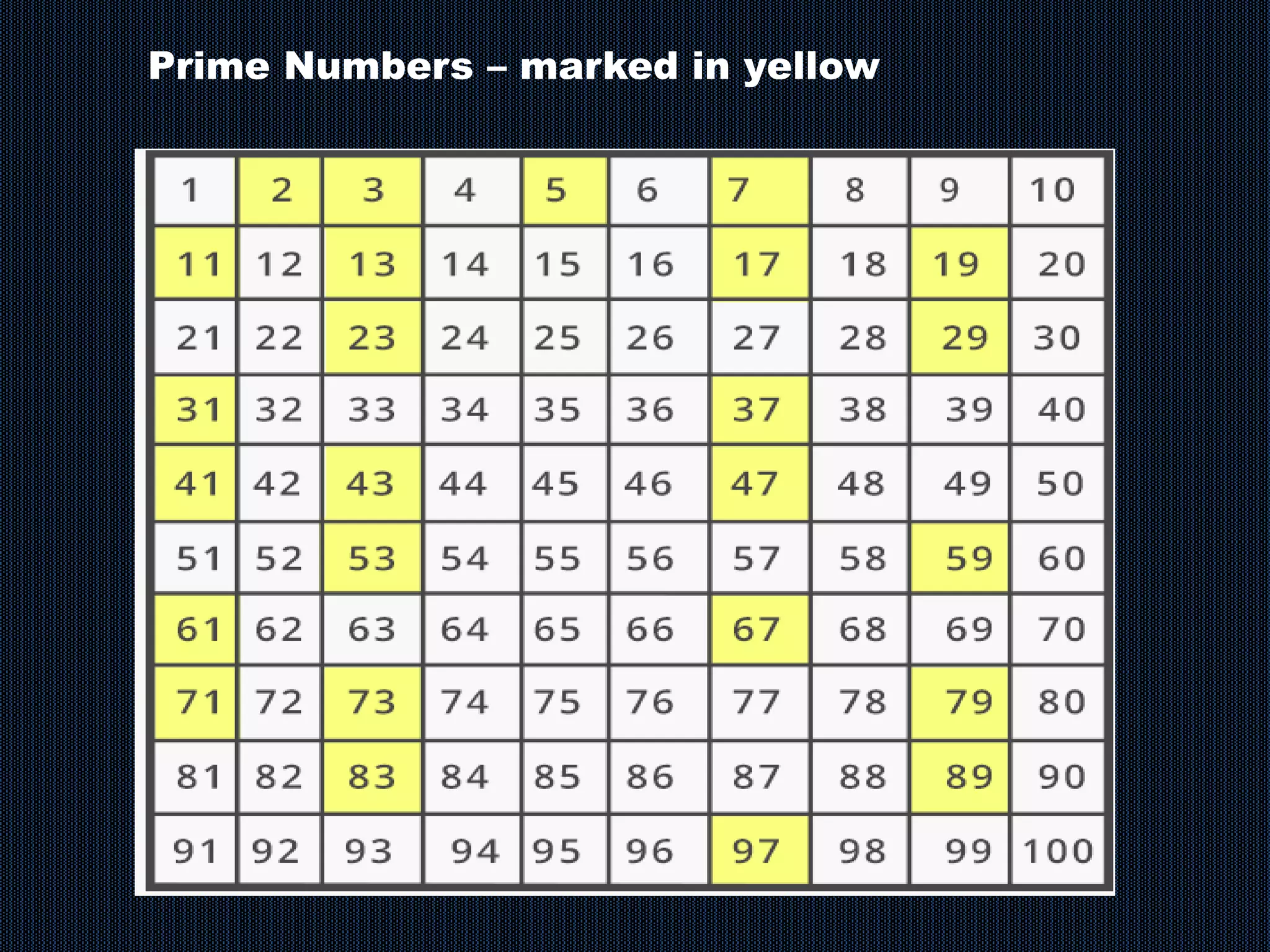
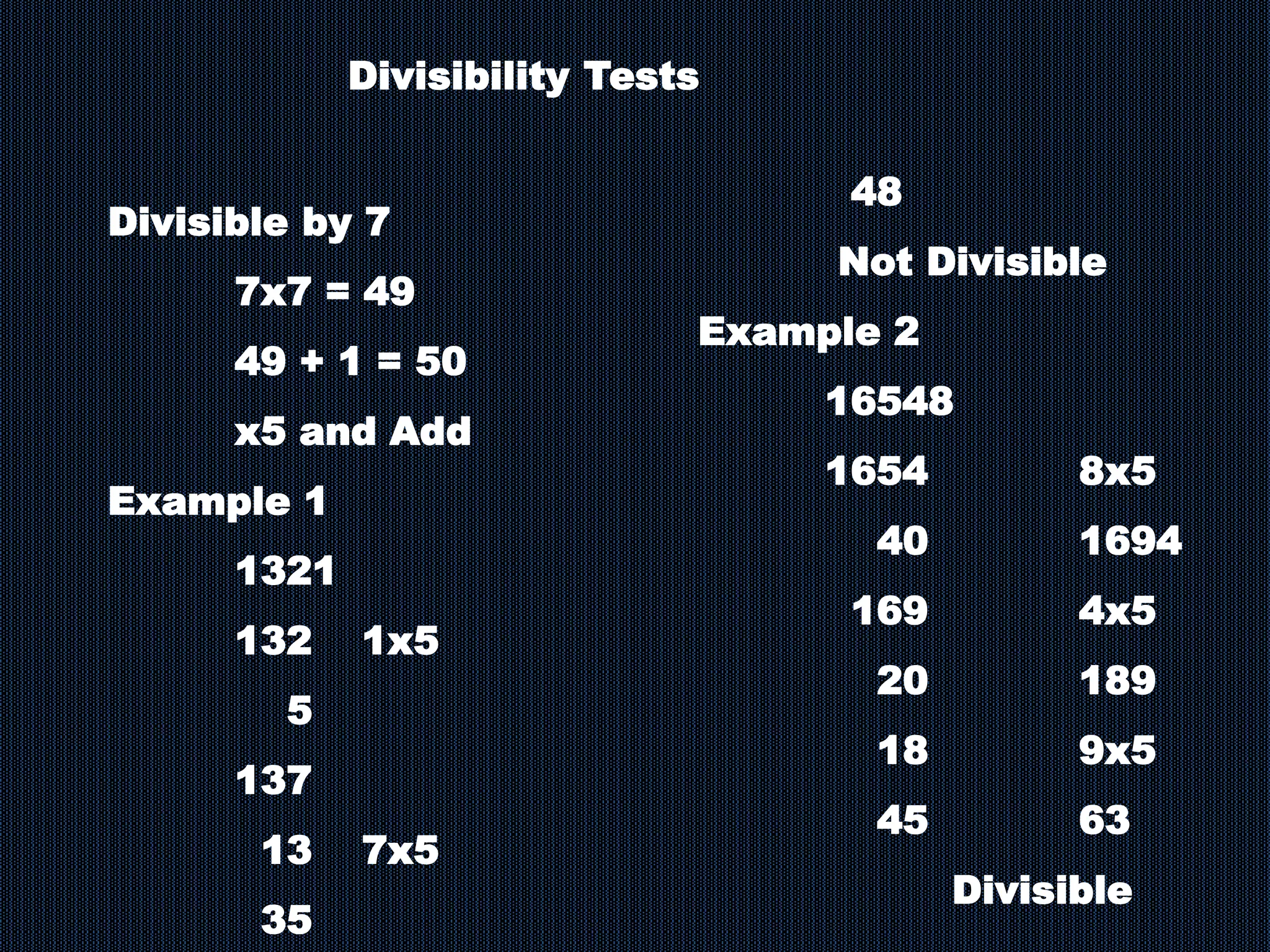
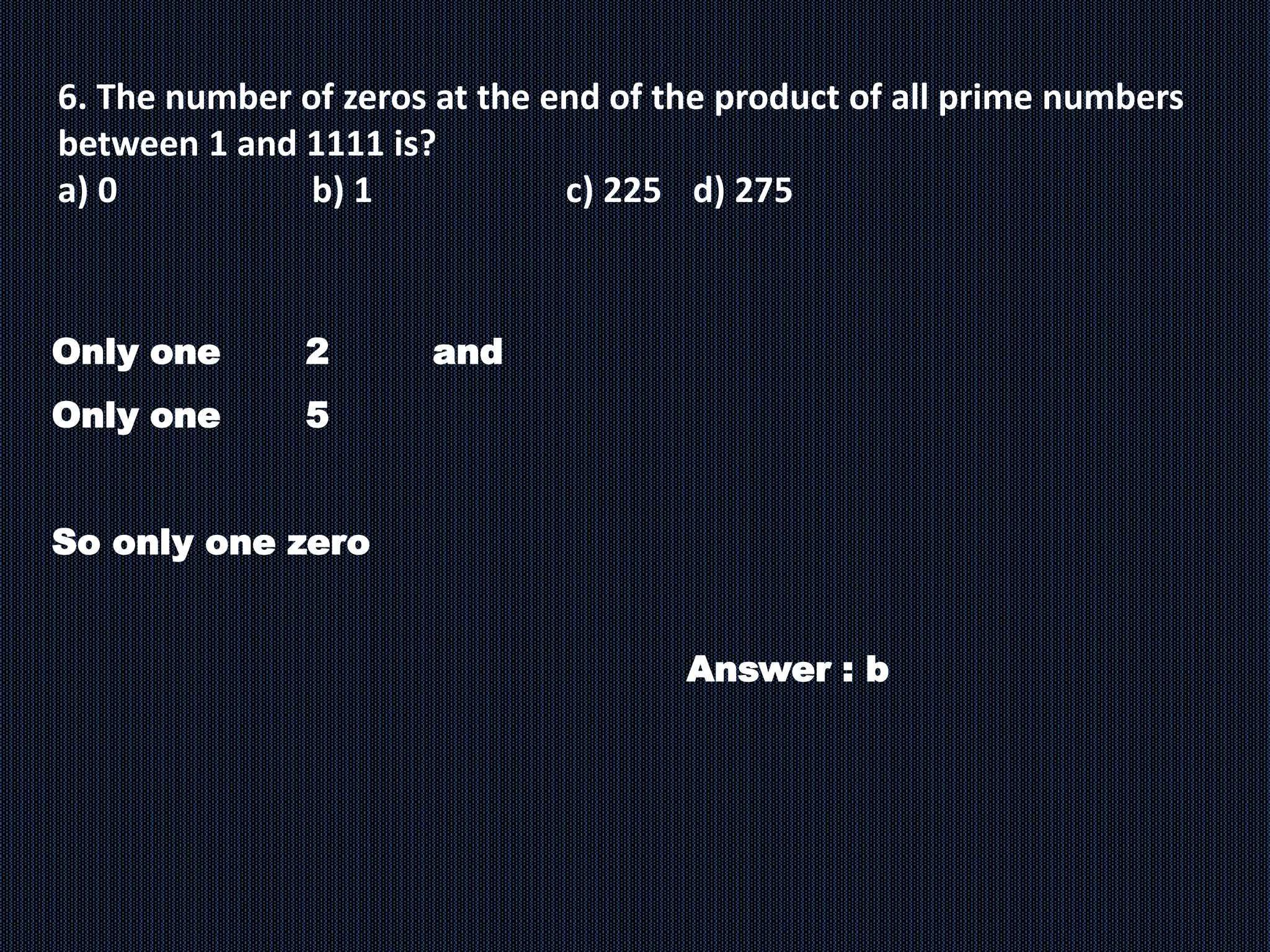
The document discusses various concepts related to numbers including positive integers, prime numbers, composite numbers, and divisibility tests. It provides definitions and examples of prime numbers, composite numbers, and tests for divisibility by numbers from 2 to 18. The divisibility tests covered include divisibility by sums of digits, last digits, and performing operations on digits. Examples are provided to demonstrate the divisibility tests.

1. 18PDH101T
General Aptitude

2. Numbers

4. Positive Integers
Non – Negative Integers
- Natural Numbers
- Whole Numbers
Prime Numbers
- Divisible by 1 and by the number itself
- Only 2 factors
2, 3, 5, 7, 11, 13, 17, 19 . . .
Composite Numbers
- Except Prime Numbers
1 – Neither Prime nor Composite
2 – Only Even Prime number

5. Prime Numbers – marked in yellow

7. Divisibility Tests
Divisible by 2
- All even numbers
- Numbers end with 0, 2, 4, 6, 8
Divisible by 3
- Sum of the digits divisible by 3
Example –
176
1 + 7 + 6 = 14 not divisible
24871
2 + 4 + 8 + 7 + 1 = 22 not divisible
14913
1 + 4 + 9 + 1 + 3 = 18 divisible

8. Divisibility Tests
Divisible by 4
- last 2 digits divisible by 4
Example –
226 - 26 / 4 not divisible
1248 - 48 / 4 divisible
Divisible by 5
- Last digit 0 or 5
Divisible by 6
- Divisible by both 2 and 3

9. Divisibility Tests
Divisible by 8
- last 3 digits divisible by 8
Example –
12226
226 / 8 not divisible
21248
248 / 8 divisible

10. Divisible by 9
- Sum of the digits divisible by 9
Example –
176
1 + 7 + 6 = 14 not divisible
24871
2 + 4 + 8 + 7 + 1 = 22 not divisible
14913
1 + 4 + 9 + 1 + 3 = 18 divisible
Divisible by 10
- Last digit 0
Divisibility Tests

11. Divisibility Tests
Divisible by 11
- The difference between Sum of odd terms
and even terms = 0 or divisible by 11
Example
156348
1 + 6 + 4 = 11
5 + 3 + 8 = 16
Difference = 16 – 11 = 5
not divisible

12. Divisibility Tests
Divisible by 7
7x7 = 49
49 + 1 = 50
x5 and Add
Example 1
1321
132 1x5
5
137
13 7x5
35
48
Not Divisible
Example 2
16548
1654 8x5
40 1694
169 4x5
20 189
18 9x5
45 63
Divisible

13. Divisibility Tests
Divisible by 13
13x3 = 39
39 + 1 = 40
x4 and Add
Divisible by 17
17 x 3 = 51
51 – 1 = 50
x5 and Subtract

14. Divisible by 12
- Divisible by both 3 and 4
To select 2 numbers to check divisibility
- Product should be the original number
- The numbers should be co – prime
Divisible by 18
- Divisible by 2 and 9
Divisible by 24
- Divisible by 3 and 8
Divisibility Tests

15. Divisible by 35
- Divisible by 5 and 7
Divisible by 36
- Divisible by 4 and 9
Divisibility Tests

16. 1. What is the minimum number to be added to make
329611 as divisible by 6
a) 1 b) 3 c) 5 d) 7
divisible by 6
divisible by 2 and 3
/3
3 + 2 + 9 + 6 + 1 + 1
= 22
From options
a 22 + 1 = 23 not divisible
b 22 + 3 = 25 not divisible
c 22 + 5 = 27 divisible
/2
329611 + 5 = 329616
even number
so divisible by 2
Answer : c

17. 2. 1358k24679 is divisible by 11. Find the value of k
a) 0 b) 1 c) 4 d) 9
divisible by 11
1358k24679
1 + 5 + k + 4 + 7 =
3 + 8 + 2 + 6 + 9 =
28 – (17 + k) = 0 or divisible by 11
so k = 0
answer : a
17 + k
28

18. 3. 4231k4 is divisible by 24. Find the value of k
a) 7 b) 4 c) 6 d) 1
divisible by 24
- divisible by 3 and 8
4 + 2 + 3 + 1 + k + 4 = 14 + k
from options
a 14 + 7 = 21 divisible by 3
174 / 8 not divisible by 8
b 14 + 4 = 18 divisible by 3
144 / 8 divisible by 8
answer : b

19. 4.11564k4 is divisible by 36. Find the value of k
a) 6 b) 2 c) 9 d) 7
divisible by 36
- divisible by 4 and 9
1 + 1 + 5 + 6 + 4 + k + 4 = 21 + k
from options
a 21 + 6 = 27 divisible by 9
64 / 4 = 16 divisible by 4
answer : a

20. 5. 996ab is divisible by 80. What is (a + b) ?
a) 3 b) 5 c) 6 d) 8
divisible by 80
996ab
b must be 0
996a is divisible by 8
Option a and b 3 & 5 odd numbers
not divisible by 8
option c 966 / 8
not divisible by 8
so a = 8 968 / 8 divisible by 8
a = 8 ; b =0 a + b = 8
answer : d

21. 6. 477 is not divisible by
a) 53 b) 3 c) 6 d) 9
477 is odd number
not divisible by 6
477 / 53 = 9 divisible by 53
4 + 7 + 7 = 18 divisible by 3 and 9
answer : c

22. 7. The product of 4 consecutive even numbers is
always divisible by:
a) 600 b) 768 c) 864 d) 384
Product of first 4 consecutive even numbers
= 2 * 4 * 6 *8
= 384
answer : d

23. 8. What is the largest 4 digit number exactly divisible
by 88?
a) 9944 b) 9999 c) 9988 d) 9900
Divisible by 88
- Divisible by 8 and 11
all 4 options divisible by 11
a 944 / 8 = 118 divisible by 8
b odd number not divisible by 8
c 988 / 8 not divisible by 8
answer : a

24. (a^n) – (b^n)
is divided by (a-b) for ∀n∈ N
is divided by(a+b) for all even integers of N
(a^n) + (b^n)
is divisible by (a+b) for all odd integers of N
9. Which of the following numbers will completely
divide ((49^15) - 1) ?
a) 11 b) 7 c) 8 d) 9
((49^15) - 1) = (7^30) – 1
It is divisible by 7+1
8

25. 10. It is being given that (232 + 1) is completely divisible
by a whole number. Which of the following numbers is
completely divisible by the number?
a) (216 + 1) b) (216 - 1) c) (7 x 223) d) (296 + 1)
(296 + 1) = (232 ) 3+ 1
So Its divisible by (296 + 1)

26. Unit Digit
Find the unit digit of the sum
263 + 541 + 275 + 562 + 758
Add only the unit digits
= 19
Unit digit = 9
Find the unit digit of the product
543 * 548 * 476 * 257
Multiply only unit digits
unit digit = 8

27. Unit Digit
what is the unit digit of
1237 - 4563 + 6214 + 8541 - 5612
a) 5 b) 3 c) 8 d) 7
Answer : d
Find the unit digit of the product
567 x 142 x 263 x 429 x 256
a) 5 b) 3 c) 8 d) None of these
Answer : c
Find the unit digit of product of the prime numbers up to 50.
a) 0 b) 1 c) 2 d) 5
2 * 3 * 5 * …
= 0
Answer : a

28. Unit digit of 2^ 156 = ?
2^1 = 2
2² = 4
2³ = 8
2⁴ = 16
Unit Digit
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
Unit digit of 2^ any number is one among
2, 4, 8 and 6
Divide the power by 4
If divisible unit digit 2⁴ = 6
If remainder 1 unit digit 2^1 = 2
If remainder 2 unit digit 2² = 4
If remainder 3 unit digit 2³ = 8
Unit digit of 2^ 156
56 / 4
divisible
so unit digit is 6

29. 3^1 = 3
3² = 9
3³ = 27
3⁴ = 81
Unit Digit
Unit digit of 3^ any number is one among
3, 9, 7 and 1
Divide the power by 4
If divisible unit digit 3⁴ = 1
If remainder 1 unit digit 3^1 = 3
If remainder 2 unit digit 3² = 9
If remainder 3 unit digit 3³ = 7

30. 4^1 = 4
4² = 16
4³ = 64
4⁴ = 256
Unit Digit
Unit digit of 4^ any number is 4 or 6
If the power is odd number
Unit digit is 4
If the power is even number
Unit digit is 6
5^1 = 5
5² = 25
5³ = 125
Unit digit is always 5
6^1 = 6
6² = 36
6³ = 216
Unit digit is always 6

31. 7^1 = 7
7² = 49
7³ = __3
7⁴ = __1
Unit Digit
Unit digit of 7^ any number is one among
7, 9, 3 and 1
Divide the power by 4
If divisible unit digit 7⁴ = 1
If remainder 1 unit digit 7^1 = 7
If remainder 2 unit digit 7² = 9
If remainder 3 unit digit 7³ = 3

32. 8^1 = 8
8² = 64
8³ = __2
8⁴ = __6
Unit Digit
Unit digit of 8^ any number is one among
8, 4, 2 and 6
Divide the power by 4
If divisible unit digit 8⁴ = 6
If remainder 1 unit digit 8^1 = 8
If remainder 2 unit digit 8² = 4
If remainder 3 unit digit 8³ = 2

33. 9^1 = 9
9² = 81
9³ = __9
9⁴ = __1
Unit Digit
Unit digit of 9^ any number is 9 or 1
If the power is odd number
Unit digit is 9
If the power is even number
Unit digit is 1
1^1 = 1
1² = 1
1³ = 1
Unit digit is always 1
0^1 = 0
0² = 0
0³ = 0
Unit digit is always 0

34. Unit Digit
2, 3, 7 and 8
Divide the power by 4
4 and 9
Power odd / even number
0, 1, 5 and 6
The number itself

35. 1. What is the digit in the unit place of the number
represented by
(79^5 – 35^8)?
a) 4 b) 3 c) 2 d) 1
(79^5 – 35^8)
9^5 - 5^8
=
= 4
9^5
Power is odd number
So Unit digit is 9
5^8
Unit digit is 5
9 5
-
Answer : a

36. 2. Find the unit digit of
352^4 + 43^24 + 4137^ 754 + 689 ^ 561
a) 5 b) 6 c) 7 d) 8
352^4 + 43^24 + 4137^ 754 + 689 ^ 561
= 2^4 + 3^24 + 7^ 754 + 9 ^ 561
=
2^4 = 16 unit digit 6
3^24 Divide the power by 4
24 / 4 divisible
So 3^4 Unit digit 1
7^ 754 Divide the power by 4
54 / 4 = 13 remainder 2
So 7² = 49 Unit digit 9
9 ^ 561
Power 561 is odd number
Unit digit 9
6
Answer : a
1 9 9 =
+
+
+ 25
Unit digit 5

37. 3. Find the unit digit of the product
(2012^2012)*(2013^2013)*(2014^2014)*(2015^2015)
a) 0 b) 2 c) 3 d) 5
(2012^2012) * (2013^2013) * (2014^2014) * (2015^2015)
(2^2012) * (3^2013) * (4^2014) * (5^2015)
(2^2012)
Divide the power by 4
= 12 / 4
Divisible
Unit digit is 6
(3^2013)
Divide the power by 4
= 13 / 4
Remainder 1
Unit digit is 3
(4^2014)
Power is even number
Unit digit is 6
(5^2015)
Unit digit is 5
6 6
3 5
*
*
* 0
Answer : a

38. 4. Find the unit digit of 4! + 10!
a) 0 b) 4 c) 5 d) 6
1! = 1
2! = 1 x 2 = 2
3! = 1 x 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 24
5! = 1 x 2 x 3 x 4 x 5 = 120
Next all numbers factorials Unit digit is 0
4! + 10!
4 + 0 = 4
Answer : b

39. 5. Find the unit digit of 0! + 3! + 200!
a) 0 b) 5 c) 6 d) 7
0! = 1
3! = 1 x 2 x 3 = 6
0! + 3! + 200!
1 + 6 + 0 = 7
Answer : d

40. Number of zeroes at the end
2 x 5 = 10
2 x 2 x 5 x 5 = 100
2 x 2 x 2 x 5 x 5 = 200
2 x 2 x 5 x 5 x 5 = 500
2 x 2 x 2 x 5 x 5 x 5 = 1000
So number of 2 and 5 pairs = Number of zeroes at the end

41. 1. Number of zeros at the end of
1200 + 1265000 + 1500000 + 9213000 + 2100 is
a) 2 b) 3 c) 4 d) 5
1200
1265000
1500000
9213000
2100
300
Answer : a

42. 2. Calculate the number of zeros at the end of 63!
a) 12 b) 15 c) 21 d) 14
63 ! = 1 x 2 x 3 x 4 x 5 x . . . x 63
63
5
12
5
Answer : d
= 12
= 2
14

43. 3. Calculate number of zeros at the end of 74! & 75!
a) 16 & 17 b) 16 & 18 c) 17 & 18 d) 18 & 19
74
5
14
5
= 14
2
=
16
75
5
15
5
Answer : b
= 15
3
=
18

44. 4. Calculate the number of zeros at the end of 625!
a) 155 b) 150 c) 125 d) 156
625
5
125
5
25
5
5
5
= 125
25
=
=
5
1
156
=
Answer : d

45. 5. Number of zeros at the end of (100!) X (120!)
a) 28 b) 52 c) 672 d) 252
100
5
20
5
= 20
4
=
24
120
5
24
5
= 24
4
=
28
24 + 28
= 52
Answer : b

46. 6. The number of zeros at the end of the product of all prime numbers
between 1 and 1111 is?
a) 0 b) 1 c) 225 d) 275
Only one 2 and
Only one 5
So only one zero
Answer : b

47. 7. The number of zeros at the end of the product of
74 x 75 x 76x 77 x 78 x 79 x 80 is?
a) 1 b) 2 c) 3 d) 4
5s in 75 and 80
75 = 3 x 25
= 3 x 5 x 5
80 = 16 x 5
Only 3 number of 5s
and more number of 2s
So 3 zeroes
Answer : c

48. 8. The number of zeros at the end of the product of
2 x 5 x 8 x 25 x 75 is?
a) 1 b) 2 c) 3 d) 4
5s in 5, 25 and 75
5
25 = 5 x 5
75 = 3 x 5 x 5
5 number of 5s
2
8 = 2 x 2 x 2
Only 4 number of 2s
So 4 zeros
Answer : d

49. 1. What is the highest power of 3 that can divide 100!?
100
3
33
3
11
3
3
3
= 33
1
=
48
= 11
=
3
Maximum Power

50. 2. What is the maximum power of 7 contained in 120!?
120
7
17
7
= 17
19
= 2

51. 3. What is the highest power of 4 that can divide 125!?
125
2
62
2
31
2
15
2
= 62
7
=
= 31
=
15
125! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x . . . X 125
2 x 3
4 = 2²
7
2
3
2
2^119
2² ^ ?
= 119 / 2
= 59
3
=
1
=
119

52. 4. What is the highest power of 12 that can divide 116!?
12 = 3 x 4
4 = 2²
12 = 2² x 3
116
2
58
2
29
2
14
2
= 58
7
=
= 29
=
14
7
2
3
2
2^112
2² ^ ?
= 112 / 2
= 56
3
=
1
=
112

53. 116
3
38
3
12
3
4
3
= 38
1
=
= 12
=
4
2² ^ 56 and 3^55
12 = 2² x 3
(2² x 3) ^ ?
So Maximum power of 12
= 55
55

54. 5. What is the highest power of 8 that can divide 125!?
8 = 2 x 4
= 2 x 2 x 2
= 2³
125
2
62
2
31
2
15
2
= 62
7
=
= 31
=
15
7
2
3
2
2^119
2³ ^ ?
= 119 / 3
= 39
3
=
1
=
119

55. 6. What is the maximum power of 18 in 210!?
a) 102 b) 51 c) 206 d) 103
18 = 2 x 9
= 2 x 3 x 3
= 2 x 3²
210
2
105
2
52
2
26
2
= 105
13
=
= 52
=
26
13
2
6
2
3
2
2^206
6
=
3
=
206
= 1

56. 210
3
70
3
23
3
7
3
= 70
2
=
= 23
=
7
3^102
3² ^ = ?
= 102 / 2
= 51
3² ^ 51
2 ^ 206
(2 x 3²) ^ 51
18 ^ 51
102
Answer : b