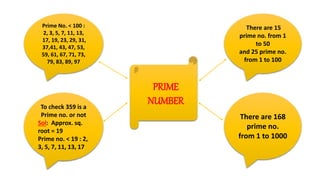
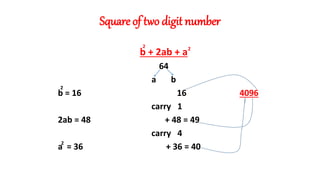
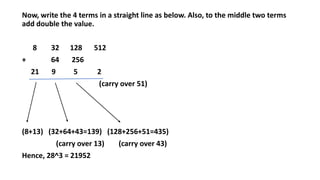
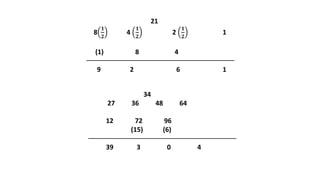
The document discusses various topics related to numbers including: 1) Perfect numbers which are numbers whose factors sum to the number. 2) Classification of numbers as natural, whole, integers, rational, and irrational. 3) Rules for divisibility including by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15. 4) Formulas for finding cubes of two-digit numbers and number of zeros in expressions.

2. B.E (final year) Computer Science Engineering, WIT Solapur.
Math is my passion
I like craft, designing and teaching.
https://unacademy.com/user/dikshiv96

3. NUMBERS
Numbers
Real Numbers Complex (Imaginary)
(a+ib) i=√-1, i²=-1,
Irrational Rational i³= -i , i4= 1
(∏, √2, √3)
Integers Fractions
Whole -ve integers
0 Natural (+ve integers)

4. • Perfect Number:
• Definition : “A perfect number is a number such that the sum of its
factors including 1 and excluding itself is equal to the number ”
Example: 1) Factors of 6 are 1,2,3
1+2+3 = 6
2)Factors of 28 are 1,2,4,7,14
1+2+4+7+14=28
• It is having a standard form 2p−1(2p−1).. Where p is prime number
• Example: perfect numbers are generated by the formula 2p−1(2p−1),
with p a prime number, as follows:
• for p = 2: 21(22−1) = 6
• for p = 3: 22(23−1) = 28
• for p = 5: 24(25−1) = 496
• for p = 7: 26(27−1) = 8128.

5. Classification of Numbers /Integers
• Natural numbers Natural numbers are counting numbers which we use to count . For
example 1,2,3…. The lowest natural number is 1
• Whole numbers When zero is included in the list of natural numbers the numbers
are known as whole numbers .for example , 0, 1, 2….the lowest whole numbers is 0 .
• Integers  Integers are whole numbers ,the negative of whole numbers and zero .for
example ,43434235 ,28,2,0,-28 and -3030 are integers, but numbers like ½ , 2.5 are not
whole numbers .
• Number line  The number line is used to represent the set of real numbers. A
representation of the number line is given below:
• Negative Integers Positive Integers

6. • Real Number:-
• Number which are present on number line are called as Real
Number. Which includes factor, decimal, zeros every possible things.
• Imaginary Number:-
• Number which are not present on number line are called as
imaginary number such number are sq. root of negative.
• e.g. √-9, √-16, √-8
• Solution of these number cannot be see on number line √-1 = I is
imaginary coefficient.
• :. √-9 is 3i, √-16 is 4i

7. • Types of Real Number:-
1) Rational Number :-
These number is present in P/Q form were both P&Q must integer & Q should not be
zero.
E.g. 3/5, -1/2, 4, 10, 3.2
2) Irrational Number:-
• Number which cannot be present in P/Q form are irrational these numbers are non
ending & non repeating.
• e.g. 2.3185….
1.6521…..

8. LCMCONCEPTS
10, 12  60
8, 12  24
14, 10  70
12, 15  60
35 50
7 10 …(Dividing by HCF 5)
70 …(LCM of small number)
70*5=350 …(Re-multiplying by HCF)
Big Number:
84 60
7 5 …(Dividing by HCF 12)
35 …(LCM of small number)
35*12=420…(Re-multiplying by HCF)
Big Number:

9. Square of two digit number
b + 2ab + a
64
a b
b = 16 16 4096
carry 1
2ab = 48 + 48 = 49
carry 4
a = 36 + 36 = 40
2
2
2 2

10. Structure form ( 31 – 80 )
N – 25 d
where,
N is the number
d is the difference between number and 50
For e.g.
1. 54 N = 54 d = 54 – 50 = 4
54 - 25 4 = 16
2. 73 N = 73 d = 73 – 50 = 23
73 – 25 = 48 23 = 529
carry = 5
2
29 16
2
2
53 29

11. STRUCTURE FORM(81 – 100 )
100 – 2d d
where,
N is the number
d is the difference between 100 and number
For e.g.
1. 88 N = 88 d = 100 – 88 = 12
100 – 2(12) = 76 12 = 144
carry 1
2 . 93 N = 93 d = 100 – 93 = 7
100 – 2(7) = 86 7 = 49
2
77 44
86 49
2
2

12. • Method to find out the cubes of two digit numbers :
• The answer has o consist of 4 parts, each of which has to be
calculated separately.
• The first part of the answer will be given by the cube of the ten’s
digit.
• Suppose you have to find the cube of 28.
• The first step is to find the cube of 2 and write it down.
• 2^3 = 8
• The next three parts of the numbers will be derived as follows.
• Derive the values 32, 128 and 512.
• (by creating a G.P. of 4 terms with the first term in this case as 8,
and a common ratio got by calculating the ratio of the unit’s digit of
the number with its tens digit. In this case the ratio is 8/2 = 4.

13. Now, write the 4 terms in a straight line as below. Also, to the middle two terms
add double the value.
8 32 128 512
+ 64 256
21 9 5 2
(carry over 51)
(8+13) (32+64+43=139) (128+256+51=435)
(carry over 13) (carry over 43)
Hence, 28^3 = 21952

14. 21
8
𝟏
𝟐
4
𝟏
𝟐
2
𝟏
𝟐
1
(1) 8 4
9 2 6 1
34
27 36 48 64
12 72 96
(15) (6)
39 3 0 4

15. For composite number
C= m x n ( Co prime )
( Rule should follow m , n )
Number of divisible /factors
If N is any number which can be factorized like
N= ap *bq *cr * ……
Where a, b, c are prime numbers.
Number of divisors = (p+1)(q+1)(r+1)…….
Q. Find the number of divisors of N =420.
N = 420 = 22 * 31 *71 * 51
So the number of divisors = (2+1)(1+1)(1+1)(1+1) = 24

16. • Number of zeroes in an expression:
• Suppose you have to find the number of zeroes in a product :
• 24*32*17*23*19=(2^3*3^1)*(2^5)*17^1*23*19.
• As you can notice, this product will have no zeroes because it has no 5 in
it.
• However, if you have an expression like : 8*15*23*17*25*22
• The above expression can be the rewritten in the standard form as;
• Zeroes are formed by a combination of 2*5. hence, the number of zeroes
will depends on the number of pairs of 2’s and 5’s that can be formed.
• In above product, there are four twos and two fives. Hence, we shall be
able to form only two pairs of (2*5).
• Hence, there will be 2 zeroes in the product.

17. Process for finding the number of zeroes :
Q. 81!
81/5 = 16
16/5 = 3
Thus, Answer = 16+3 = 19
Q. Find the number of zeroes in 27!
Number of zeroes is 27! = (27/5) + (27/25) where [x] indicates the integer
just lower than the fraction.
Hence, [27/5] = 5 and [27/5^2] = 1+6 = 7 zeroes.
Q. Find the number of zeroes in 137!
[137/5] + [137/5^2] + [137/5^3]
= 27+5+1 = 33 zeroes.

18. • Q. What power of 8 exactly divides 25! ?
• Sol. If were a prime number, the answer should be [25/8] = 3. But since 8
is not prime, use the following process.
• The prime factors of 8 is 2*2*2. For divisibility by 8, we need three twos.
So, every time we can find 3 twos, we add one to the power of 8 that
divides 25! To count how we get 3 twos, we do the following. All even
numbers will give one ‘two’ at least [25/2] = 12.
• Also, all numbers in 25! Divisible by 2^2 will give an additional two
[25/2^2] = 6
• Further, all number in 25! Divisible by 2^3 will give a third two. Hence
[25!/2^3] = 3
• And all numbers of twos in 25! Divisible by 2^4 will give a fourth two.
Hence [25!/2^4] = 1
• Hence, total number of twos in 25! Is 22. For a number to be divided by 8,
we need three twos. Hence, since 25! has 22 twos, it will be divided by 8
seven times.

19. PRIME
NUMBER
Prime No. < 100 :
2, 3, 5, 7, 11, 13,
17, 19, 23, 29, 31,
37,41, 43, 47, 53,
59, 61, 67, 71, 73,
79, 83, 89, 97
To check 359 is a
Prime no. or not
Sol: Approx. sq.
root = 19
Prime no. < 19 : 2,
3, 5, 7, 11, 13, 17
There are 15
prime no. from 1
to 50
and 25 prime no.
from 1 to 100
There are 168
prime no.
from 1 to 1000

20. • Divisibility Rules 
• For 2 : If unit digit of any number is 0,2,4,6 or 8, then that number will be divisible by 2
• For 3 : If sum total of all the digits of any numbers is the visible by 3 then the number will be
divisible by 3, (e g ; 123 ,456 etc )
• For 4 : If the last two digits of a numbers are divisible by 4 , then that number will be divisible
by 4 (e g ; 3796 ,248 etc )
• For 5 : If the last digit of the number is 5 or 0 , then that number will be divisible by 5
• For 6 : Rule should follow 2 , 3
• For 7 : ( R -2L) should be multiple of 7
• R  Remaining number
• L  Last digit
• e g :- 441 , here R = 44 & L = 1 hence ,
• R- 2L= 44 – 2(1)
• =42

21. • For 8  If the last 3 digits of the number are divisible by 8, then the number itself will
be divisible by 8 .
• E g ;128, 34568 etc
• For 9  If the sum of the digit of the numbers is divisible by 9 .
• E g; 129835782
• For 11  The difference between the sum of the digit at the even places and the sum
of the digits at the odd places is divisible by 11/0
• e g ; 6595149 is divisible by 11
• 6+9+1+9 (odd) = 25 and
• 5+5+4 (even) = 14
• For 12  divisible by 3 & 4
• For 13  (R + 4L)
• e g ; 1404
• R = 140 L= 4
• 140 +16 = 156 (13n)
• For 14  both by 2 & 7
• For 15  by 5 & 3