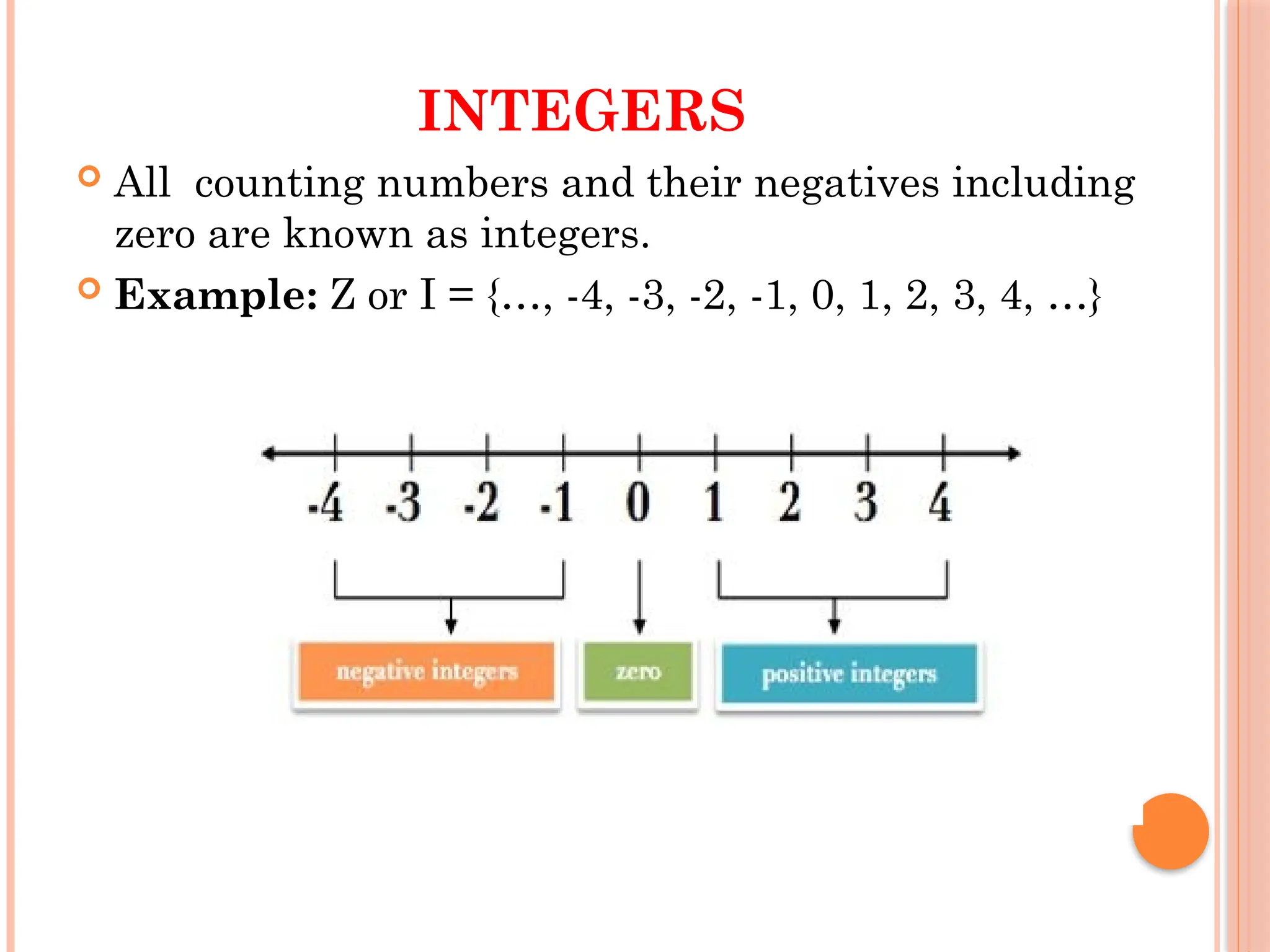
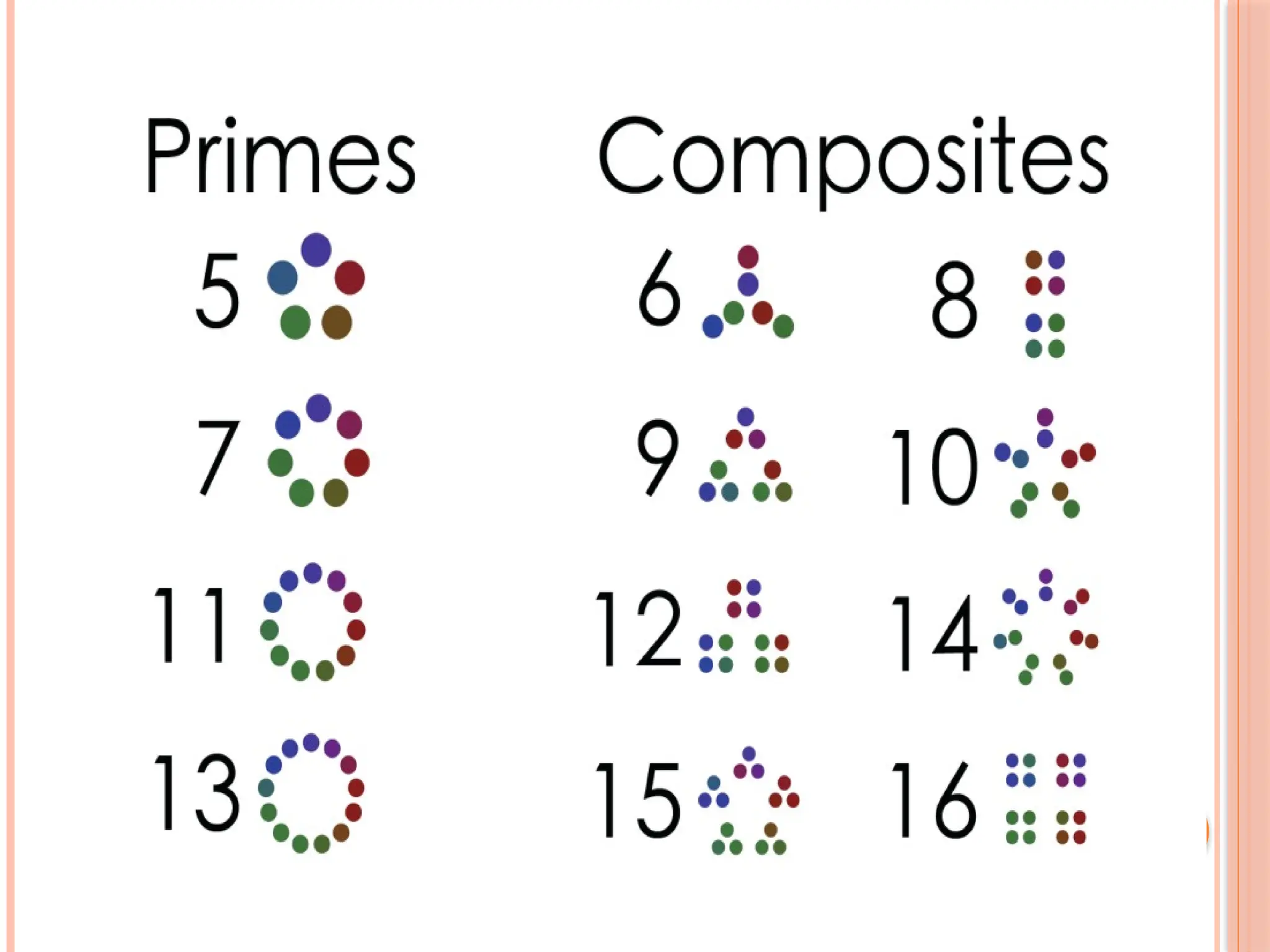
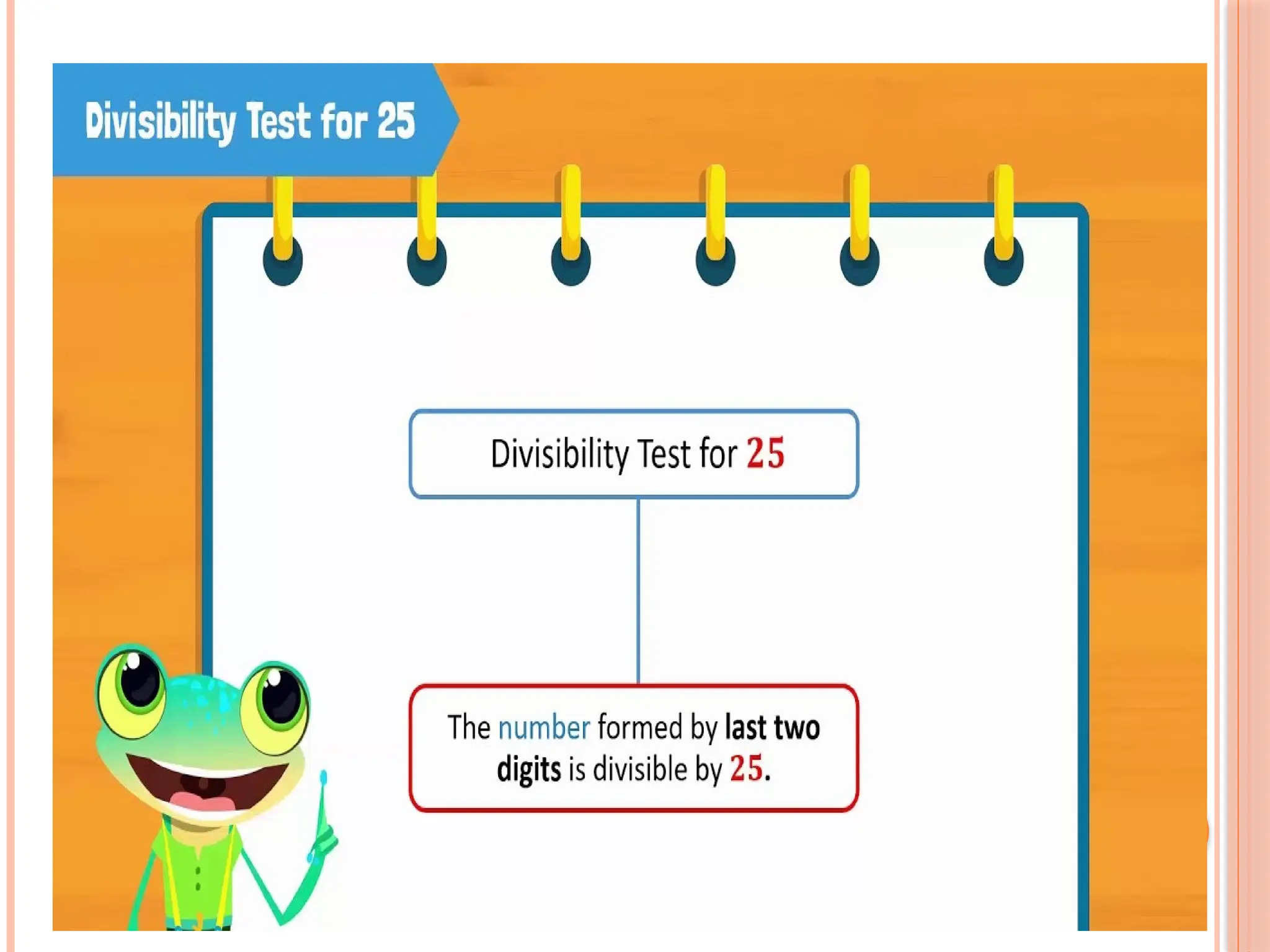
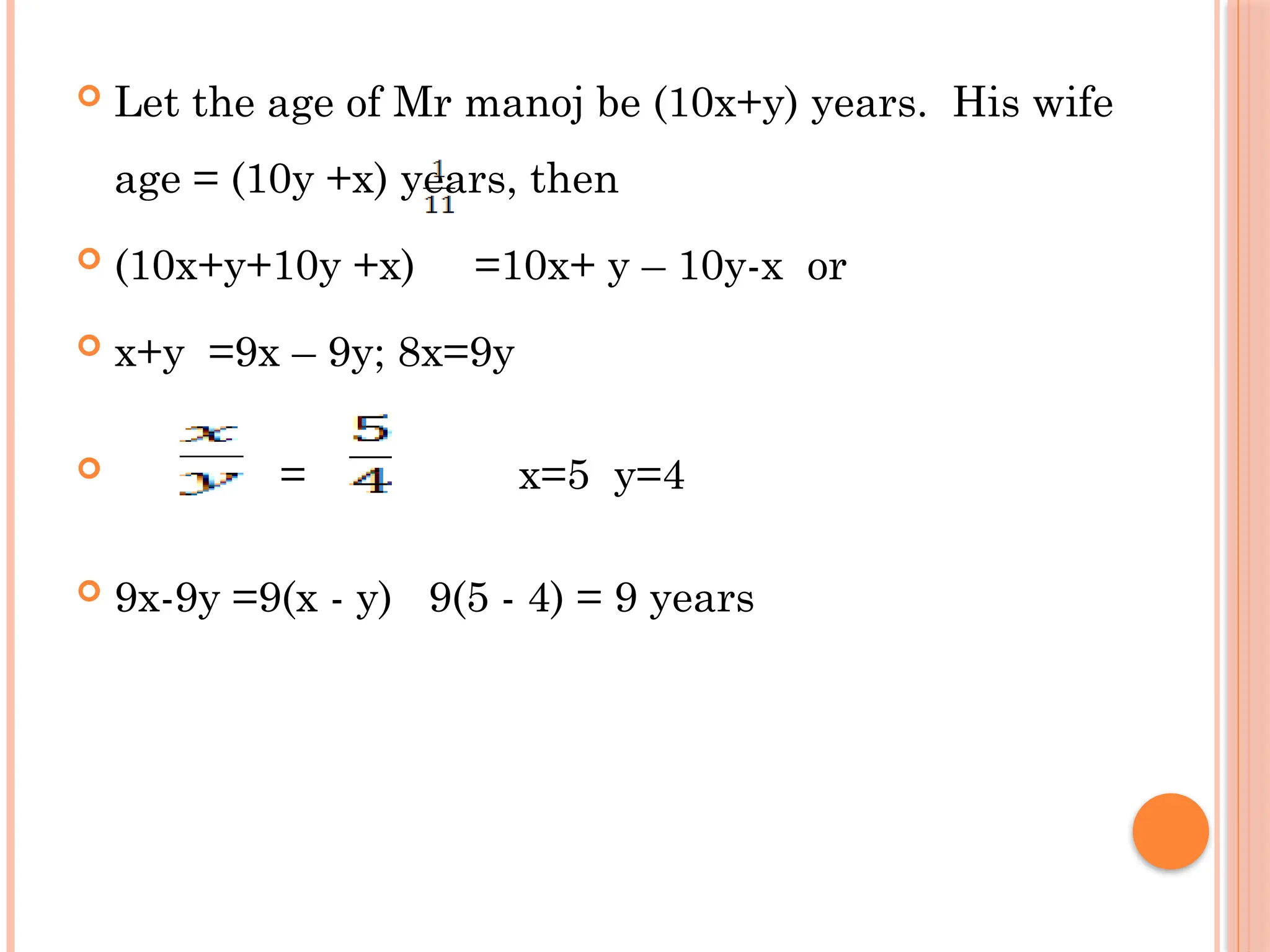The document outlines various mathematical concepts, including types of numbers such as natural numbers, whole numbers, integers, rational numbers, and irrational numbers. It provides definitions, examples, and methods for arithmetic operations including addition, subtraction, and multiplication, along with rules for divisibility. Additionally, it discusses prime numbers and composite numbers, and presents problem-solving techniques related to remainders and divisibility tests.

1. Presented By
Mrs. K.SASIKALA,
Assistant Professor,
DEPT. OF MATHEMATICS
MOOKAMBIGAI COLLEGE OF ENGINEERING
MOOKAMBIGAI COLLEGE OF ENGINEERING
DEPARTMENT OF MATHEMATICS

2. NUMBERS
 A number is a mathematical object used to count,
measure and label.
 The examples are 0, 1, 2, 3, 4, and so on.

3. NATURAL NUMBERS
 Counting numbers 1, 2, 3, 4, 5, … are known as
natural numbers
 Example : N = {1, 2, 3, 4, 5,…}

4. WHOLE NUMBERS
 If we include 0 among the natural numbers, then
the numbers 0, 1, 2, 3, 4, 5, ... are called whole
numbers.
 Example : W={0, 1, 2, 3, 4, 5, …}

5. POSITION OF NUMBERS

7. TEN
CRORE
10
8
CRORE
10
7
TEN
LAKHS
10
6
LAKHS
10
5
TEN
THOUSAND
10
4
THOUSAND
10
3
HUNDRED
10
2
TEN
10
UNITS
10
0
3 0 9 8 7 2 5 4 6

8.  10 = 1 ZERO – 101
 100=2 ZEROS – 102
 1000=3 ZEROS – 103
 MILLION =1,000,000 – 106
 BILLION = 1,000,000,000 – 109
 TRILLION = 1,000,000,000,000,000 – 1012
 QUADTRILLION = 1015
 1 MILLION = 10 LAKHS
 10 MILLION = 1 CRORE
 1 BILLION = 100 CRORE
 1 TRILLION = 1 LAKH CRORE

9. INTEGERS
 All counting numbers and their negatives including
zero are known as integers.
 Example: Z or I = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

10. POSITIVE INTEGERS
 The set I+
={1, 2, 3, 4, …} is the set of all positive
integers starts from 1 is called positive integer.

11. NEGATIVE INTEGERS
 The set I-
={-1, -2, -3, -4, …} is the set of all
negative integers.
 0 is belongs to neither positive nor negative.

12. NON- NEGATIVE INTEGERS
 The set {0, 1, 2, 3, 4, 5, …} is the set of non-
negative integers.

13. RATIONAL NUMBERS
 The numbers of the form where p and q are
integers.
 Example:
 The set of all rational numbers is denoted by Q.
,
1
0
,
8
5
,
2
3
,
7
4


16. IRRATIONAL NUMBERS
 Those numbers which expressed in decimal form
are neither terminating nor repeating decimals
are known as irrational numbers.

17. REAL NUMBERS
 The rational and irrational numbers combined
together to form real numbers.
 Example:

18. EVEN NUMBERS
 All those numbers which are exactly divisible by 2
are called even numbers.
 Example: 2, 6, 8, 10, etc

19. ODD NUMBERS
 All those numbers which are not exactly divisible by
2 are called odd numbers.
 Example: 1, 3, 5, 7, etc

20. PRIME NUMBERS
 A natural number other than 1, is a prime
number if it is divisible by 1 and itself only.
 Example: 2, 3, 5, 7, etc

21. COMPOSITE NUMBERS
 Natural numbers greater 1 which are not prime
numbers are composite numbers
 Example: 4, 6, 9, 15 etc.

23. CO – PRIME NUMBERS
 Two numbers which have only 1 as the common
factors are called co- prime numbers or
relatively prime to each other.
 Example: (3, 7), (8, 9), (36, 25) etc.

24. ADDITION AND SUBTRACTION
 54321-(9876+8967+7689) = ?
5 4 3 2 1
9 8 7 6
8 9 6 7
7 6 8 9
--------------
2 7 7 8 9
--------------
First step
 Add first column 6+7+9 =22
 To obtain 1 at unit place add 9 to make 31
 In the answer write 9 at unit’s place and carryover
3

25.  Step 2
Add 2nd
column 3+7+6+8 =24
To obtain 2 at ten’s place, add 8 to make 32
In the answer, write 8 at ten’s place and carry over 3.
 Step 3
Add 3rd
column 3+8+9+6 =26
To obtain 3 at hundred’s place, add 7 to make 33.
In the answer, Write 7 at hundred’s place and carry over 3
 Step 4
Add 4th
column 3+9+8+7 = 27
To obtain 4 at thousand’s place, add 7 at thousand’s place and
carry over 3
 Step 5 5th
column
To obtain 5 at ten thousand’s place add 2 to it to make 5.
In the answer, write 2 at the ten thousand’s place.
 54321-(9876+8967+7689) = 27789

26. MULTIPLICATION
 Multiplication of a given number by 9,99,999 etc
that is by 10n
-1
 Method
Put as many zeros to the right of the
multiplicant as there are nines in the
multiplier and from the result subtract
the multiplicant and get the answer.

27.  Multiply 3893 by 99
3893×99 =389300 – 3893 = 385407
 Multiply 4327 by 999
4327 × 999 = 4327000 – 4327 = 4322673
 Multiply 5863 by 9999
5863 × 9999 = 58630000 – 5863 = 58624137

28.  Multiplication of a given number by 11,
101,1001 etc that is by 10n
-1
 Method
Place n zeros to the right of the
multiplicand and then add the
multiplicant to the number so
obtained.

29.  Multiply 4782 × 11
4782 × 11 = 47820 +4782 = 52602
 Multiply 9836 × 101
9836 × 101 = 983600 + 9836 = 993436
 Multiply 6538 × 1001
6538 × 1001 = 6538000 + 6538 = 6544538

30.  Multiplication of a given number by 15, 25,35 etc
that is by 10n
-1
 Method
 Double the multiplier and then multiply the
multiplicant by this new number and
finally divide the product by 2

31.  Multiply 7054 × 15
7054 × 15 =
= = 105810
 Multiply 3897 × 25
3897 × 25 =
= = 97425
 Multiply 4536 × 35
4536 × 35 =
= = 159705

32. DIVISIBLE BY 2
 A number is divisible by 2 if the unit’s digit is
zero or divisible by 2
 Example: 4, 12, 18, 30, 102, etc

33. DIVISIBLE BY 3
 A number is divisible by 3 if the sum of digits in the
number is divisible by 3.
 Example: 3792 is divisible by 3
since 3+7+9+2 = 27 which is divisible by 3

34.  A number is divisible by 4 if the number formed
by last two digits ( ten’s digit and unit’s digit ) is
divisible by 4 or are both zero.
DIVISIBLE BY 4

35. DIVISIBLE BY 5
 A number is divisible by 5 if the unit’s digit in
the number is 0 or 5.
 For example 13520, 7805,640,745

36. DIVISIBLE BY 6
 A number is divisible by 5 if the is even and sum
of its digits is divisible by 3.
 Example : 4518 is divisible by 6 since it is even
and sum of its digits 4+5+1+8 = 18 is divisible by
3

37. DIVISIBLE BY 7
 The unit digit of the given number is doubled and
then it is subtracted from the number obtained
after omitting the unit digit.
 If the number is divisible by 7 , then the given
number is also divisible by 7
 For example : 448, on doubling the unit digit 8 of
448 we get 44 then 44-16 = 28
 Since 28 is divisible by seven, the 448 is divisible
by 7

39. DIVISIBLE BY 8
 A number is divisible by 8 if the number formed by
the last 3 digits is divisible by 8.
 For example the number 41784 is divisible by 8 as the
number formed by last 3 digits 784 is divisible by 8

40. DIVISIBLE BY 9
 A number is divisible by 9 if the sum of its digits
is divisible by 9
 For example the number 19044 is divisible is
divisible by 9 as the sum of its digits 1+9+0+4+4
= 18 is divisible by 9

41. DIVISIBLE BY 10
 A number is divisible by 10 if it ends in zero.
 For example the last digit of 580 is zero. Therefore
580 is divisible by 10.

42. DIVISIBLE BY 11
 A number is divisible by 11 if the difference of the
sum of the digits at odd places and sum of the digits
at even places is either zero or divisible by 11
 For example in the number 38797, the sum of the
digits at odd places is 3+7+7 = 17 and sum of the
digits at even places is 8+9 = 17.
 The difference is 17-17=0 .
 So the number is divisible by 11

44. DIVISIBLE BY 12
 A number is divisible by 12 if it is divisible by 3
and 4

45. DIVISIBLE BY 18
 An even number satisfying the divisibility test of
9 is divisible by 18

46. DIVISIBLE BY 25
 A number is divisible by 25 if the number formed
by the last two digits is divisible by 25 or the last
two digits are zero.
 For example the number 13675 is divisible by 25 as
the number formed by last two digits is divisible by
25 or the last two digits is 75 which is divisible by
25.

48.  DIVISIBLE BY 88
 A number is divisible
by 88 if it is divisible
by 11 and 8.
Divisible by 125
 A number is divisible by 125
if the number formed by last
three digits is divisible by 125
or last three digits are zero.
 The number 5250is divisible
by 125 as 250 is divisible by
125

49. SOME USEFUL SHORT-CUT METHODS
 Test to find whether a given number is a prime.
 Step 1
 Select a least positive integer n such that n2
> given
number
 Step 2
 Test the divisibility of given number by every prime
number less than n.
 Step 3
 The given number is prime only if it is not divisible by
any of these primes.

50.  Investigate, whether 571 is a prime number
 Since (23)2
= 529 < 571 and (24)2
= 576 > 571
 So n=24
 Prime numbers less than 24 are 2,3,5,7,11,13,17,19,23 and
24 is divisible by 2, 571 is not prime number.
 Investigate, whether 923 is a prime number.
 Since (30)2
= 900 < 923 and (31)2
= 961 >923
 So n=31
 Prime numbers less than 31 are 2,3,5,7,11,13,17,19,23, 29.
since 923 is not divisible any of these primes. Therefore
923 is a prime number.

51.  The least number, which when divided by d1, d2
and d3 leaves the reminders r1,r2 and r3
respectively such that (d1 -r1)= (d2 –r2) = (d3 –r3) is
(LCM of d1, d2 and d3) - (d1 -r1) or (d2 –r2) or (d3 –r3).

52.  Find the least number which when divided by 9,
10 and 15 leaves the reminders 4, 5 and 10
respectively.
 Here 9-4 = 10-5 =15-10 = 5
 Also LCM (9,10,15) =90
 The required least number is 90-5 = 85.

53.  The number on being divided by d1 and d2
successively leaves the reminders r1 and r2
respectively. If the number is divided by d1 × d2
then reminder is = (d1 × r2 + r1 ).
 A number on being divided by 10 and 11
successively leaves the reminders 5 and 7
respectively. Find the remainder when the same
number is divided by 110.
 The required remainder is d1 × r2 + r1 = 10 × 7+5
= 75

54.  To find the number of numbers divisible by a
certain integer.
 How many numbers up to 532 are divisible by
15?
 We divide 532 by 15 = 35.7
 532= 35 × 15 +7
 The quotient obtained is the required number of
numbers. Thus, there are 35 such numbers

55.  How many numbers up to 300 are divisible by 5
and 7 together?
 The LCM of 5 and 7 = 35
 We divide 300 by 35
 300 = 8 × 35 +20
 Thus there are 8 such numbers.

56.  Two numbers when divided by a certain
divisor give remainders r1 and r2. When
their sum is divided by the same divisor, the
remainder is r3. the divisor is given by r1 + r2
- r3.

57.  Two numbers when divided by a certain
divisor give remainders 473 and 298. When
their sum is divided by the same divisor, the
remainder is 236. Find the divisor.
 The divisor is given by r1 + r2 - r3.
 473+298 -236 = 499

58.  Problem 1
 9999+ 8888+777 + ? = 19700
(a) 36 (b) 16
(c) 64 (d) 26
The answer is (a) 36
Let 9999+ 8888+777 + x = 19700
X= 19700 -19664 =36

59.  Problem 2
 If the two digits of the age of Mr. Manoj are reversed
then the new age so obtained is the age of his wife.
of the sum of their ages is equal to the difference
between their ages. If Mr. manoj is older than his wife
then find the difference between their ages.
(a) Cannot be determined
(b) 8 years
(c) 9 years
(d) 7 years
The answer is (c) 9 years

60.  Let the age of Mr manoj be (10x+y) years. His wife
age = (10y +x) years, then
 (10x+y+10y +x) =10x+ y – 10y-x or
 x+y =9x – 9y; 8x=9y
 = x=5 y=4
 9x-9y =9(x - y) 9(5 - 4) = 9 years

61.  Problem 3
 In a division sum, the divisor is 12 times the quotient
and 5 times the reminder. If the remainder be 48,
then the dividend is
 (a) 240 (b) 576
 (c) 4800 (d) 4848
 The answer is (d) 4848
 Let the quotient =Q and remainder = R then the
given is 12Q = 5R, R = 48, 12Q = 5×48, Q = 20,
dividend = 20 × 240 + 48 =4848

62.  Problem 4
 What least number must be subtracted from
1294 so that the remainder when dividend by 9,
11, 13, will leave in each case the same
remainder 6?
 (a) 0 (b) 1
 (c) 2 (d) 3
 The answer is (b) 1
The number when divided by 9 , 11 and 13
leaving remainder 6 = (LCM of 9, 11, 13) +6 = 1293
So required number is 1294 -1293 =1

63.  Problem 5
 Three numbers are in the ratio 3:4:5, the sum of
the largest and the smallest equals the sum of
the third and 52. the smallest number is :
 (a) 20 (b) 27
 (c) 39 (d) 52
 The answer is (c) 39
 Let the numbers be 3x, 4x and 5x
 Then 5x+ 3x =4x + 52, 4x = 52 , x = 13,
 The smallest number is 3x = 3 × 13 = 39

64.  Problem 6
 The sum of three numbers is 68. if the ratio
between first and second is 2:3 and that between
second and third is 5:3, then the second number
is
 (a) 30 (b) 20
 (c) 58 (d) 48
 The answer is (a) 30
 Let the number a,b,c
 Then
 So a:b: c 10: 15 : 9 let the numbers be 10x, 15x, 9x
 Then 10x+15x+9x = 68 , 34x = 68, x= 2
 The second number is 15x = 15× 2 = 30

65.  Problem 7
 What is the sum of all prime numbers from 60 to
80?
 (a) 361 (b) 341
 (c) 351 (d) 349
 The answer is (c) 351
 61+67+71+73+79 = 351

66.  Problem 8
 Which one of the following is the largest prime
number of three digits?
 (a) 997 (b) 999
 (c) 991 (d) 993
 The answer is (a) 997
 Problem 9
 The nearest figure to 58701 which is divisible
by 567 is
 (a) 58968 (b) 58434
 (c) 58401 (d) none of these
 The answer is (a) 58968
 On dividing 58701 by 567
 Remainder = 300> ½(567), 58701 +(567-300)
 58701+267 = 58968

67.  Problem 10
 The nearest whole number to one million which is
divisible by 537 is
 (a) 1000106 (b) 999894
 (c) 1000437 (d) 999563
 The answer is (b) 999894
 On dividing 100000 by 537 , remainder 106 < 537/2,
 The nearest whole number to one million which is
divisible by 537 = 100000 -106 = 999894

68.  Problem 11
 The sum of squares of two numbers is 80 and the
square of their difference is 36. the product of
the two numbers is;
 (a) 22 (b) 44
 (c) 58 (d) 116
 The answer is (a) 22
 Let the numbers be a and b
 2ab = 80 -36 = 44
 ab = 22

69.  Problem 12
 Two numbers when divided by a certain divisor give
remainders 43 and 37 respectively. When their sum is
divided by the same divisor, the remainder is 13 . Find
the divisor.
 (a) 71 (b) 67
 (c) 57 (d) 77
 The answer is (b) 67
 The divisor = 43 + 37 =80 -13 =67

70.  Problem 13
 For what value of K, the number 7236K2 is
divisible by 8?
 (a) 7 (b) 5
 (c) 4 (d) 9
 The answer is (a) 7
 The last three digits 6K2 is divisible by 8 if k is 3
or 7 since 632 and 672 are divisible by 8
 So the answer is 7

71.  Problem 13
 The difference between a two digit number and the
number obtained by interchanging the two digits of
the numbers is 36. what is the difference between the
two digits of the number?
 (a) 6 (b) 4
 (c) 3 (d) cannot be determined
 (e) none of these.
 The answer is (b) 4
 Suppose the two digit number = 10x+y then
 (10x+y-10y-x ) = 36
 9(x-y) =36
 x-y =4

72.  Problem 14
 A 4 - digit number is formed by repeating a 2-
digit number such as 2525, 3232 etc. any number
of this form is always exactly divisible by
 (a) 7 (b) 11
 (c) 13 (d) smallest 3-digit prime
number.
 The answer is (d) smallest 3-digit prime number.
 101is the smallest 3-digit prime number

73.  Problem 15
 When a number is divided by 31 , the remainder is 29.
When a same number is divided by 16, what will be
the remainder?
 (a) Data inadequate (b) 13
 (c) 15 (d) 11 (e) None of these.
 The answer is (a) Data inadequate
 The quotient is not given. Hence remainder canot be
determined.

74.  Problem 16
 While solving mathematical problem, samidha
squared a given number and then subtracted 25
from it rather than doing what was required. i.e
first subtracting 25 from the number and then
squaring it. But she got the right answer. What
was the given number?
 (a) 48 (b) 13
 (c) 38 (d)Cannot be determined.
 (e) None of these.
 The answer is (b) 13
 Suppose the number is x, then x2 -25 =(x-25)2
 x2
-25 =x2
-50x+625; 50x= 650
 X=13

75.  Problem 17
 Two fifths of one- third of three – seventh of a number
is 15. what is the 40% of that number?
 (a) 136 (b) 140
 (c) 72 (d) none of these
 The Answer is (d) None of these
 Let the number be x then

