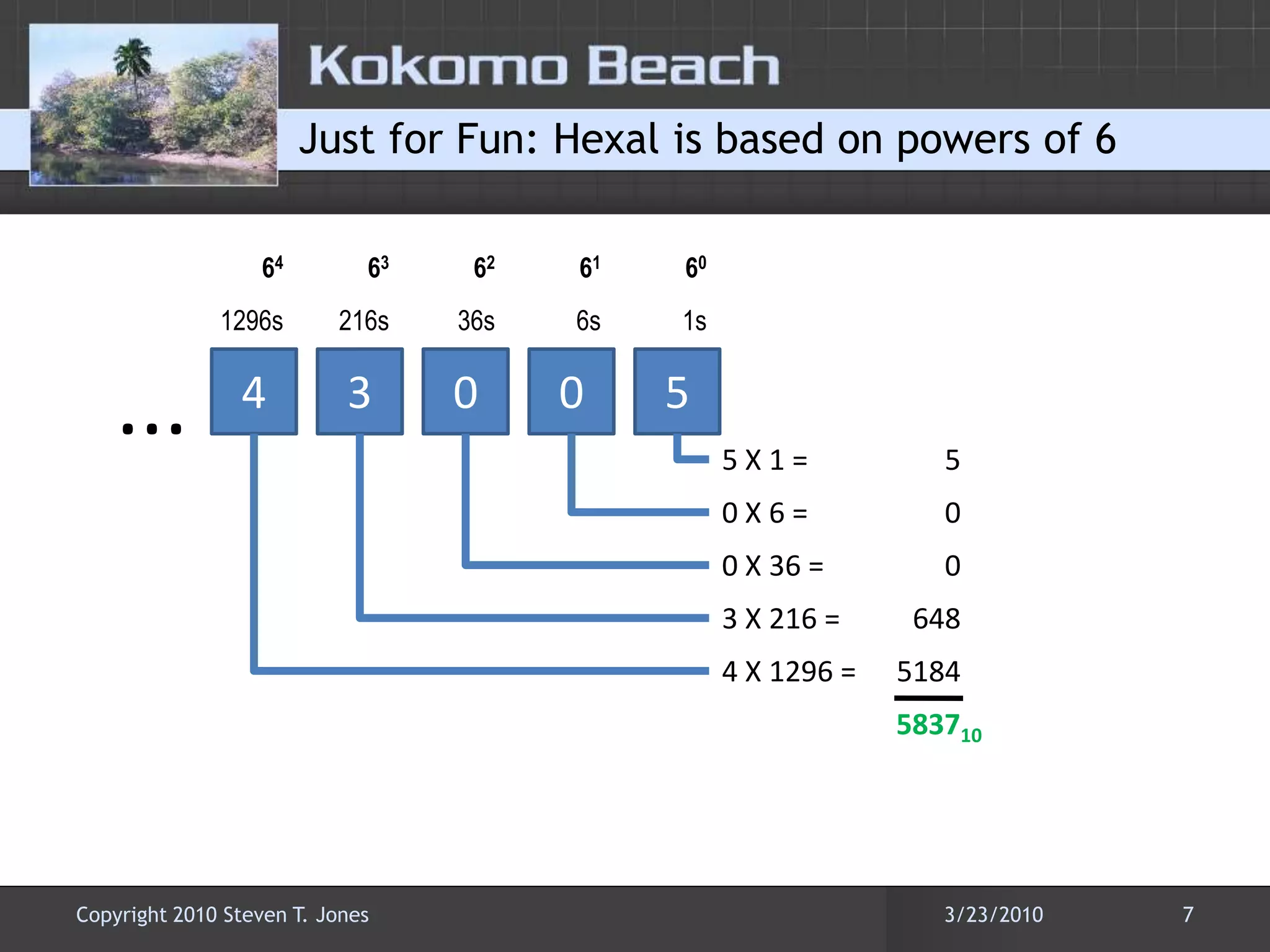
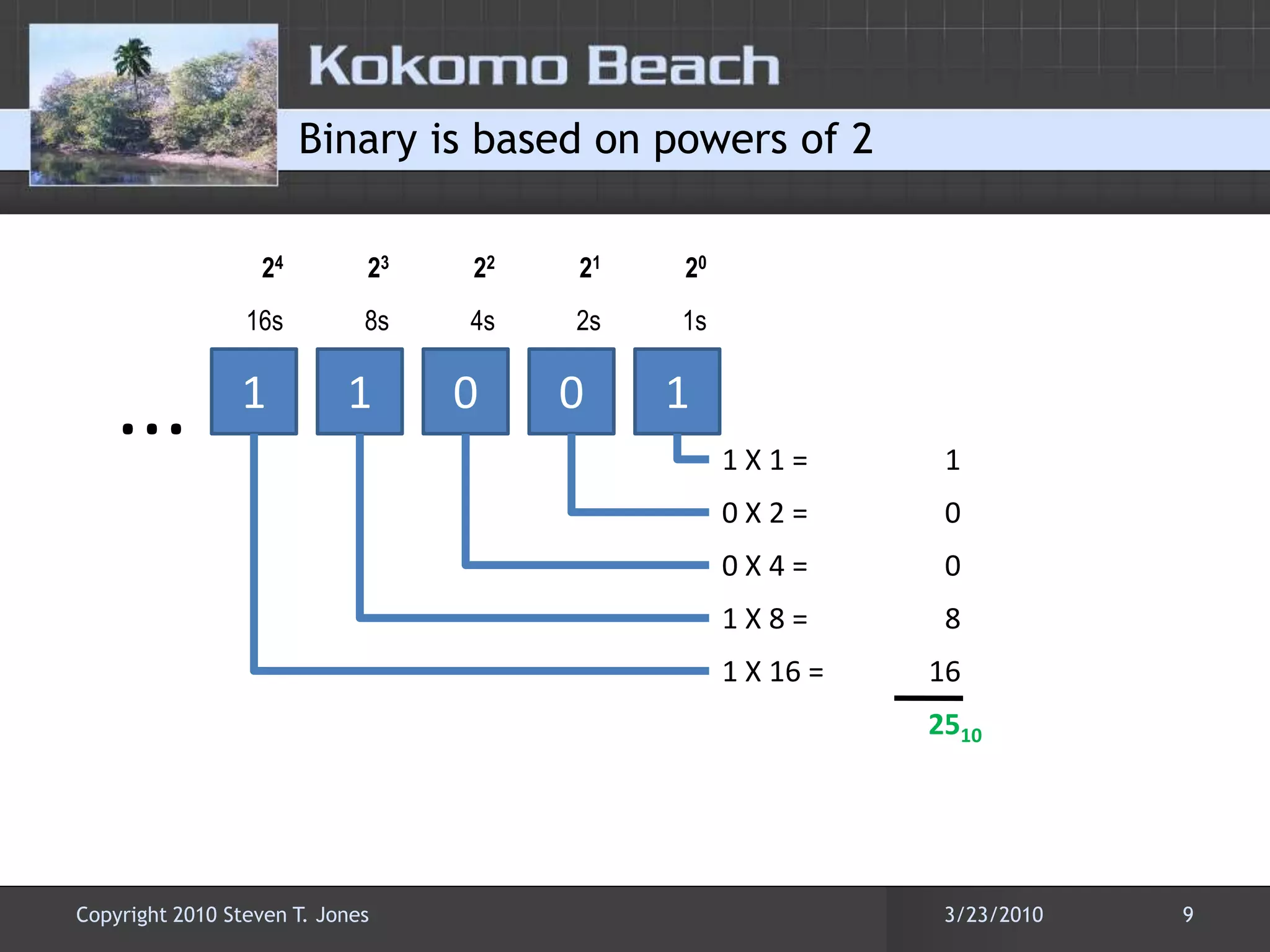
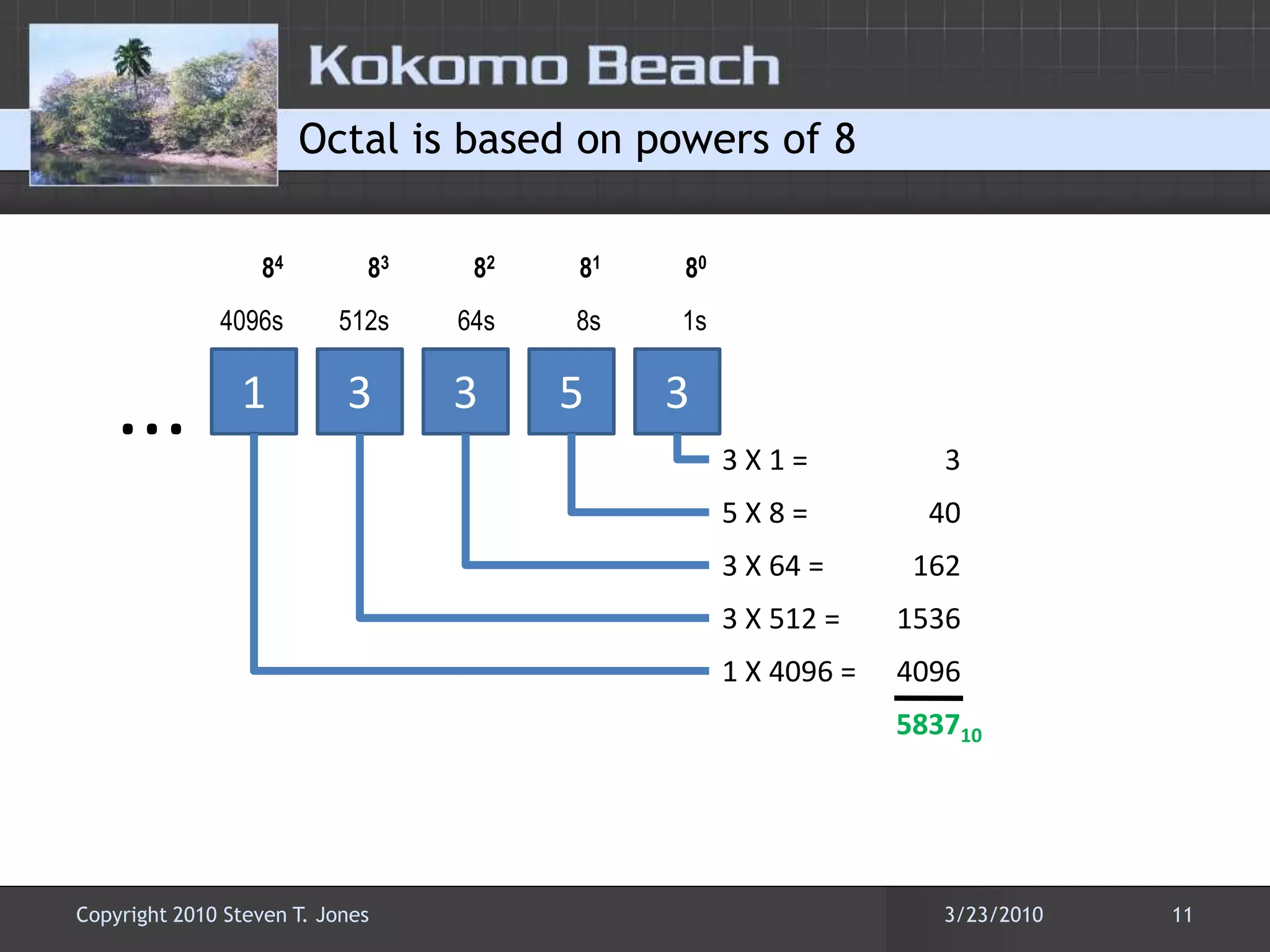
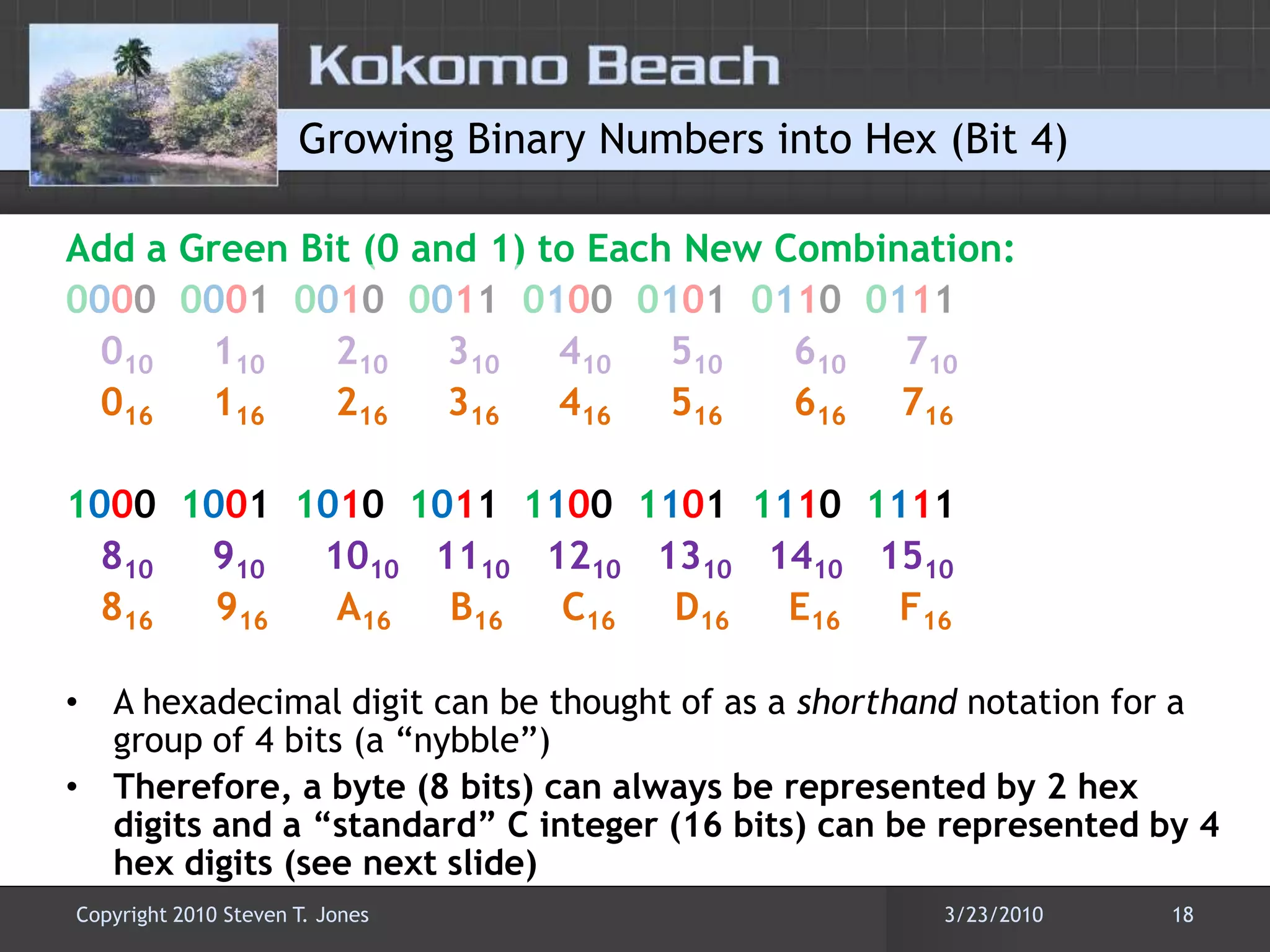
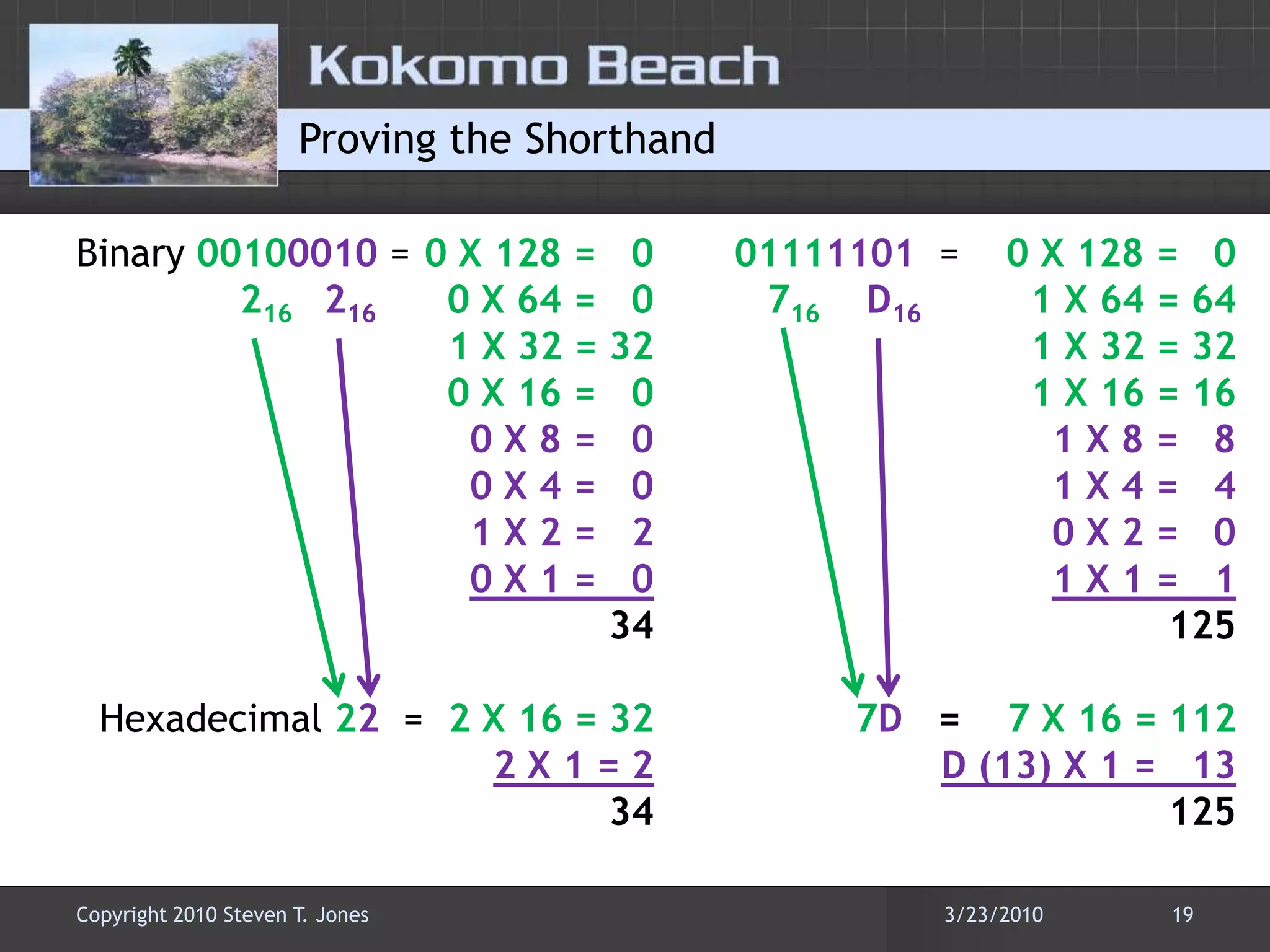
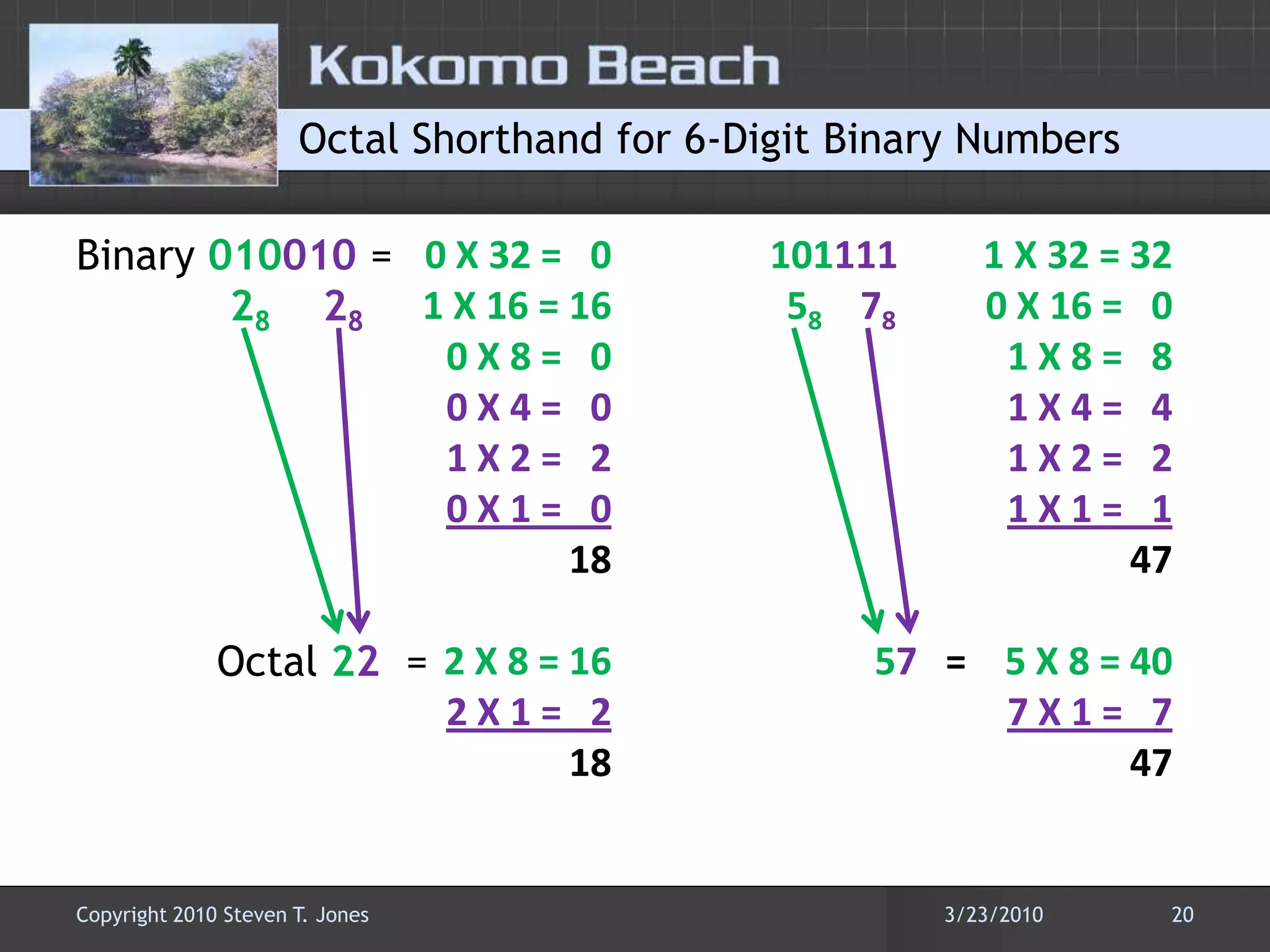
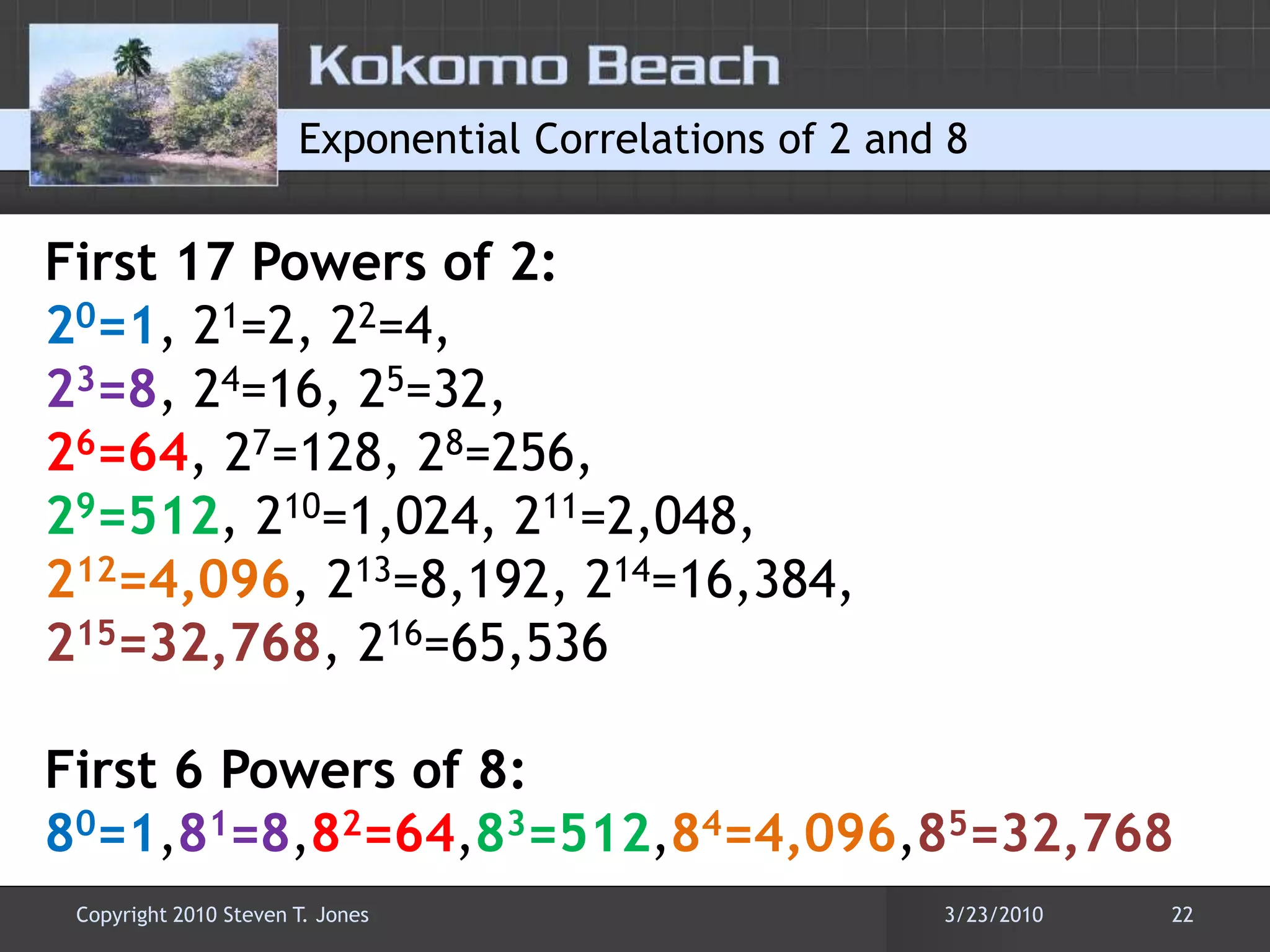
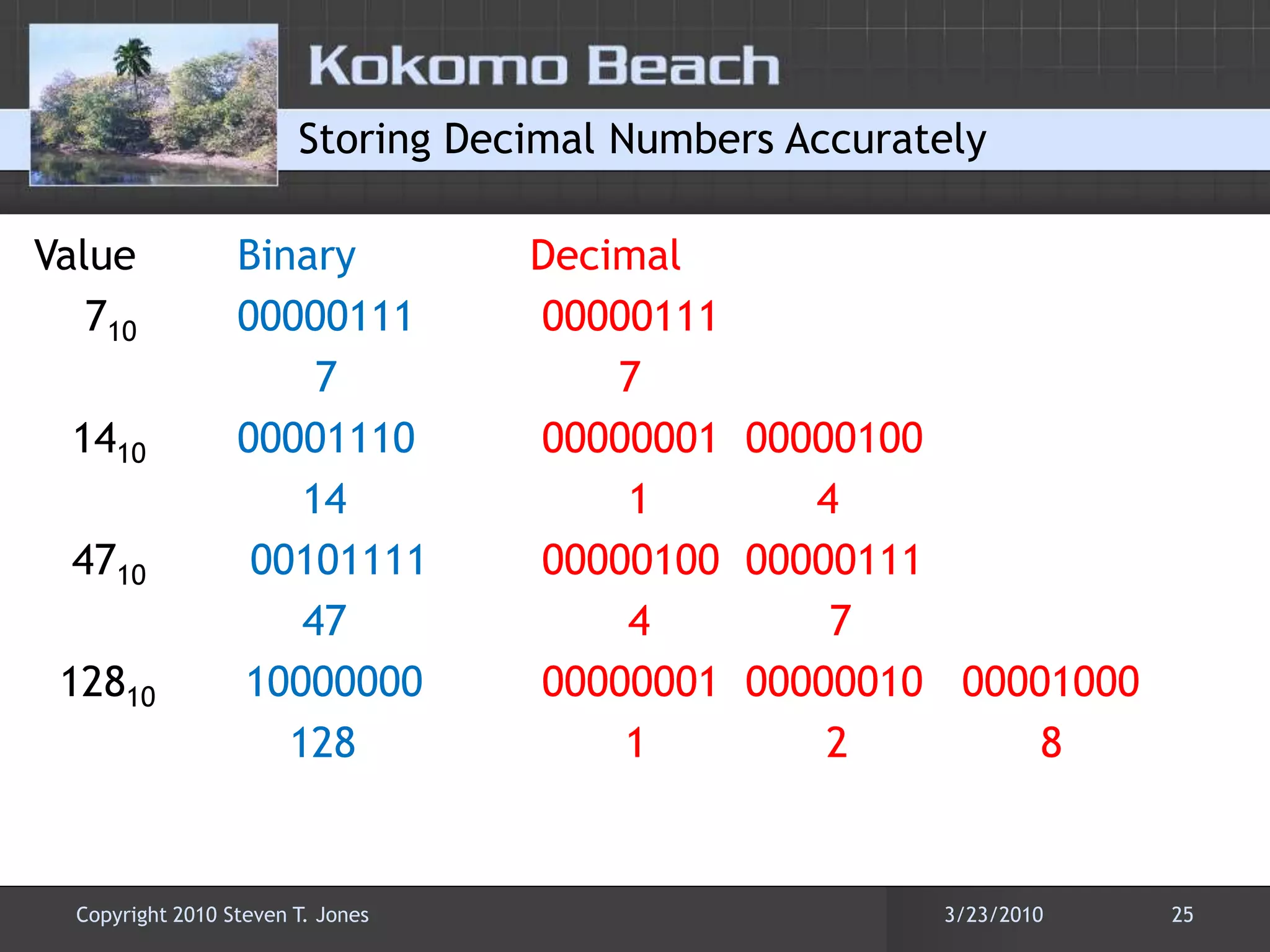
This document discusses number base conversions and the rules for different number bases. It begins by explaining that number bases correspond to the number of available digits, with digits representing powers of the base. It then provides examples of counting in binary, octal, decimal, and hexadecimal. The document demonstrates how to convert numbers between these bases by determining the place value of each digit. It also explains how shorthand notations like hexadecimal are possible due to exponential correlations between powers of 2, 8, and 16.

1. Number Base ConversionsSteven T. Jones3/22/20101Copyright 2010 Steven T. Jones

2. General RulesThe number base corresponds to the number of digits availableDigits are positional, with each position representing a power of the base (more later)Base 10 (decimal) has ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)Base 2 (binary) has two digits (0, 1)Base 8 (octal) has eight digits (0, 1, 2, 3, 4, 5, 6, 7)Base 6 (hexal – included only as an example) has six digits (0, 1, 2, 3, 4, 5)

3. General RulesBase 16 (hexadecimal) has sixteen digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)Note that the “letters” are actually digits in base 16A16 = 1010, B16 = 1110 ... F16 = 1510Why those particular “letters”? Because people familiar with the English alphabet understand that “A” comes before “B”, i.e. “A” < “B”

4. General RulesAll number bases begin with 0The largest digit in each base is one less than the baseThe largest digit in base 10 is 9The largest digit in base 2 is 17 in base 8; F (=1510) in base 16; 5 in base 6This means the base number is always represented by the digits “1” and “0”: 10102 = 210; 108 = 810; 1016 = 1610; 106 = 610See examples of counting, next slide

5. The significance of “10”Counting in base 20 (= 010)0 + 1 = 1 (= 110) 1 + 1 = 10 (= 210)Counting in base 80 (= 010)0 + 1 = 1 (= 110)1 + 1 = 2 (= 210)2 + 1 = 3 (= 310)3 + 1 = 4 (= 410)4 + 1 = 5 (= 510)5 + 1 = 6 (= 610)6 + 1 = 7 (= 710)7 + 1 = 10 (= 810)Counting in base 1000 + 1 =11 + 1 = 22 + 1 = 33 + 1 = 44 + 1 = 55 + 1 = 66 + 1 = 77 + 1 = 88 + 1 = 99 + 1 = 10

6. Decimal is based on powers of 101031021011001041000s100s10s1s10000s...58377 X 1 = 73 X 10 = 308 X 100 = 8005 X 1000 = 50000 X 10000 = 0583710(duh)3/22/20106Copyright 2010 Steven T. Jones

7. Just for Fun: Hexal is based on powers of 66362616064216s36s6s1s1296s...300545 X 1 = 50 X 6 = 00 X 36 = 03 X 216 = 6484 X 1296 = 51845837103/22/20107Copyright 2010 Steven T. Jones

8. Converting 583710 to HexalThe first six powers of 6:60 = 1, 61 = 6, 62 = 36, 63 = 216, 64 = 1296, 65=77761. How many 7776s are there in 5837? none2. How many 1296s are there in 5837? 41296 * 4 = 5184, 5837 - 5184 = 653 remaining 3. How many 216s are there in 653? 3216 * 3 = 648, 653 - 648 = 5 remaining 4. How many 36s are there in 5? 05. How many 6s are there in 5? 06. Leaving 51s 5 583710 = 43,00563/22/20108Copyright 2010 Steven T. Jones

9. Binary is based on powers of 223222120248s4s2s1s16s...100111 X 1 = 10 X 2 = 00 X 4 = 01 X 8 = 81 X 16 = 1625103/22/20109Copyright 2010 Steven T. Jones

10. Converting 2510 to BinaryThe first six powers of 2:20= 1, 21= 2, 22= 4, 23= 8, 24= 16, 25=321. How many 32s are there in 25? none2. How many 16s are there in 25? 116 * 1 = 16, 25 - 16 = 9 remaining 3. How many 8s are there in 9? 18 * 1 = 8, 9 - 8 = 1 remaining 4. How many 4s are there in 1? 05. How many 2s are there in 1? 06. Leaving 111 2510 = 1100123/22/201010Copyright 2010 Steven T. Jones

11. Octal is based on powers of 88382818084512s64s8s1s4096s...335313 X 1 = 35 X 8 = 403 X 64 = 1623 X 512 = 15361 X 4096 = 40965837103/22/201011Copyright 2010 Steven T. Jones

12. Converting 583710 to Base8The first six powers of 8:80= 1, 81= 8, 82= 64, 83= 512, 84= 4096, 85=327681. How many 32768s are there in 5837? none2. How many 4096s are there in 5837? 14096 * 1 = 4096, 5837 - 4096 = 1741 remaining 3. How many 512s are there in 1741? 3512 * 3 = 1536, 1741 - 1536 = 205 remaining 4. How many 64s are there in 205? 364* 3 = 162, 205 - 162 = 43 remaining 5. How many 8s are there in 43? 58* 5 = 40, 43 - 40 = 31s 35,83710 = 13,35383/22/201012Copyright 2010 Steven T. Jones

13. Hexadecimal is based on powers of 161631621611601644096s256s16s1s65536s...16CDD X 1 = 13C X 16 = 1926 X 256 = 15361 X 4096 = 40960 X 65536 = 05837103/22/201013Copyright 2010 Steven T. Jones

14. Converting 583710 to Hexadecimal The first five powers of 16:160= 1, 161= 16, 162= 256, 163= 4096, 164= 655361. How many 65536s are there in 5837? none2. How many 4096s are there in 5837? 1 4096 * 1 = 4096 , 5837 - 4096 = 1741 remaining 3. How many 256s are there in 1741? 6 256 * 6 = 1536, 1741 - 1536 = 205 remaining 4. How many 16s are there in 205? C (1210)16 * 12 = 192, 205 - 192 = 131s D (1310) 583710 = 16CD163/22/201014Copyright 2010 Steven T. Jones

15. Bits and Nybbles1 bit = 1 binary digit, possible values: 0, 1 (010 - 110)2 bits = 2 binary digits, possible values:00, 01, 10, 11 (010 - 310)3 bits = 3 binary digits, possible values:000, 001, 010, 011, 100, 101, 110, 111 (010 - 710)nybble (½ byte) = 4 bits = 4 binary digits, possible values: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111(010 - 1510)3/22/201015Copyright 2010 Steven T. Jones

16. Bytes and Words1 byte = 8 binary digits, possible values: (010 - 25510)2 bytes (standard C unsigned int) = 16 binary digits, possible values:(010 - 32,76810)4 bytes (standard C unsigned long) = 32 binary digits, possible values:(010 - 2,147,483,64810)For our purposes, a word is a unit of data made up of more than one byte3/22/201016Copyright 2010 Steven T. Jones

17. Growing Binary Numbers into Hex (Bits 1-3)One Bit, Two Combinations (0 and 1):00000001 010 110Add a Red Bit (0 and 1) to Each Combination:0000000100100011 010 110 210 310Add a Blue Bit (0 and 1) to Each New Combination:0000000100100011 0100010101100111 010 110 210 310 410 510 610 7103/22/201017Copyright 2010 Steven T. Jones

18. Growing Binary Numbers into Hex (Bit 4)Add a Green Bit (0 and 1) to Each New Combination:00000001001000110100010101100111 010 110 210 310 410 510 610 710 016 116 216 316 416 516 616 71610001001101010111100110111101111 810 910 1010 1110 1210 1310 1410 1510 816 916 A16 B16 C16 D16 E16 F16A hexadecimal digit can be thought of as a shorthand notation for a group of 4 bits (a “nybble”)Therefore, a byte (8 bits) can always be represented by 2 hex digits and a “standard” C integer (16 bits) can be represented by 4 hex digits (see next slide)3/22/201018Copyright 2010 Steven T. Jones

19. Proving the ShorthandBinary 00100010 = 216216 Hexadecimal 22 =0 X 128 = 0 0 X 64 = 01 X 32 = 32 0 X 16 = 00 X 8 = 0 0 X 4 = 0 1 X 2 = 20 X 1 = 0342 X 16 = 322 X 1 = 23401111101= 0 X 128 = 0716D16 1 X 64 = 641 X 32 = 32 1 X 16 = 161 X 8 = 8 1 X 4 = 4 0 X 2 = 01 X 1 = 1125 7D = 7 X 16 = 112D (13) X 1 = 131253/22/201019Copyright 2010 Steven T. Jones

20. Octal Shorthand for 6-Digit Binary NumbersBinary 010010 = 2828 Octal 22 =0X 32 = 01 X 16 = 160 X 8 = 0 0 X 4 = 0 1 X 2 = 20 X 1 = 0182 X 8 = 162 X 1 = 218101111 1 X 32 = 325878 0 X 16 = 01 X 8 = 81 X 4 = 4 1 X 2 = 21 X 1 = 14757= 5 X 8 = 407 X 1 = 7473/22/201020Copyright 2010 Steven T. Jones

21. Shorthand Notations Work Because ...Powers of 8 (1, 8, 64, 512, etc.) are also powers of 21 = 20; 8 = 23; 64 = 26; etc.Powers of 16 (1, 16, 256, 4096, etc.) are also powers of 21 = 20; 16 = 24; 256 = 28; etc.Every third power of 2 is a power of 8Every fourth power of 2 is a power of 16See next two slides

22. Exponential Correlations of 2 and 8First 17 Powers of 2:20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128, 28=256, 29=512, 210=1,024, 211=2,048, 212=4,096, 213=8,192, 214=16,384, 215=32,768, 216=65,536First 6 Powers of 8:80=1,81=8,82=64,83=512,84=4,096,85=32,7683/22/201022Copyright 2010 Steven T. Jones

23. Exponential Correlations of 2, 8, and 16First 17 Powers of 2 (powers of 8 underscored):20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128,28=256, 29=512, 210=1,024, 211=2,048, 212=4,096, 213=8,192, 214=16,384, 215=32,768, 216=65,536First 5 Powers of 16:160=1,161=16,162=256,163=4,096,164=65,5363/22/201023Copyright 2010 Steven T. Jones

24. The Trouble with DecimalsComputers are binary devicesThe decimal values 0 and 1 can be accurately and efficiently stored as binary numbers – as 0 and 1 (20)No other powers of 10 correspond to powers of 2, so ,unlike bases 2, 8, and 16, no direct equivalents existComputers either store approximations of decimal numbers or they store them a digit at a time – see next slide

25. Storing Decimal Numbers AccuratelyValue BinaryDecimal 71000000111000001117 7 14100000111000000001000001001414 471000101111000001000000011147 4 7 12810100000000000000100000010000010001281283/22/201025Copyright 2010 Steven T. Jones

26. http://www.kokomobeach.com