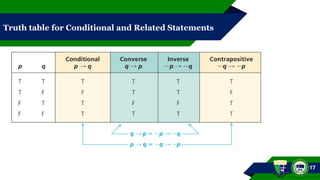
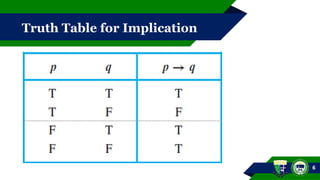
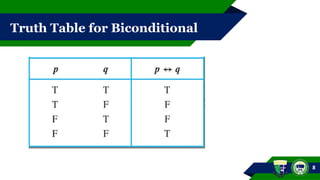
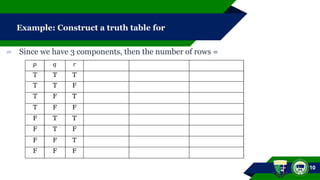
This document outlines concepts of implication, biconditional statements, and logical equivalence within the field of mathematics. It explains the structure and truth values of conditional statements, provides examples on how to determine antecedents and consequents, and discusses truth tables. It also covers the converse, inverse, and contrapositive of implications, including practical applications in examples.

1. Jayson R. Sarin
Faculty, Mathematics and Science Division
jrsarin@urios.edu.ph
Implication, Biconditional
and Logical Equivalence
Father Saturnino Urios University
Arts and Sciences Program
GE 104: Mathematic in the Modern World

2. Connective # 4: Implication (symbol )
▰ If p and q are statement variables, the symbolic form of
“if p then q” is p q. This may also be read “p implies q”, “p only
if q or “if p, q”.
▰ Here p is called the hypothesis/antecedent statement and q is
called the conclusion/consequent statement.
▰ It is also called as conditional statement.
▰ “If p then q” is false when p is true and q is false, and it is true
otherwise.
▰ Note: p q is true if p is false, regardless of the truth of q.
2

3. Example 1: Identify the Antecedent and Consequent of an
Implication
a. If our school was this nice, I would go there more than once a week.
b. If you don’t stop and look around once in a while, you could miss it.
c. If you strike me down, I shall become more powerful than you can possibly.
Solution:
a. Antecedent: our school was this nice
Consequent: I would go there more than once a week
b. Antecedent: you don’t stop and look around once in a while
Consequent: you could miss it
c. Antecedent: you strike me down
Consequent: I shall become more powerful than you can possibly
3

4. Example 2:
If Ms. X passes the exam, then she will get the job.
▰ Here q is She will get the job and p is Ms. X passes the exam.
▰ The statement states that Ms. X will get the job if a certain condition
(passing the exam) is met; it says nothing about what will happen if the
condition is not met. If the condition is not met, the truth of the
conclusion cannot be determined; the conditional statement is
therefore considered to be vacuously true, or true by default.
4

5. Example 3: Determine the truth value of an
Implication
a. If 2 is an integer, then 2 is a rational number.
b. If 3 is a negative number, then .
c. If , then
Solution:
a. Because the consequent is true, this is a true statement.
b. Because the antecedent is false, this is a true statement.
c. Because the antecedent is true and the consequent is false, this is a false
statement.
5

6. Truth Table for Implication
6

7. Connective # 5: Biconditional (symbol )
▰ If p and q are statement variables, the symbolic form
of “p if and only if q” is denoted by p q.
▰ It is true if both p and q have the same truth values.
▰ Note: p q is a short form for (p q) (q p)
7

8. Truth Table for Biconditional
8

9. Example: Determine the truth value of a Biconditional
a. if and only if .
b. if and only if .
Solution:
a. Because components are true when and both are false when . This is a
true statement.
b. If , the first component is true and the second component is false. This is
a false statement.
9

10. Example: Construct a truth table for
▰ Since we have 3 components, then the number of rows =
10

11. Example: Construct a truth table for
▰ A tautology is a logical proposition that is always true.
▰ A contradiction is a logical proposition that is always false.
11

12. Logical Equivalence
▰ Compound propositions r and s are logically equivalent if the
statement r s is a
↔ tautology.
▰ If r and s are logically equivalent, we write r s
⇔ .
▰ A second notation often used to mean statements r and s are logically
equivalent is r s
≡ .
▰ We used the symbol or to indicate statements r and s are not logically
equivalent
▰ You can determine whether compound propositions r and s are logically
equivalent by building a single truth table for both propositions and
checking to see that they have exactly the same truth values.
12

13. Example 1:
Show that (p q) (q p) is logically equivalent to p q.
→ ∧ → ↔
Solution: Show the truth values of both propositions are identical.
13
It shows that [(p q) (q p)]
→ ∧ → (
⇔ p q)
↔ .

14. Example 2:
Show ¬(p q) is equivalent to p ¬q.
→ ∧
Solution: Build a truth table containing each of the statements.
14
We proved that ¬(p q)
→ (
⇔ p ¬q).
∧

15. The Converse, the Inverse, and the Contrapositive
Statements related implication/conditional statement:
▰ The converse of is
▰ The inverse of is
▰ The contrapositive of is
The above definitions show the following:
■ The converse of p q
→ is formed by interchanging the antecedent p with the consequent q.
The inverse of
■ p q
→ is formed by negating the antecedent p and negating the consequent q.
The contrapositive of
■ p q
→ is formed by negating both the antecedent p and the
consequent q and interchanging these negated statements.
15

16. Example:
Write the converse, inverse and, contrapositive of:
If I get a job, then I will rent the apartment.
Solution:
Converse: If I rent the apartment, then I get the job.
Inverse: If I do not get the job, then I will not rent the apartment.
Contrapositive: If I do not rent the apartment, then I did not get the job.
16

17. Truth table for Conditional and Related Statements
17

18. Example:
Solution:
a. If a and b are both divisible by 5, then is divisible by 5.
 This is a true statement, so the original statement is also true.
b. If is an even integer, then is an even integer.
 This is a true statement, so the original statement is also true.
18

19. References:
Aufmann, R.N., Lockwood, J. S., Nation, R.D., Clegg, D.K. “Mathematical Excursions” (3rd
edition), Brooks Cole CENGAGE Learning
Baltazar, E. C., Ragasa, C., Evangelista, J. (2018). Mathematics in the Modern World. C & E
Publishing Inc.
Nocon, R. C., & Nocon, E.G. (2018).Essential Mathematics of the Modern World. C & E
Publishing Inc.
Kwong, H. (2021). A spiral Workbook for Discrete Mathematics, OpenSUNY, accessed 24
November 2021,
https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/
A_Spiral_Workbook_for_Discrete_Mathematics_(Kwong)
19