More Related Content
PDF
PPTX
【DL輪読会】時系列予測 Transfomers の精度向上手法 PDF
Deep State Space Models for Time Series Forecasting の紹介 PPTX
【DL輪読会】Flow Matching for Generative Modeling PDF
PPTX
PDF
PDF
[DL輪読会]Control as Inferenceと発展 What's hot
PDF
【論文紹介】 Attention Based Spatial-Temporal Graph Convolutional Networks for Traf... PDF
最近のDeep Learning (NLP) 界隈におけるAttention事情 PDF
Neural networks for Graph Data NeurIPS2018読み会@PFN PPTX
PDF
SSII2022 [TS1] Transformerの最前線〜 畳込みニューラルネットワークの先へ 〜 PPTX
Dimensionality reduction with t-SNE(Rtsne) and UMAP(uwot) using R packages. PDF
PDF
PDF
cvpaper.challenge 研究効率化 Tips PDF
PDF
[DL輪読会]自動運転技術の課題に役立つかもしれない論文3本 PPTX
PPTX
PDF
PDF
遺伝的アルゴリズム�(Genetic Algorithm)を始めよう! PDF
Skip Connection まとめ(Neural Network) PDF
PDF
PDF
PPTX
Similar to K shapes zemiyomi
PDF
Cluster Analysis at REQUIRE 26, 2016/10/01 PPT
Tokyo r#10 Rによるデータサイエンス 第五章:クラスター分析 PDF
第3回集合知プログラミング勉強会 #TokyoCI グループを見つけ出す PDF
ユークリッド距離以外の距離で教師無しクラスタリング PDF
PDF
PDF
PDF
PDF
Visualizing Data Using t-SNE PDF
はじめてのパターン認識 第5章 k最近傍法(k_nn法) PDF
PDF
無限関係モデル (続・わかりやすいパターン認識 13章) PPTX
PDF
PDF
Deformable Part Modelとその発展 PPTX
Clustering of time series subsequences is meaningless 解説 PPTX
PDF
PDF
NIPS2013読み会: Scalable kernels for graphs with continuous attributes PDF
K shapes zemiyomi
- 1.
- 2.
- 3.
扱う問題は何か?
K-shapeは時系列データのクラスタリング手法
3
𝒕 𝟏 ……𝒕 𝒎
𝑥1 3000 ・・
・
4000
…. ・・
・
・・
・
𝑥 𝑛 2000 ・・
・
1000
●時系列データ
𝑡 = 時刻 (=次元数)
𝑥 = 観測点
ex)例えば、特徴ベクトル𝑥をある
商品の一年間の売り上げとすると、
𝑥
の𝑖番目の要素が、𝑡𝑖日目でのその
商品の売り上げ高となる。
要素数は365である。
時系列クラス
タリング
同様の傾向に
ある時系列を
いくつかのク
ラスタに分割
する。
m次元空間に書
き直すと、、、
- 4.
- 5.
- 6.
- 7.
既存のアプローチ_距離の測り方
時系列データ間の距離を測る際の代表的指標
7
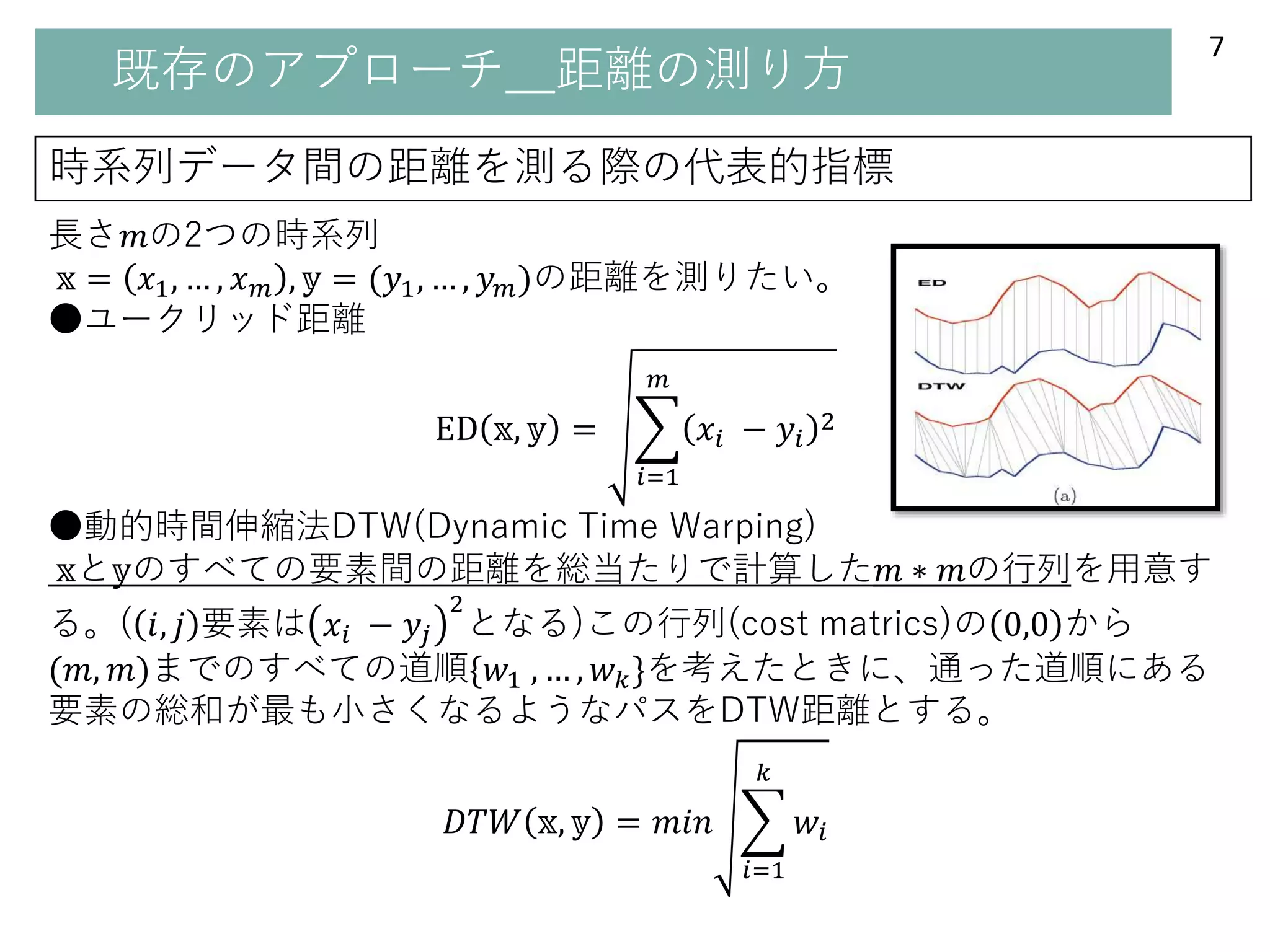
長さ𝑚の2つの時系列
𝕩 = 𝑥1,… , 𝑥 𝑚 , 𝕪 = (𝑦1, … , 𝑦 𝑚)の距離を測りたい。
●ユークリッド距離
ED 𝕩, 𝕪 =
𝑖=1
𝑚
𝑥𝑖 − 𝑦𝑖
2
●動的時間伸縮法DTW(Dynamic Time Warping)
𝕩と𝕪のすべての要素間の距離を総当たりで計算した𝑚 ∗ 𝑚の行列を用意す
る。( 𝑖, 𝑗 要素は 𝑥𝑖 − 𝑦𝑗
2
となる)この行列(cost matrics)の 0,0 から
(𝑚, 𝑚)までのすべての道順{𝑤1 , … , 𝑤 𝑘}を考えたときに、通った道順にある
要素の総和が最も小さくなるようなパスをDTW距離とする。
𝐷𝑇𝑊 𝕩, 𝕪 = 𝑚𝑖𝑛
𝑖=1
𝑘
𝑤𝑖
- 8.
- 9.
- 10.
既存のアプローチ_アルゴリズム種類
10
●feature- and model-basedmethods
典型的なアルゴリズムに良く当てはまるようにデータの方を変換する。
混合正規分布など??
●raw-based methods
時系列データに最も適合するよう、アルゴリズムの距離の測り方を変える。
・階層的クラスタリングex)ウォード法、群平均法、最短(最長)距離法等
最も類似度が高い点の組み合わせからまとめていく手法
・分割最適化クラスタリングex)k-means、 k-medoids
いくつのクラスターに分けるかあらかじめ定め、定めたクラスター数にな
るようにまとめていく手法
・スぺクトラルクラスタリング
グラフの連結構造を利用したクラスタリング
K-shapesはraw- basededアルゴリズム
⇒なぜか??
⇒raw-badedの方がデータの種類を問わず使用できる(domain-independent)
- 11.
- 12.
- 13.
- 14.
k-SHAPE_②相互相関をもとにした距離
14
Cross-correlation measure(相互相関測度)
𝕩 =𝑥1, … , 𝑥 𝑚 , 𝕪 = (𝑦1, … , 𝑦 𝑚)の距離を測りたい。
⇒単純な距離を測ると、右下図のような類似性を考慮できない。
⇒𝕪(あるいは𝕩)を時間軸mに沿って,平行移動させ、平行移動させた後の内
積的な類似度を測る。
●定義
𝑤 − 𝑚 (= 𝑑𝑒𝑓 𝑘)回、𝕪を右に平行移動させたとき(𝕪の時間を進めたとき)の
𝕩との類似度𝐶𝐶 𝑤(𝕩, 𝕪)を以下で定義する。
𝐶𝐶 𝑤 𝕩, 𝕪 = 𝑅 𝑤−𝑚(𝕩, 𝕪)
𝑅 𝑘 𝕩, 𝕪 =
𝑙=1
𝑚−𝑘
𝑥𝑙+𝑘 . 𝑦𝑙
𝑅−𝑘(𝕪, 𝕩)
類似度𝐶𝐶 𝑤(𝕩, 𝕪)を𝑤 ∈ 1, 2, … , 2𝑚 − 1
で計算する。(𝐶𝐶 𝑤 𝕩, 𝕪 , … . , 𝐶𝐶2𝑚−1(𝕩, 𝕪))
このうち最も大きいものを相互相関とする
Kが負のときは、x
とyが逆になり、y
の時間をk巻き戻す。
(xの時間をk進め
る。)
- 15.
- 16.
- 17.
- 18.
- 19.
k-SHAPE_③クラスタ中心(centroid)の計算 19
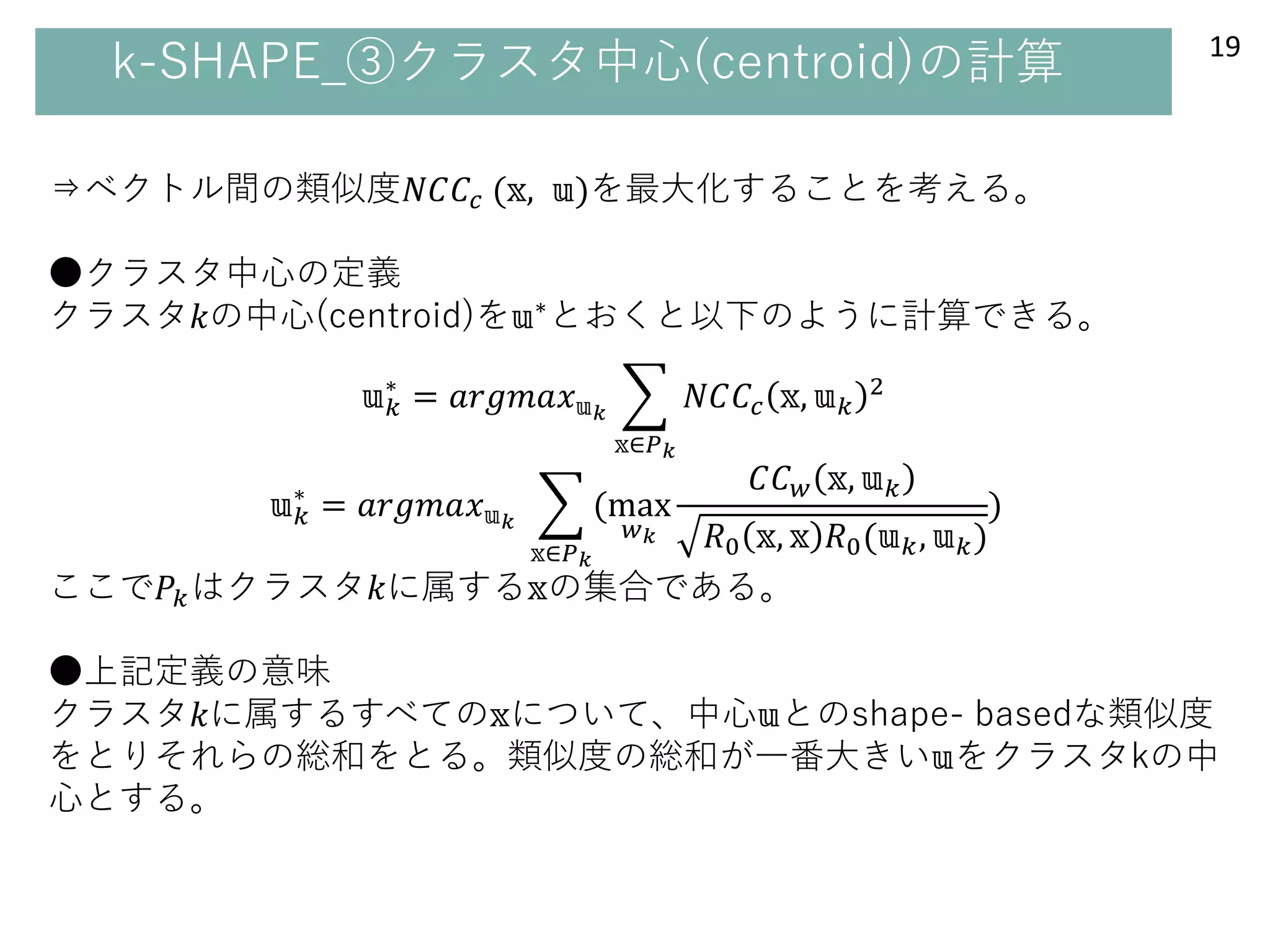
⇒ベクトル間の類似度𝑁𝐶𝐶𝑐 (𝕩,𝕦)を最大化することを考える。
●クラスタ中心の定義
クラスタ𝑘の中心(centroid)を𝕦∗とおくと以下のように計算できる。
𝕦 𝑘
∗
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝕦 𝑘
𝕩∈𝑃 𝑘
𝑁𝐶𝐶𝑐 𝕩, 𝕦 𝑘
2
𝕦 𝑘
∗
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝕦 𝑘
𝕩∈𝑃 𝑘
(max
𝑤 𝑘
𝐶𝐶 𝑤 𝕩, 𝕦 𝑘
𝑅0 𝕩, 𝕩 𝑅0(𝕦 𝑘, 𝕦 𝑘)
)
ここで𝑃𝑘はクラスタ𝑘に属する𝕩の集合である。
●上記定義の意味
クラスタ𝑘に属するすべての𝕩について、中心𝕦とのshape- basedな類似度
をとりそれらの総和をとる。類似度の総和が一番大きい𝕦をクラスタkの中
心とする。
- 20.
k-SHAPE_③クラスタ中心(centroid)の計算 20
𝕦∗ =𝑎𝑟𝑔𝑚𝑎𝑥 𝕦 𝑘
𝕩∈𝑃 𝑘
(
max
𝑤
𝐶𝐶 𝑤 𝕩, 𝕦 𝑘
𝑅0 𝕩, 𝕩 𝑅0(𝕦 𝑘, 𝕦 𝑘)
)
⇒このままだと、𝕦 𝑘も𝑤も動くので計算が難しい。
⇒前のループで計算した𝕦∗が次の𝕦∗に近いという仮定のもと、一旦、赤枠
の部分を𝕦 𝑘 = (前の𝕦∗)として考える。
⇒分子は、前の𝕦∗との類似度が最大となるよう𝑥をスライドさせる。分母
は、 𝑅0 𝕩, 𝕩 𝑅0(𝕦∗, 𝕦∗) = (定数)なので消せる。
⇒ 前の𝕦∗ = 𝕦 𝑘に戻す。
𝕦∗
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝕦
𝑥∈𝑃 𝑘 𝑙∈ 1,𝑚
𝑥𝑖𝑙 𝑢 𝑘𝑙
2
⇒レイリー商の形に帰着でき、最大を求められる形になる(論文式14、15)
𝕦∗
= 𝑎𝑟𝑔𝑚𝑎𝑥 𝕦
𝕦 𝑇
・𝑀・𝕦
𝕦 𝑇・ 𝕦
正しくないか
も。。。
- 21.
Editor's Notes
- #4 目的:扱う問題をつかんでもらう
●メッセージ
K-SHAPEで扱う問題=①時系列データの②クラスタリング
●詳細
①時系列データ??
・左上表のとおり
・ex)x1,x2がカレー、イチゴの一年間の売り上げ
t1,t2がいつの売り上げか
・横が一つの系列(=一本の線)=観測時間数分の要素数をもつベクトル
それらがn個集まったもの=クラスタリングする時系列データ
②クラスタリング??
・その時系列データで同様の傾向をもつもの同士をグルーピングする=時系列クラスタリング
・時系列で書くと特殊なことをやっているようにみえる。
⇒m次元空間に書きなおすと普通のクラスタリングと変わらない。
- #5 目的:既存のアプローチの概要をつかんで、後のプレゼンをわかりやすくする。
●メッセージ
時系列クラスタリングを考える2つのアプローチ=①クラスタリングアルゴリズム自体を工夫②距離の測り方を工夫
●詳細
①クラスタリングアルゴリズム自体を工夫
要するに、k-meansを使うのか、ウォード法をつかうのか、といったことです。
②距離の測り方の食う負
すでにあるクラスタリングで、距離を測る部分であったり、中心を更新する部分の数式を変えること。
- #6 では、まず距離の測り方から詳しく見ていこうと思います。
- #7 目的:距離の測り方が時系列クラスタリングにおいて重要な問題であることを理解してもらう
●メッセージ
時系列がもつ①様々な歪みに対応する距離尺度を用いる必要があるから
●詳細
歪み??不変性??
①具体例=付録
代表的なもの=(I)スケーリングと平行移動(Ⅱ)シフト不変性
いま=時系列xとyの類似度を比べたい
(I)スケーリングと平行移動
Xが縦方向に延びたり、縦方向に移動したりしても⇒類似性変わらない
(Ⅱ)シフト不変性
Xが横方向に移動してしまっても、⇒類似性が変わらない
という性質
②ほかにも、統一スケールや欠損、複雑性に対しても不変性を備える必要があります。
- #8 目的:時系列データに対する既存の距離尺度を理解してもらう
●メッセージ
時系列データに対する既存の距離尺度=①ユークリッド距離②動的時間伸縮法
③ユークリッド距離よりもDTWの方が、時系列の歪みをよく捉えられている。
●詳細
①ユークリッド距離??
普通のk-meansで扱われる手法
みなさんご存じ
②動的時間伸縮法
定義はいったん置いておいて、、、
時間が異なる要素間の距離を測っているというのがEDと異なる点
⇒③右上図にある通り、ED=同じ時間の距離を測ってる⇔DTW=異なる時間の距離を測ってる
⇒シフト不変性の考慮
- #9 目的:DTWの計算方法を理解してもらう
●メッセージ
DTWは、①costmatrixの計算と②distancematrixの計算から成る。
亜種として③cDTWというのがある。
●詳細
左図を中心に説明。
①costmatrixの計算
対象となる2つの時系列のすべての要素の組み合わせの距離を計算する
横軸=赤の線のposition
縦軸=青の線のposition
②distancematrixの計算
⇒詳しくは付録2を見てほしい。
③cDTWについて
あきらかに遠回りするような道が距離コスト最小とは考えずらい
⇒あらかじめ通る道順に制限を加えたものがcDTW
- #10 次は時系列クラスタリングで使われるアルゴリズムの方を見ていきたいと思います。
- #11 目的:クラスタリングアルゴリズムの種類とdomain性を理解してもらう
●メッセージ
アルゴリズムは大きく分けて2つ①モデルベースの方法②データベースの方法がある
そして、③扱うデータの種類を問わないのはデータベースの方である
●詳細
①モデルベースの方法
⇒データの方を変更する
②raw-basedmethodの方法
⇒データに大きな変更を加えずに、アルゴリズムの特に距離尺度に対する変更を加える。
⇒③データをいじるモデルベースの方法よりもraw-basedの方がデータの種類を問わず適応できることになる。
- #12 それでは、K-shapeの中身の方に移っていきたいと思います。
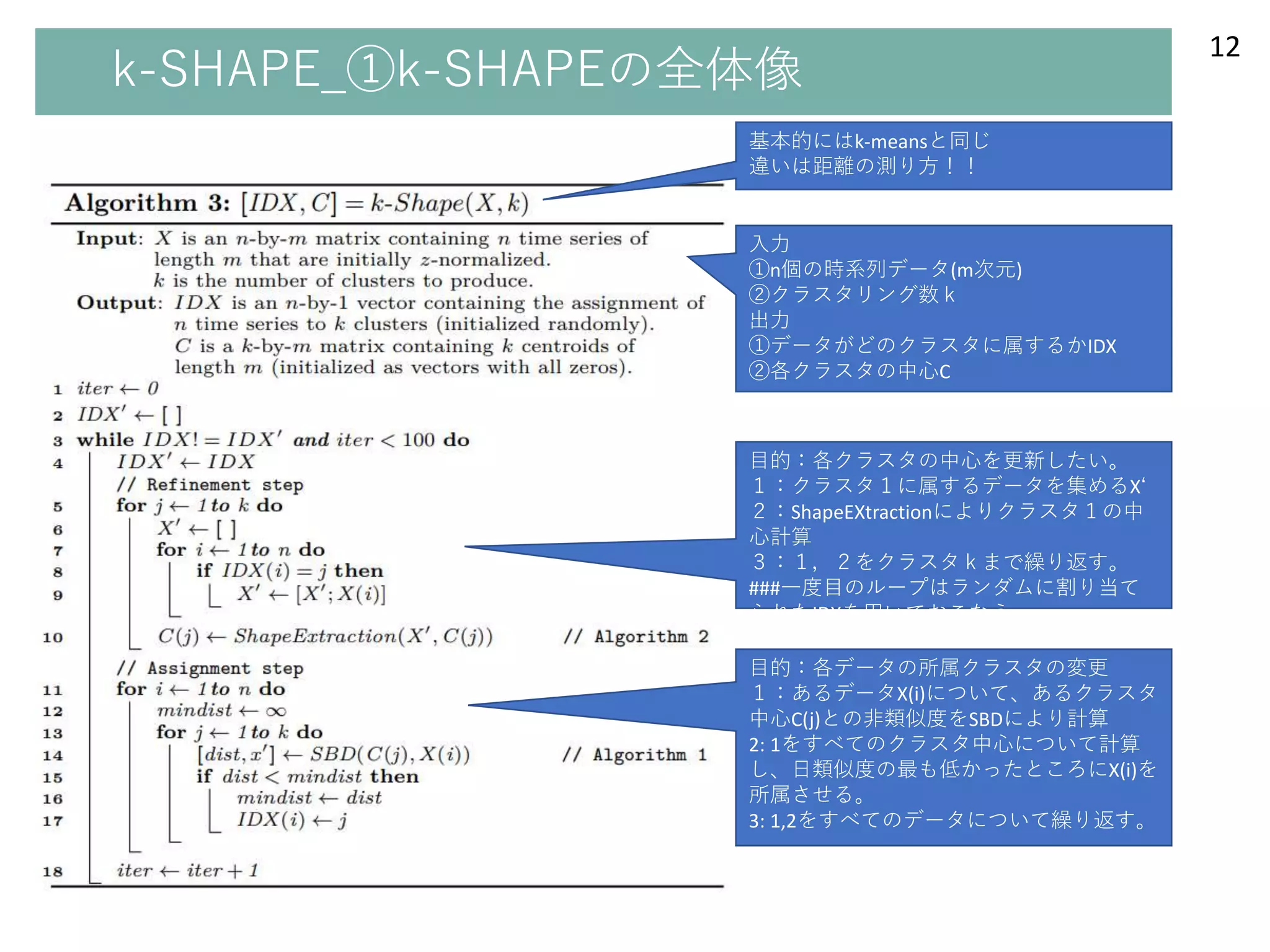
- #13 目的:k-shapeの全体像を理解してもらう
●メッセージ
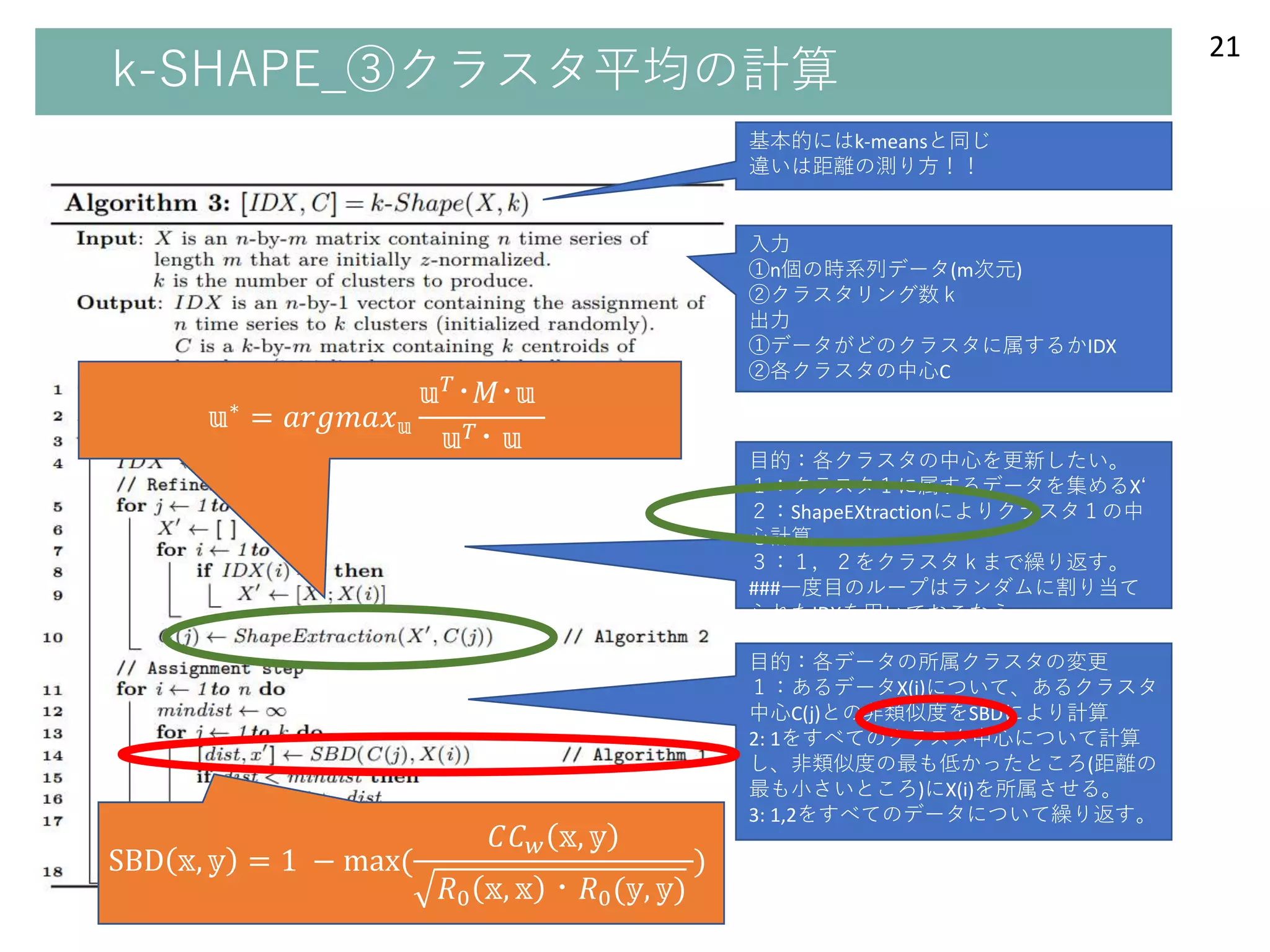
①基本的にはk-meansとアルゴリズムの全体は同じ
②相互相関に基づいた距離尺度と中心の計算を用いていることが異なる。
●詳細
1入力と出力の説明
2refinementstepの説明
中心を更新するとき、、、
K-meansだと幾何平均⇔ShapeExtractionというアルゴリズムを用いている
3assignment stepの説明
中心から各データへの距離を測るとき、、、
K-meansだとユークリッド距離⇔SBDという距離尺度で
- #14 まず、SBD(shape based distriction)から説明したいと思います。
- #15 目的:相互相関測度の考え方を理解してもらう
●メッセージ
相互相関測度は、時系列データの歪みにうまく適応するよう、時系列のスライドを行う。
●詳細
①右図=人間の目で見れば、類似していることは一目瞭然
⇒単純なユークリッド距離では類似性をとらえられない
⇒一方の時系列を平行移動させて、カチットはまったところで内積的な類似度を測ることを考える。
②定義はこちらです。。。
⇒わかりずらいと思うので、付録3を参照してください。
- #16 目的:正規化の種類と重要性を伝える。
●メッセージ
正規化には3種類あり、種類によって、どの程度のスライドが行われるかが決まる。
●詳細
①時系列の長さで正規化するNCCb、スライド数を考慮したNCCu、対象となる時系列の大きさで正規化したNCCcがある
②右下図をみると、正規化の仕方により、どの程度のスライドが相互相関を最大化させるかがかわってくる。
⇒aが入力する時系列2つです。動かさなくても大丈夫なことがわかる。
⇒b、c、dがそれぞれこの3つの正規化された相互相関に対応してる。
⇒横軸=w(最大値が真ん中から右にくると、yを右方向にすらいど、ちょうど真ん中だと変化なし、真ん中から左にくるとyを左方向にスライド)
縦軸=相互相関の値
⇒b、c、dそれぞれ検証
⇒結果的にNCCcが最適
- #17 目的:k-SHAPEの定義と意味を伝える。
●メッセージ
SBDはええぞ
●詳細
スライド通りにしゃべればよい。
SBD=0or2のときの状態⇒添付4
シフト不変性の説明
高速化については、追えなかったことを報告
- #18 次に、クラスタ中心の計算について説明を行います。
- #19 目的:クラスタ中心を計算する際に、①幾何平均ではうまくいかず、②相互相関を使うべきことを理解してもらう。
●メッセージ
①左図、青色の線=幾何平均でのクラスタの中心⇒右図の形の中心とは言えない!
②左図、黄色破線=相互相関をもとにした中心⇒右図の形をうまくとらえられているといえる。
- #20 じゃあ、それってどうやって計算するの??
目的:相互相関に基づいた中心概念を理解してもらう
●メッセージ
①クラスタ中心の定義②その意味
●詳細
①クラスタ中心uの定義はこんな感じです。
②意味はスライドにある通り。
- #21 ここからは、先ほど定義したuを実際に計算できる形に変形するフェイズです。
- #22 全体像としては、このような形です。
K-meansに対して、時系列の歪みを考慮した距離計算と中心の計算ができています。