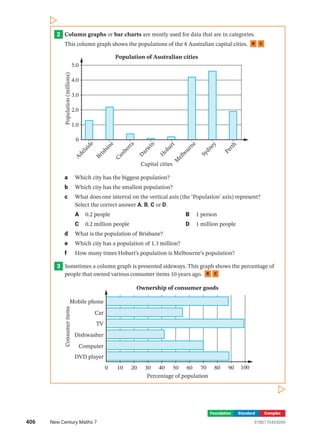
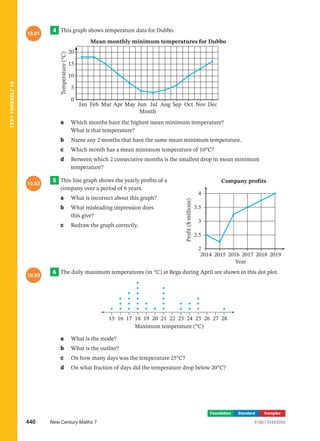
The document outlines statistical methods used for analyzing data relevant to decision-making, such as interpreting and presenting various types of graphs, calculating measures of central tendency (mean, median, mode), and identifying potential misleading graphs. It covers topics like dot plots, stem-and-leaf plots, and divided bar graphs, emphasizing the importance of statistics in applications ranging from government to businesses. Additionally, it discusses the interpretation of data from surveys and the implications of using statistics for effective communication and decisions.