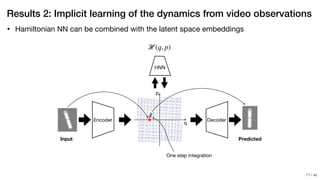
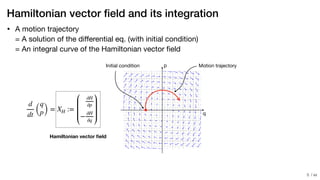
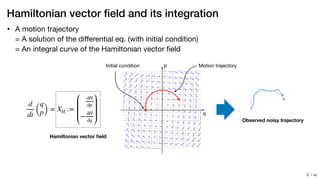
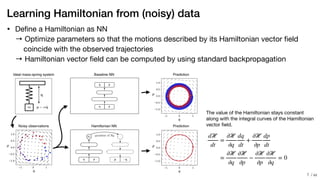
- Standard machine learning models do not guarantee satisfying physical conservation laws for motion prediction. - The paper proposes learning the "equations of motion" in the form of a Hamiltonian function using neural networks to predict trajectories that obey conservation laws. - The learned Hamiltonian function is integrated on the fly to generate predictions, ensuring the predictions satisfy conservation of energy.

1. / xx
Hamiltonian Neural Networks
Sam Greydanus, Misko Dzamba, Jason Yosinski
NeurIPS 2019 paper reading
2020/01/31 Kohta Ishikawa
!1

2. / xx
One-page summary
For those who are not familiar with the Hamiltonian mechanics…
• Standard ML-based prediction models do not guarantee to satisfy physical conservation laws.
• Enforcing corresponding costs or regularizers does not achieve exact conservation.
• Instead of learning motion predictors directly, learn “equations of motion” that the observed
trajectories obey.
• Motion prediction can be done by solving learned equations of motion on the fly.
• Predictions from “equations of motion” inevitably satisfies conservation laws.
How to get a physically consistent (energy preserving) motion predictor.
Learn Hamiltonian function ( ) from data as NN, and integrate Hamilton’s eq.
to predict.
Problem:
Idea:
Result: Learned small/large physical systems from the direct (qt, pt) observation.
Implicitly learned physical pendulum system from the video observation.
H : (q, p) ↦ E
!2

3. / xx
• Three different representations of the same physical law
Newtonian, Lagrangian, and Hamiltonian mechanics
F: Forcem
a: Acceleration
Newton’s law
ma = m
d2
x
dt2
= F
Lagrangian form Hamiltonian form
a =
d2
x
dt2
F = − ∇U : Conservative force
d
dt (
∂ℒ
∂ ·q )
−
∂ℒ
∂q
= 0
x : Position F : Force ℒ(q, ·q, t) := T − U : Lagrangian
q : Generalized coordinates
T : Kinetic energy (= 1/2 mv^2)
U: Potential energy
dq
dt
=
∂ℋ
∂p
dp
dt
= −
∂ℋ
∂q
ℋ(q, p, t) = p ·q − ℒ
: Hamiltonian
p :=
∂ℒ
∂ ·q
: Canonical
momentum
!3

4. / xx
• Three different representations of the same physical law
Newtonian, Lagrangian, and Hamiltonian mechanics
F: Forcem
a: Acceleration
Newton’s law
ma = m
d2
x
dt2
= F
Lagrangian form Hamiltonian form
a =
d2
x
dt2
F = − ∇U : Conservative force
d
dt (
∂ℒ
∂ ·q )
−
∂ℒ
∂q
= 0
x : Position F : Force ℒ(q, ·q, t) := T − U : Lagrangian
q : Generalized coordinates
T : Kinetic energy (= 1/2 mv^2)
U: Potential energy
dq
dt
=
∂ℋ
∂p
dp
dt
= −
∂ℋ
∂q
ℋ(q, p, t) = p ·q − ℒ
: Hamiltonian
p :=
∂ℒ
∂ ·q
: Canonical
momentum
!4

5. / xx
Hamiltonian vector field and its integration
• A motion trajectory
= A solution of the differential eq. (with initial condition)
= An integral curve of the Hamiltonian vector field
d
dt (
q
p) = XH :=
∂H
∂p
− ∂H
∂q
Hamiltonian vector field
Motion trajectoryInitial condition
q
p
!5

6. / xx
• A motion trajectory
= A solution of the differential eq. (with initial condition)
= An integral curve of the Hamiltonian vector field
Hamiltonian vector field and its integration
d
dt (
q
p) = XH :=
∂H
∂p
− ∂H
∂q
Hamiltonian vector field
Motion trajectoryInitial condition
Observed noisy trajectory
q
p
!6

7. / xx
Learning Hamiltonian from (noisy) data
• Define a Hamiltonian as NN
→ Optimize parameters so that the motions described by its Hamiltonian vector field
coincide with the observed trajectories
→ Hamiltonian vector field can be computed by using standard backpropagation
The value of the Hamiltonian stays constant
along with the integral curves of the Hamiltonian
vector field.
dℋ
dt
=
∂ℋ
∂q
dq
dt
+
∂ℋ
∂p
dp
dt
=
∂ℋ
∂q
∂ℋ
∂p
−
∂ℋ
∂p
∂ℋ
∂q
= 0
!7

8. / xx
Learning Hamiltonian from (noisy) data
• Data
• A set of trajectories that all of them (implicitly) come from the same Hamiltonian system
• Explicit time dependency of the Hamiltonian is not in consideration
• No dissipation is assumed
• Cost function
• The mean squared error of the predicted motion by the current Hamiltonian
• Assumed high temporal resolution observation (numerical derivative for data is used)
• In the author’s implementation, loss is computed in the integrated form with 4th-order Runge-
Kutta. Guess this is for dealing with coarse observation
• The noise model in observation is assumed to be iid Gaussian
Observation (Data)Prediction (Model)
!8

9. / xx
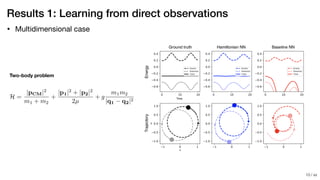
Results 1: Learning from direct observations
Ideal Harmonic Oscillator
Ideal Pendulum
Real Pendulum
Schmidt & Lipson [35]
Learned Hamiltonian
Ground Truth Hamiltonian
!9

10. / xx
Results 1: Learning from direct observations
• Multidimensional case
!10
Two-body problem

11. / xx
• Hamiltonian NN can be combined with the latent space embeddings
Results 2: Implicit learning of the dynamics from video observations
!11
Encoder Decoder
q
p
ℋ(q, p)
HNN
Input Predicted
One step integration

12. / xx
• Hamiltonian NN can be combined with the latent space embeddings
Results 2: Implicit learning of the dynamics from video observations
!12

13. / xx
One-page summary (again)
For those who are not familiar with the Hamiltonian mechanics…
• Standard ML-based prediction models do not guarantee to satisfy physical conservation laws.
• Enforcing corresponding costs or regularizers does not achieve exact conservation.
• Instead of learning motion predictors directly, learn “equations of motion” that the observed
trajectories obey.
• Motion prediction can be done by solving learned equations of motion on the fly.
• Predictions from “equations of motion” inevitably satisfies conservation laws.
How to get a physically consistent (energy preserving) motion predictor.
Learn Hamiltonian function ( ) from data as NN, and integrate Hamilton’s eq.
to predict.
Problem:
Idea:
Result: Learned small/large physical systems from the direct (qt, pt) observation.
Implicitly learned physical pendulum system from the video observation.
H : (q, p) ↦ E
!13