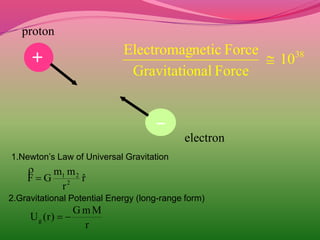
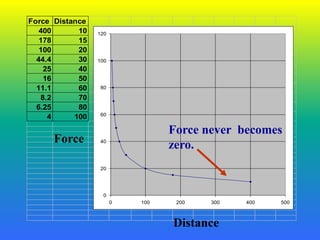
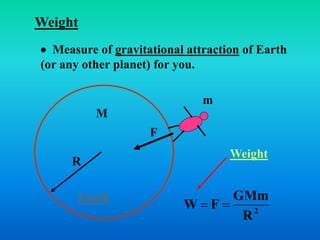
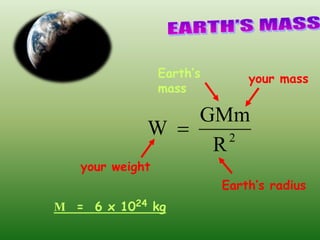
1. Isaac Newton discovered the law of universal gravitation, which explains that all masses in the universe attract each other with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.
2. Gravitational potential energy is defined as the work required to move an object away from a source of gravity. Near the earth's surface, the old and new forms of gravitational potential energy equations are equivalent when considering only changes in potential energy.
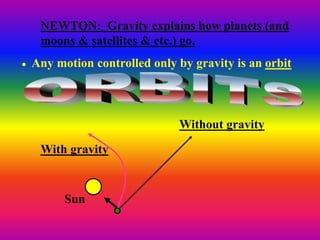
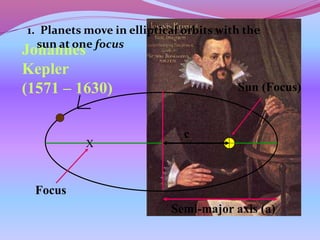
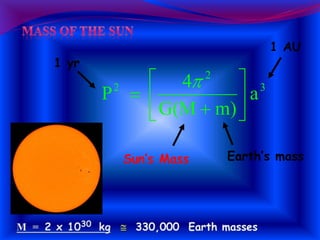
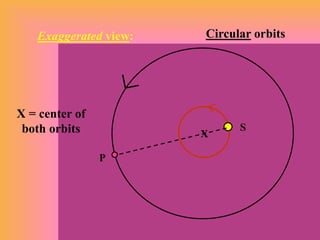
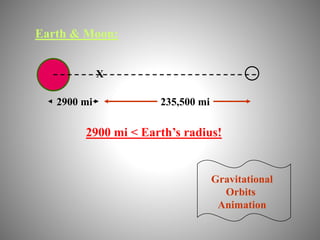
3. Newton's law of universal gravitation and the inverse square law explain how gravity causes orbits, from planets orbiting the sun to satellites orbiting the earth. The center of mass of two orbiting bodies actually orbits around the