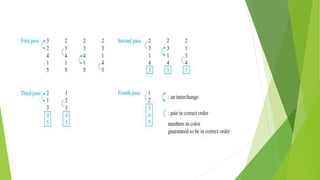
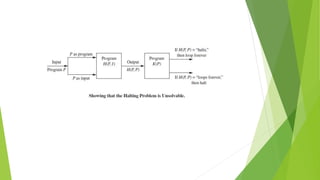
The document discusses algorithms, defining them as finite sets of precise instructions for performing computations or solving problems. It highlights key algorithms such as linear search, binary search, bubble sort, insertion sort, and greedy algorithms, along with their respective procedures and applications. Additionally, it introduces the concept of the halting problem, which is presented as an unsolvable issue in computational theory.

1. Discrete Mathematics And it’s Applications
Algorithms

2. Group # 01
BSIT-3rd –B-Morning
Members
 Muhammad Waqar Munir
 Rehan Ali
 Farooq Shah
 Jahanzaib Shahid
 Muhammad Hammad

3. Algorithms Methodology:
 Construct a model that translates the
problem into a mathematical context
 Build a method that will solve the
general problem using the model
 Ideally, we need a procedure that
follows a sequence of steps that leads
to the desired answer, such a
sequence is called an Algorithm.
History:
The term Algorithm is a corruption of the
name Al-Khowarizmi (mathematician of the
9th century)

4. Algorithms
 What is an algorithms?
An Algorithm is a finite set of precise instructions for performing a
computation or for solving a problem.

5. • Finding the Maximum Element in a Finite
Sequence
procedure max(a1, a2, . . . , an: integers)
max := a1
for i := 2 to n
if max < ai then max := ai
return max{max is the largest element}

6. Properties of algorithms:
 Inputfrom a specified set.
 Outputfrom a specified set (solution)
 Correctness of output for every possible input.
 Definiteness of evert step in the computation
 Effectiveness of each calculation step and
 Generality for a class of problems.

7. Searching Algorithms
 The problem of locating an element in an ordered list occurs in
many contexts. For instance, a
 program that checks the spelling of words searches for them in a
dictionary, which is just an
 ordered list of words. Problems of this kind are called searching
problems.

8. THE LINEAR SEARCH
The first algorithm that we will present is called the linear search,
or sequential search, algorithm.
• ALGORITHM For The Linear Search
procedure linear search(x: integer, a1, a2, . . . , an: distinct
integers)
i := 1
while (i ≤ n and x = ai )
i := i + 1
if i ≤ n then location := i
else location := 0
return location{location is the subscript of the term that equals
x, or is 0 if x is not found}

9. THE BINARY SEARCH
Some Instructions:
• if the
terms are numbers, they are listed from smallest to largest
• if they are words, they are listed
in lexicographic, or alphabetic, order
can be used when the list has terms occurring in order of
increasing size.

10. Binary Search
 May only b used on a sorted array.
 Eliminates one half of the elements after each comparison.
 Locate the middle of the array.
 Compare the value at that location with the search key.
 If they are equal-done.
 Otherwise, decide which half of the array contains the search key.
 Repeat the search on that half of the array and ignore the other half.
 The search continues until the key is matched or no elements remain to be
sorted.

11. • ALGORITHM For The Binary Search
procedure binary search (x: integer, a1, a2, . . . , an:
increasing integers)
i := 1{i is left endpoint of search interval}
j := n {j is right endpoint of search interval}
while i < j
m := (i + j)/2
if x > am then i := m + 1
else j := m
if x = ai then location := i
else location := 0
return location{location is the subscript i of the term ai
equal to x, or 0 if x is not found}

12. Sorting
 Goal
“Ordering the elements”
for example, sorting the list 7,2,1,4,5,9
produces the list 1,2,4,5,7,9.
Similarly, sorting of list d, h, c, a, f
produces a, c, d, f, h.

13. BUBBLE SORT
The bubble sort is one of the simplest
sorting algorithms, but not one of the most
efficient. It puts a list into increasing order by
successively comparing adjacent elements,
interchanging them if they are in the wrong
order.
The Bubble Sort algorithm looks at the pairs of entries in the
array, and swaps their order if needed.

15. • ALGORITHM For The Bubble Sort
procedure bubble sort(a1, . . . , an : real numbers with n ≥ 2)
for i := 1 to n − 1
for j := 1 to n − i
if aj > aj+1 then interchange aj and aj+1
{a1, . . . , an is in increasing order}

16. INSERTION SORT
• The insertion sort is a simple sorting
algorithm, but it is usually not the most
efficient.
• To sort a list with n elements,
• insertion sort begins with the second
element.

17. • ALGORITHM For Insertion Sort
procedure insertion sort(a1, a2, . . . , an:
real numbers with n ≥ 2)
for j := 2 to n
i := 1
while aj > ai
i := i + 1
m := aj
for k := 0 to j − i − 1
aj−k := aj−k−1
ai := m
{a1, . . . , an is in increasing order}

18. Greedy Algorithms
• to find a solution to the given problem that either
minimizes or maximizes the value of some
parameter
• one of the simplest approaches often leads to a
solution of an optimization Problem.
Algorithms that make what seems to be the “best” choice at each
step are called greedy algorithms.

19. • ALGORITHM For Greedy Change-
Making Algorithm
procedure change(c1, c2, . . . , cr : values
of denominations of coins, where
c1 > c2 > ・ ・ ・ > cr ; n: a positive
integer)
for i := 1 to r
di := 0 {di counts the coins of denomination
ci used}
while n ≥ ci
di := di + 1 {add a coin of denomination ci}
n := n − ci
{di is the number of coins of denomination
ci in the change for i = 1, 2, . . . , r}

20. TheHaltingProblem
• these are unsolvable problems, called halting
problem.
• a problem that cannot be solved using any
procedure.
• We will describe Turing’s proof that the halting
problem is unsolvable.