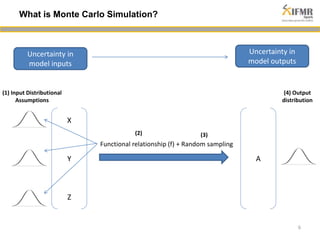
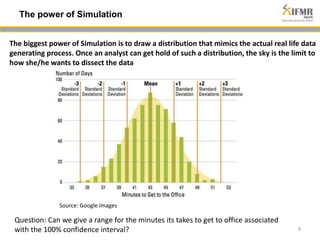
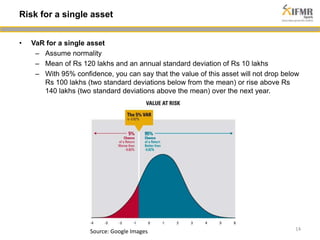
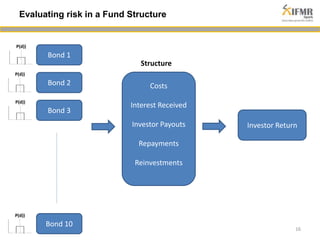
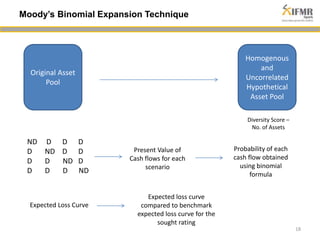
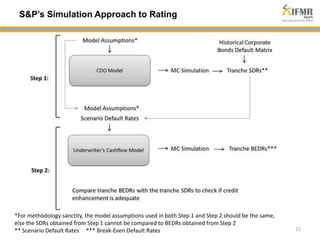
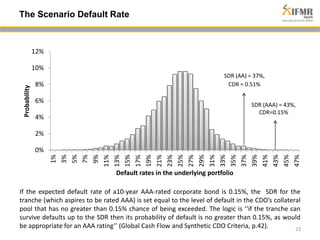
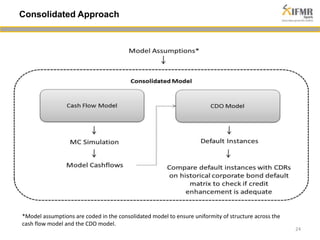
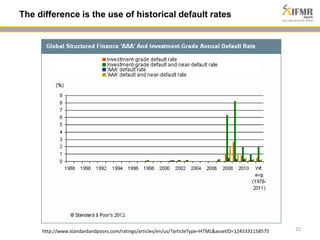
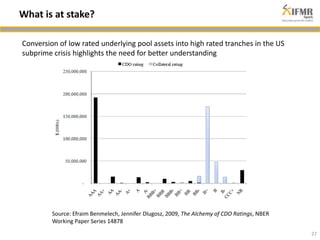
The document discusses methodologies for estimating default risk in fund structures, primarily through Monte Carlo (MC) simulations, scenario analysis, and decision trees. It highlights the advantages of simulations in managing uncertainty and assessing risks, as well as the specific techniques used for evaluating asset portfolios and credit default obligations (CDOs). Additionally, it addresses the limitations and criticisms of these methods, while emphasizing the importance of accurate data and assumptions in the simulation process.

1. Estimating Default Risk in Fund Structures
October 2014
Ravi Saraogi | IFMR Investments

2. Structure
2
 Refresher on MC Simulation
 Techniques for estimating default risk in Fund structures

3. • Suppose your commute to work consists of the following:
– Drive 3 kms on a highway, with 90% probability you will be able to average 20
KMPH the whole way, but with a 10% probability that a free road will result in
average speed of 80 KMPH.
– Come to an intersection with a traffic light that is red for 10 minutes, then green
for 3 minutes.
– Travel 1 km, averaging 50 KMMPH with a standard deviation of 10 KMPH.
– Come to an intersection with a traffic light that is red for 1 minutes, then green for
30 seconds.
– Travel 1 more km, averaging 30 KMMPH with a standard deviation of 5 KMPH.
You want to know how much time to allow for the commute in order to have a 95%
probability of arriving at work on time.
3
How do we solve this?

4. Non Probabilistic
• Point estimate – one value as the
‘best guess’ for the population
parameter
• E.g. Sample mean is a point
estimate for Population mean
4
Approach to Uncertainty
Probabilistic
• Interval estimate – Range of
values that is likely to contain the
population parameter
• E.g. Sample mean lies within [a.b]
with 95% confidence (i.e. a
confidence interval)
Sample Population
Statistic Parameter

5.  Scenario Analysis
• Best case, most likely, worst case
• Multiple scenarios
• Discrete outcomes
 Decision tree
• Discrete outcomes
• Sequential decisions
 Monte Carlo Simulation
• Combines both scenario analysis and decision trees
• Continuous outcomes
5
Three types of probabilistic approach

6. 6
What is Monte Carlo Simulation?
X
Y
Z
A
Functional relationship (f) + Random sampling
(1) Input Distributional
Assumptions
(2) (3)
(4) Output
distribution
Uncertainty in
model inputs
Uncertainty in
model outputs

7. 7
Avoid becoming a Turkey
Source: http://www.mymoneyblog.com/talebs-thanksgiving-
turkey.html
Source: http://nassimtaleb.org/2013/09/turkey-problem/#.
VFHb1FfGWM8
Absence of evidence is not evidence of absence

8. 8
The power of Simulation
The biggest power of Simulation is to draw a distribution that mimics the actual real life data
generating process. Once an analyst can get hold of such a distribution, the sky is the limit to
how she/he wants to dissect the data
Source: Google Images
Question: Can we give a range for the minutes its takes to get to office associated
with the 100% confidence interval?

9. 9
Origin
Stanislaw Ulam
Source: takegame.com Source: en.wikipedia.org
“…….The question was what are the chances that a Canfield solitaire laid out with 52
cards will come out successfully? After spending a lot of time trying to estimate
them by pure combinatorial calculations, I wondered whether a more practical
method than ‘abstract thinking’ might not be to lay it out say one hundred times and
simply observe and count the number of successful plays…..”
-Eckhardt, Roger (1987). Stan Ulam, John von Neumann, and the Monte Carlo method, Los Alamos Science

10. 10
Analog Computation of Monte Carlo
Enrico Fermi, Italian physicist
Source:
http://en.wikipedia.org/wiki/FERMIAC
The Monte Carlo trolley, or FERMIAC, was an analog
computer invented by physicist Enrico Fermi to aid in
his studies of neutron transport.
Source: http://en.wikipedia.org/wiki/FERMIAC
Source: en.wikipedia.org

11. First Electronic Computation of Monte Carlo
John Von Neumann, Stanislaw Ulam, and
Nicholas Metropolis were part of the
Manhattan project during World War II.
Source: lanl.gov
The Manhattan Project
ENIAC, the first electronic general purpose computer.
Source: en.wikipedia.org
Solving the chain reaction in highly enriched uranium was too complex with algebraic equations.
Hence, simulations were used - plugging many different numbers into the equations and calculating
the result. Systematically plugging in and trying numbers would have taken too long. So they created
a new approach -- plugging in randomly chosen numbers into the equations and calculating the
results.

12. Impediments
• Estimating distributions of input variables
– It is far easier to estimate an expected growth rate of 8% in revenues for the next
5 years than it is to specify the distribution of expected growth rates – the type of
distribution, parameters of that distribution.
• Simulation can be time and resource intensive
12
Simulation: Keep in mind
Benefits
• Simulation gives a way out when stuck against a complicated intractable
mathematical dilemma
• Output is a distribution rather than a point estimate
– Investment with a higher expected return may have a fat tailed distribution
Pitfalls
• Garbage in, garbage out: For simulations to have value, the distributions should be
based upon analysis and data, rather than guesswork
• Benefits that decision-makers get by having a fuller picture of the uncertainty may be
more than offset by misuse of simulation

13. 13
When to use Simulation?
It is appropriate to use MC simulation
when:
• It is impossible or too expensive to
obtain data
• The observed system is too complex
• The analytical solution is difficult to
obtain
• It is impossible or too costly to
validate the mathematical
experiment
Probability of any number on an unbiased
die is = (no. of favorable outcomes)/(total
number of outcomes)
You can also throw the die 1000 times and
note the outcome
-Rubinstein (1976)
Source: psdgraphics.com

14. • VaR for a single asset
– Assume normality
– Mean of Rs 120 lakhs and an annual standard deviation of Rs 10 lakhs
– With 95% confidence, you can say that the value of this asset will not drop below
Rs 100 lakhs (two standard deviations below from the mean) or rise above Rs
140 lakhs (two standard deviations above the mean) over the next year.
14
Risk for a single asset
Source: Google Images

15. 15
Risk for a portfolio of assets
• VaR for a portfolio of assets
o Assume normality
o Portfolio consists of 10 individual assets with mean value varying from INR
50 lakhs to INR 950 lakhs
o Standard deviation varies from INR 5 lakh to INR 100 lakh

16. 16
Evaluating risk in a Fund Structure
Bond 1
Costs
Interest Received
Investor Payouts
Repayments
Reinvestments
Bond 2
Bond 3
Bond 10
Structure
P(d))
Investor Return
P(d))
P(d))
P(d))

17. • One of the earliest known methodology introduced in 1996
• This method creates a hypothetical portfolio of uncorrelated and homogenous assets
from the original asset pool.
17
Moody’s Binomial Expansion Technique
Statistic Description
Step 1:
Diversity Score (DS)
Reduction of the heterogeneous asset pool into homogeneous and independent
assets. The higher the concentration of assets in the underlying pool, the lower
the DS
Step 2:
Cash flow computations
Generating cash flows for combinations of each possible homogenous bonds
defaulting
Step 3:
Tranche cash flows
Putting the cash flows generated in Step 2 through the tranche waterfall to check
for losses. In this step, other variables, like interest rates, can also be changed to
account for different scenarios
Step 4:
Determine default probability
The default probability is determined based on output from Step 3 and after
taking into consideration the tenure and rating
Step 5:
Deriving the loss distribution
curve
Based on the different scenarios in Step 3 and the default probabilities
calculated in Step 4 for each scenario, the loss distribution curve is derived
Step 6:
Comparing loss distribution
The loss distribution in Step 5 is compared to a target loss distribution for a
tranche to see if the credit enhancement is adequate for the sought rating

18. 18
Moody’s Binomial Expansion Technique
Original Asset
Pool
Homogenous
and
Uncorrelated
Hypothetical
Asset Pool
Diversity Score –
No. of Assets
ND D D D
D ND D D
D D ND D
D D D ND
Present Value of
Cash flows for each
scenario
Probability of each
cash flow obtained
using binomial
formula
Expected Loss Curve
Expected loss curve
compared to benchmark
expected loss curve for the
sought rating

19. • Restrictive assumptions
• Useful only when the size of holdings and default probability distributions are
homogenous in the collateral pool.
• The correlation factor is reduced to zero in the constructed hypothetical portfolio.
• BET fails the accuracy test when DS is less than the total number of assets in the
original pool, which will be an almost always case due to the presence of contagion
effects and correlation in the larger asset pool.
• Inverse relationship between correlation and DS
Moody’s had dealt with this issue by upward adjustment of the calculated portfolio default
rates based on the WAR of the pool . Such an approach is open to criticisms of ad hoc
adjustments to the model.
19
Criticisms

20. • It is impossible or too expensive to obtain data
• The observed system is too complex
• The analytical solution is difficult to obtain
• It is impossible or too costly to validate the mathematical experiment
Thus, based on Rubinstein’s four criteria, the use of MC simulations for CDO rating is
justified.
20
Can we use Simulation instead?

21. 21
S&P’s Simulation Approach to Rating
*For methodology sanctity, the model assumptions used in both Step 1 and Step 2 should be the same,
else the SDRs obtained from Step 1 cannot be compared to BEDRs obtained from Step 2
** Scenario Default Rates *** Break-Even Default Rates

22. 22
S&P’s Simulation Approach to Rating
S&P’s simulation approach to rating is the dominant method for rating CDOs
Two step process,
• In the first step, an expected loss distribution for the underlying assets is estimated.
• In the second step, cash flow simulations are conducted to check if a particular
tranche can withstand the required level of defaults for a given rating.
Generating the expected loss distribution
• Estimated using MC simulations based on the historical observed CDR for the
underlying rated assets.
• Correlation assumptions are made
Two statistics are computed by S&P – the ‘scenario default rate’ (SDR) and the
‘breakeven default rate’ (BEDR)
• SDR - The extent of default in the underlying asset pool that a tranche must be
able to withstand to secure the sought rating
• BEDR indicates the actual level of default in the underlying asset pool which a
tranche sustains

23. 23
The Scenario Default Rate
12%
10%
8%
6%
4%
2%
0%
SDR (AA) = 37%,
CDR = 0.51%
1%
3%
5%
7%
9%
11%
13%
15%
17%
19%
21%
23%
25%
27%
29%
31%
33%
35%
37%
39%
41%
43%
45%
47%
Probability
Default rates in the underlying portfolio
SDR (AAA) = 43%,
CDR=0.15%
If the expected default rate of a10-year AAA-rated corporate bond is 0.15%, the SDR for the
tranche (which aspires to be rated AAA) is set equal to the level of default in the CDO’s collateral
pool that has no greater than 0.15% chance of being exceeded. The logic is ‘‘if the tranche can
survive defaults up to the SDR then its probability of default is no greater than 0.15%, as would
be appropriate for an AAA rating’’ (Global Cash Flow and Synthetic CDO Criteria, p.42).

24. 24
Consolidated Approach
*Model assumptions are coded in the consolidated model to ensure uniformity of structure across the
cash flow model and the CDO model.

25. 25
The difference is the use of historical default rates
http://www.standardandpoors.com/ratings/articles/en/us/?articleType=HTML&assetID=1245331158575

26.  Built the consolidated cash flow model
 Randomize variables like default flags, default amount, time of default,
prepayments, recovery.
o Unlike scenario analysis and decision trees, there is no constraint on how many
variables can be allowed to vary in a simulation
o Be careful specifying the probability distributions for each variable
 Sample randomly from the defined distributions and run the inputs past the
cash flow model to get the payouts
 For each trial, run the payouts against the waterfall and record if the cash flows
were sufficient to meet each tranche commitment or not
 Compare the default instances with the historical default studies to impute
rating
26
Steps of MC Simulations
Source: CRISIL Default Study, 2012

27. What is at stake?
27
Conversion of low rated underlying pool assets into high rated tranches in the US
subprime crisis highlights the need for better understanding
Source: Efraim Benmelech, Jennifer Dlugosz, 2009, The Alchemy of CDO Ratings, NBER
Working Paper Series 14878

28. 28
Thank you