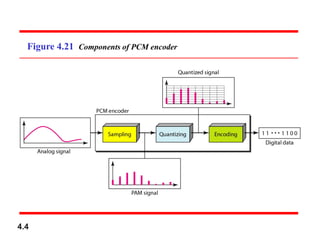
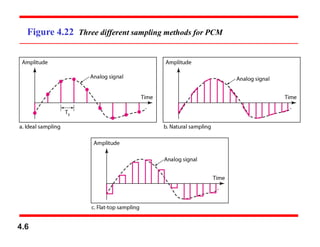
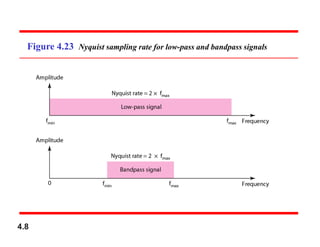
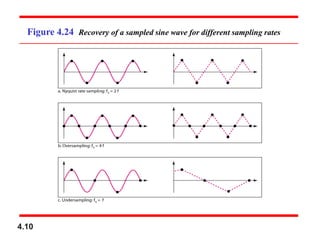
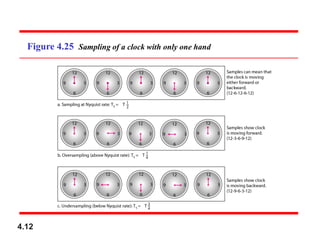
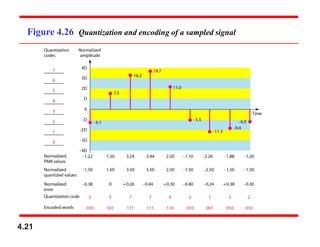
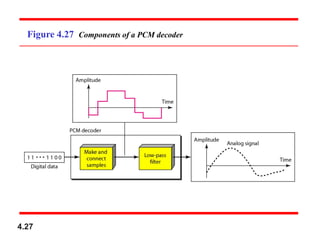
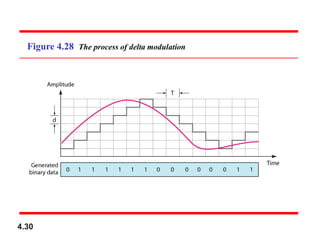
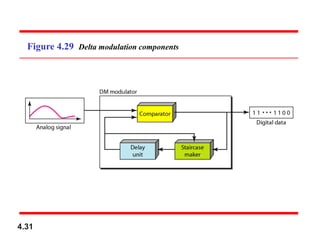
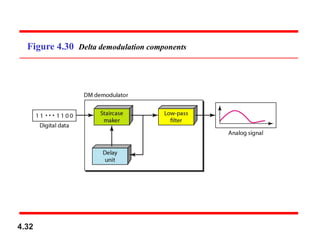
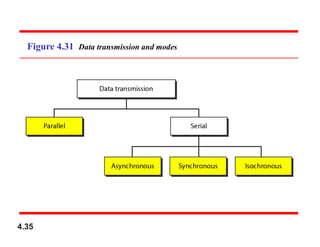
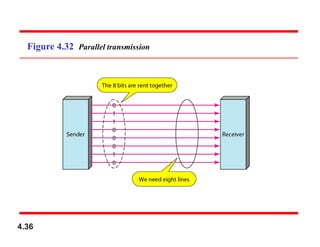
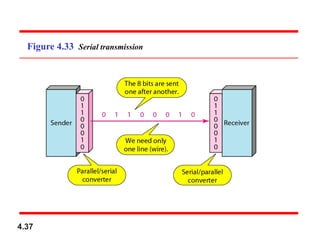
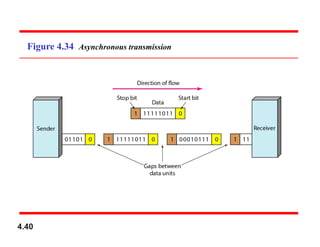
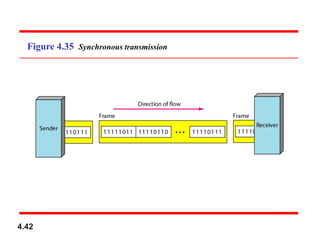
Chapter 4 covers data communication and networking, focusing on digital transmission and the conversion of analog signals to digital signals, emphasizing the robustness of digital signals against noise. It details pulse code modulation (PCM) and delta modulation (DM) as techniques for digitizing analog signals, including sampling, quantization, and binary encoding processes. Additionally, it explains transmission modes, including parallel and serial, with subcategories such as asynchronous, synchronous, and isochronous transmission.