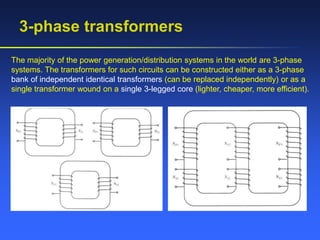
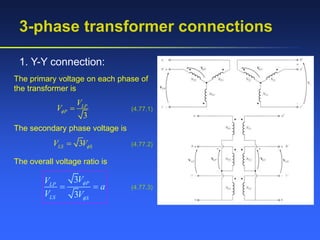
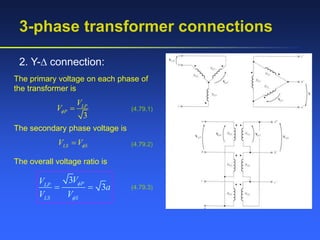
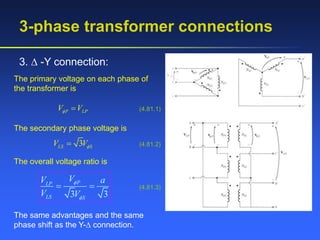
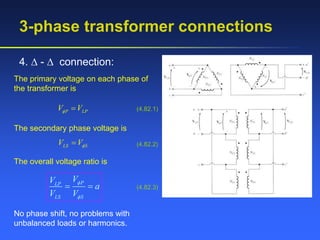
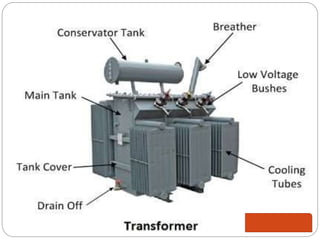
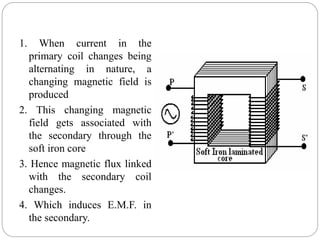
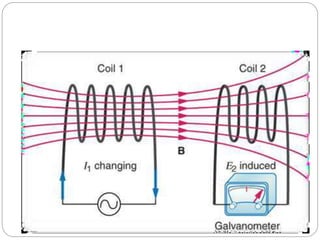
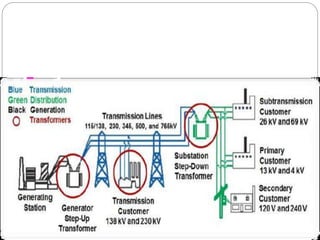
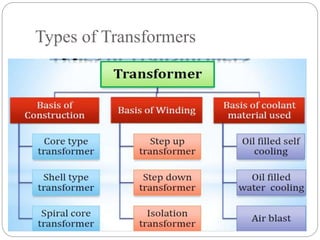
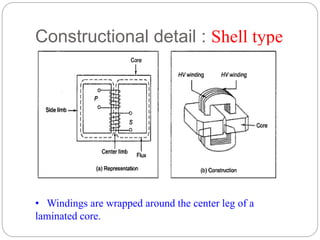
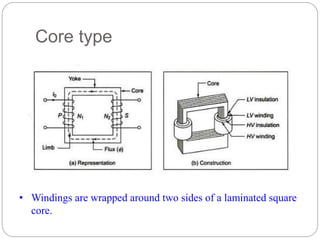
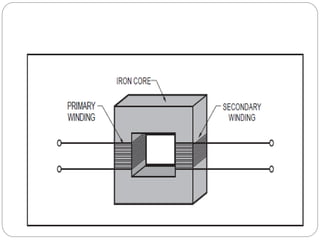
This document provides an overview of transformers, including: - The basic components and working principle of transformers based on electromagnetic induction. - The need for transformers to adjust voltages for transmission and household use by stepping up or down voltages. - Types of transformer construction including shell and core types. - Key factors that affect transformer performance like core material properties, turns ratio, and equations for ideal transformer voltage and current ratios. 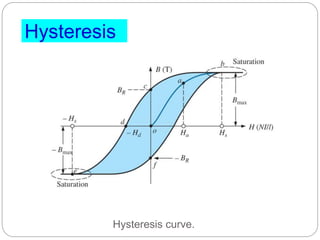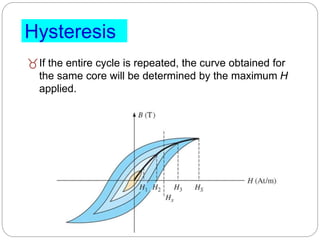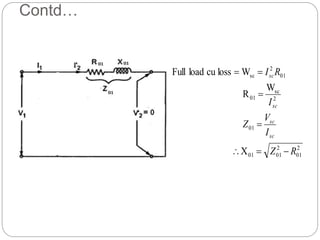- Sources of transformer losses and factors considered in transformer design like core material selection and lamination to reduce losses.

1. By-Nishant Kumar
Assistant Professor
TRANSFORMERS

2. “ Transformers are the heart of the
alternating current system.”
- William Stanley Jr.

3. Contents
 Introduction
 Need of transformer
 Working principle
 Construction
 Types of Transformers
 Magnetic Materials
 B-H Characteristics
 Ideal And Practical Transformer
 EMF Equation of Transformer
 Equivalent Circuit of Transformer
 Losses In Transformers
 Regulation And Efficiency
 Auto-transformer
 Three-phase Transformer Connections

4. Introduction
 Transformer is a static device.
 It transfer electrical energy from one part
of the electrical or electronic circuit to
other part of circuit without changing the
frequency.
 It works on the Michal Faradays law of
Electromagnetic Mutual Induction.

5. Symbol of Transformer

6. Need of Transformer
 In most cases, appliances are manufactured to work under
some specific voltages. Transformers are used to adjust the
voltages to a proper level.
 The transformers are the basic components for the
transmission of the electricity.
 Transformer is used to increase the voltage at the power
generating station(Step up) and used to decrease the
voltage(Step down) for house hold purpose.
 By increasing the voltages the loss of the electricity in the
transmission purpose is minimized.

8. Working principle of Transformer
 It works on the principle of Electromagnetic Mutual
Induction.
 Electromagnetic Mutual Induction:
When the current is provided to the Primary Winding it
behaves as electromagnet due to this the EMF is induced in
the Secondary winding as it comes in the area having
magnetic field lines due to primary Winding.
Vs = Ns.dΦ/dt
Vs = Secondary Winding Voltage
Ns = Secondary Winding Turns .

9. 1. When current in the
primary coil changes being
alternating in nature, a
changing magnetic field is
produced
2. This changing magnetic
field gets associated with
the secondary through the
soft iron core
3. Hence magnetic flux linked
with the secondary coil
changes.
4. Which induces E.M.F. in
the secondary.

11. Construction

12. Parts of a Transformer
A transformer consists of 3 basic components
 Primary Coil or Primary Winding : It is an
electrical wire wrapped around the core on the
input side
 Secondary Coil or Secondary Winding: It is an
electrical wire wrapped around the core on the
output side
 Core : A ferromagnetic material that can conduct a
magnetic field through it. Example: Iron

14. Types of Transformers

16. Constructional detail : Shell type
• Windings are wrapped around the center leg of a
laminated core.

17. Core type
• Windings are wrapped around two sides of a laminated square
core.

21. Permeability
Another factor affecting the field strength is
the type of core used.
If cores of different materials with the same
physical dimensions are used in the
electromagnet, the strength of the magnet will
vary in accordance with the core used.
The variation in strength is due to the number
of flux lines passing through the core.
Magnetic Materials

22. Magnetic material is material in which flux
lines can readily be created and is said to
have high permeability.
Permeability () is a measure of the ease
with which magnetic flux lines can be
established in the material.

23. Permeability of free space 0 (vacuum) is
Materials that have permeability slightly
less than that of free space are said to be
diamagnetic and those with permeability
slightly greater than that of free space are
said to be paramagnetic.
 
Wb/A.m
10
4 7


 
o

24. Magnetic materials, such as iron, nickel,
steel and alloys of these materials, have
permeability hundreds and even thousands
of times that of free space and are referred
to as ferromagnetic.
The ratio of the permeability of a material to
that of free space is called relative
permeability:
o
r


 

25. In general for ferromagnetic materials,
For nonmagnetic materials,
Relative permeability is a function of
operating conditions.
100

r

1

r


26. The entire curve (shaded) is called the
hysteresis curve.
 The flux density B lagged behind the
magnetizing force H during the entire plotting
of the curve. When H was zero at c, B was
not zero but had only begun to decline. Long
after H had passed through zero and had
equaled to –Hd did the flux density B finally
become equal to zero
B-H Characteristics

27. Hysteresis curve.
Hysteresis

28. If the entire cycle is repeated, the curve obtained for
the same core will be determined by the maximum H
applied.
Hysteresis

29. Normal magnetization curve for
three ferromagnetic materials.
Hysteresis

30. Transformer Core Material
Features of silicon steel:
1. Ferromagnetic material –this has superior magnetic
properties.
2. High permeability(µ) and low reluctance to flow of flux.
3. Low hysteresis coefficient.
Wh = η * Bmax
n * f * V
n = Steinmetz exponent, ranges from 1.5 to 2.5, depending on
material
n= 1.65 for silicon steel, lower side of range.
If value of n is less , then hysteresis loss will be less.

31. 4. Pure steel is good magnetic material but has high
conductivity. EMF’s are induced in core due to
conductivity of pure steel .these EMF’s produces
circulating currents in the core which produce eddy current
losses.
5.To reduce eddy current loss, reduce the conductivity of steel
without disturbing permeability of steel.
6.Brittleness of core increases if silica content of steel is
increases.
7.(4-5)% of silicon has to steel, so that conductivity of steel
decreases. Conductivity decreases, then eddy current loss
decreases.
8.Lamination technique is still used to further reduce
conductivity of steel, so that eddy current losses are
reduced.

32. CRGO steel
 The direction of magnetization in all the grains of this CRGO
steel material is along the edges, therefore overall
permeability of silicon steel will be increased. This process is
called “cold rolling grain orientation”(CRGO Steel) process.
µ (CRGO Steel)> µ (silicon Steel)
As permeability is increases, less excitation current is required
to produce flux.
To get same amount of flux, the silicon steel with more cross
sectional area is required as compared with CRGO Steel

33. Ideal and Practical Transformer
 An ideal transformer is a transformer which has no loses,
i.e. it’s winding has no ohmic resistance, no magnetic
leakage, and therefore no power and core loses.
 However, it is impossible to realize such a transformer in
practice.
 Yet, the approximate characteristic of ideal transformer
will be used in characterized the practical transformer.

34. Ideal Transformers
 Zero leakage flux:
-Fluxes produced by the primary and secondary currents
are confined within the core
 The windings have no resistance:
- Induced voltages equal applied voltages
 The core has infinite permeability
- Reluctance of the core is zero
- Negligible current is required to establish magnetic
flux
 Loss-less magnetic core
- No hysteresis or eddy currents

35. EMF Equation of Transformer

37. Form factor =r.m.s. value/ avg. value = 1.11
∴ r.m.s. value of e.m.f./turn = 1.11 × 4 f Φm
= 4.44 f Φm volt
Now, r.m.s.value of the induced e.m.f. in the whole of
primary winding = (induced e.m.f/turn) × No. of
primary turns
E1 = 4.44 f N1 Φm = 4.44 f N1 BmA.........(1)
Similarly, r.m.s. value of the e.m.f. induced in secondary
is, E2 = 4.44 f N2 Φm = 4.44 f N2 BmA..........(2)
Equation 1,2 represents the e.m.f equation.

38. Ideal transformer
V1 – supply voltage ; I1- noload input current ;
V2- output voltgae; I2- output current
Im- magnetising current;
E1-self induced emf ; E2- mutually induced emf

39. Continued…
 This is called the emf equation of transformer, which shows,
emf / number of turns is same for both primary and secondary
winding.
For an ideal transformer on no load, E1 = V1 and E2 = V2 .
where, V1 = supply voltage of primary winding
V2 = terminal voltage of secondary winding
 Factors affecting the induced emf are:
1. Flux Φm
2. Frequency of applied voltage
3. Number of turns N.

40. Continued…
 Voltage ratios of the transformer with load:
 As shown in fig.(1), let
N1 = Number of turns in primary winding
N2 = Number of turns in secondary winding
E1 = rms induced voltage in primary winding
E2 = rms induced voltage in secondary winding
E1 = 4.44f N1 Φm volts
E2 = 4.44f N2 Φm volts
By taking the ratio of these expressions we get,
E1 …(1)
N2
=
N1
E2

41. Continued…
 Voltage ratios of the transformer without load:
 Assume the load on secondary winding is disconnected.
∴ I2 = 0
∴ load terminal voltage v2 is equal to secondary induced
voltage E2
i.e. V2 = E2 …….(2)
 As the primary current on no load is very small,
V1 = E1 …….(3)
By substituting eq.(2) & (3) in eq.(1) we get,
V1 N1 ……(4)
V2
=
N2

42. Continued…
 Turns ratio:
The turns ratio of a transformer is defined as the ratio
of the number of primary turns to the number of secondary
turns.
∴ turns ratio = N1 …….(6)
 Types of transformers based on the value of K:
1. Step up transformer:
If K > 1 or V2 > V1 is called step up transformer.
2. Step down transformer:
If K < 1 or V2 < V1 is called step down transformer.
N2

43. Continued…
3. One-to-one transformer:
If K=1 or V1 = V2 is called as a one-to-one transformer. It
is also known as the isolation transformer.
 Current ratios:
 The transformer transfer electrical power from one side to the
other (primary to secondary) with a very high efficiency (η).
 If we assume that the power loss taking place in the transformer
is very low (η = 100%) then, we can write that
power input = power output
∴ V1 I1 cos ø1 = V2 I2 cos ø2 …….(7)
where I1 and I2 are the RMS values of the primary and secondary
currents of the transformer respectively.

44. Problems
1. A transformer has a primary voltage of 230v and
turns ratio of 5:1. Calculate the secondary
voltage
2. A transformer has 200 turns in the primary, 50
turns in the secondary, and 120 volts applied to
the primary (Vp). What is the voltage across the
secondary (V s)?

45. More Problems….
1. There are 400 turns of wire in an iron-core coil.
If this coil is to be used as the primary of a
transformer, how many turns must be wound on
the coil to form the secondary winding of the
transformer to have a secondary voltage of one
volt if the primary voltage is five volts?
2. A 12 volts transformer has 20 turns in the
primary, 5 turns in the secondary. What is the
voltage across the primary side (VP)?

46. Continued…
cos ø1 and cos ø2 are the power factors of the
primary and secondary sides of the transformer.
Practically they are of same value.
∴ cos ø1 = cos ø2 …..(8)
∴ V1 I1 = V2 I2 …..(9)
∴ I1 V2 N2 …..(10)
This expression shows that the primary &
secondary currents are inversely proportional to
the number of turns of the corresponding
windings.
=
I2 V1
= N1

47. Continued…
 As the voltage and current may or may not be in phase,
the units of transformer rating are Volt Ampere (VA)
or kiloVolt-Ampere (kVA) or Mega Volt Ampere
(MVA).
∴ Rating in VA or kVA or MVA = V1 x I1 = V2 x I2
 Why is the transformer rated I VA or kVA?
 There are two type of losses in a transformer;
1. Copper Losses
2. Iron Losses or Core Losses or Insulation Losses
 Copper losses ( I²R)depends on Current which passing
through transformer winding while Iron Losses or Core
Losses or Insulation Losses depends on Voltage.

48. Continued…
 Hence the total losses depends on the volt ampere (VA) and
not on the power factor. Therefore rating of transformer is
in VA or kVA and not in kW.
 The complete rating of a transformer:
 The complete rating of a transformer includes the ratio of
primary and secondary voltages, kVA rating and supply
frequencies as follows:
3300 V/ 240 V , 5 kVA , 50 Hz
where, 3300 V is primary voltage V1
240 V is secondary voltage V2
5 kVA is kVA rating and 50 Hz is the supply
frequency.

49. Continued…
 Specifications of transformer:
 When transformer is to be purchased, we have to
consider following specifications:
1. kVA rating 2. Number of phases
3. Primary voltage 4. Secondary voltage
5. Primary current 6. Secondary current
7. Frequency of operation
8. Types of cooling

50. Continued…
 table 1 shows the typical specifications of a
single phase transformer.
Sr.
No.
Specification/rating Value
1. kVA rating 5kVA
2. Number of phases 1
3. Primary voltage V1 230 V
4. Secondary voltage v2 100 V
5. Primary current I1 21 A
6. Secondary current I2 50 A
7. Frequency of operation 50 Hz
8. Cooling Open

51. Phasor diagram: Transformer on No-
load

52. Transformer on load assuming no
voltage drop in the winding
Fig shows the Phasor diagram of a transformer
on load by assuming
1. No voltage drop in the winding
2. Equal no. of primary and secondary turns

53. Transformer on load
Fig. a: Ideal transformer on load
Fig. b: Main flux and leakage
flux in a transformer

54. Phasor diagram of transformer with
UPF load

55. Phasor diagram of transformer with
lagging p.f load

56. Phasor diagram of transformer with
leading p.f load

57. Equivalent circuit of a transformer
No load equivalent circuit:

58. Equivalent circuit parameters referred to
primary and secondary sides respectively

59. Contd.,
 The effect of circuit parameters shouldn’t be changed
while transferring the parameters from one side to
another side
 It can be proved that a resistance of R2 in sec. is
equivalent to R2/k2 will be denoted as R2’(ie. Equivalent
sec. resistance w.r.t primary) which would have caused
the same loss as R2 in secondary,
2
2
2
2
1
2
'
2
2
2
2
'
2
2
1
k
R
R











R
I
I
R
I
R
I

60. Transferring secondary parameters
to primary side

61. Equivalent circuit referred to
secondary side
•Transferring primary side parameters to secondary side
Similarly exciting circuit parameters are also transferred to
secondary as Ro’ and Xo’

62. equivalent circuit w.r.t primary
where

63. Approximate equivalent circuit
 Since the noload current is 1% of the full load
current, the nolad circuit can be neglected

65. Transformer Tests
Electrical Machines
•The performance of a transformer can be calculated on the basis of
equivalent circuit
•The four main parameters of equivalent circuit are:
- R01 as referred to primary (or secondary R02)
- the equivalent leakage reactance X01 as referred to primary
(or secondary X02)
- Magnetising susceptance B0 ( or reactance X0)
- core loss conductance G0 (or resistance R0)
•The above constants can be easily determined by two tests
- Oper circuit test (O.C test / No load test)
- Short circuit test (S.C test/Impedance test)
•These tests are economical and convenient
- these tests furnish the result without actually loading the
transformer

66. In Open Circuit Test the transformer’s secondary winding is open-circuited, and
its primary winding is connected to a full-rated line voltage.
• Usually conducted on
H.V side
• To find
(i) No load loss or core
loss
(ii) No load current Io
which is helpful in
finding Go(or Ro ) and Bo
(or Xo )
2
0
2
0
0
2
0
oc
0
0
2
0
oc
0
0
o
0
0
0
2
2
0
0
0
m
0
0
w
c
0
0
0
0
0
0
B
e
susceptanc
Exciting
&
V
W
G
e
conductanc
Exciting
;
G
V
W
Y
;
Y
V
I
sin
I
I
cos
I
I
cos
cos
loss
Core
G
Y
V
I
-I
I
I
or
I
or
I
V
W
I
V
W
w
oc
oc



















Open-circuit Test
0
0
0
0
0
0
0
0
V
I
B
V
I
G
I
V
X
I
V
R
w
w







67. Short-circuit Test
In Short Circuit Test the secondary terminals are short circuited, and the
primary terminals are connected to a fairly low-voltage source
The input voltage is adjusted until the current in the short circuited windings
is equal to its rated value. The input voltage, current and power is
measured.
• Usually conducted on L.V side
• To find
(i) Full load copper loss – to pre determine the
efficiency
(ii) Z01 or Z02; X01 or X02; R01 or R02 - to predetermine the
voltage regulation

68. Contd…
2
01
2
01
01
01
2
sc
01
01
2
sc
X
W
R
W
loss
cu
load
Full
R
Z
I
V
Z
I
R
I
sc
sc
sc
sc








69. Transformer Voltage Regulation
and Efficiency
Electrical Machines
The output voltage of a transformer varies with the load even if the input
voltage remains constant. This is because a real transformer has series
impedance within it. Full load Voltage Regulation is a quantity that compares
the output voltage at no load with the output voltage at full load, defined by
this equation:
%
100
down
Regulation
%
100
up
Regulation
,
,
,
,
,
,






nl
S
fl
S
nl
S
fl
S
fl
S
nl
S
V
V
V
V
V
V  
 
%
100
/
down
Regulation
%
100
/
up
Regulation
V
V
k
noload
At
,
,
,
,
p
s
x
V
V
k
V
x
V
V
k
V
nl
S
fl
S
P
fl
S
fl
S
P





Ideal transformer, VR = 0%.

70. voltage
load
-
no
voltage
load
-
full
voltage
load
-
no
regulation
Voltage











1
2
1
2
N
N
V
V
p
s
p
s
N
N
V
V

recall
Secondary voltage on no-load
V2 is a secondary terminal voltage on full load


















1
2
1
2
1
2
1
regulation
Voltage
N
N
V
V
N
N
V
Substitute we have

71. Transformer Phasor Diagram
1/25/2024
71 Electrical Machines
 Aamir Hasan Khan
To determine the voltage regulation of a transformer, it is necessary
understand the voltage drops within it.

72. Transformer Phasor Diagram
1/25/2024
72 Electrical Machines
 Aamir Hasan Khan
Ignoring the excitation of the branch (since the current flow through the
branch is considered to be small), more consideration is given to the series
impedances (Req +jXeq).
Voltage Regulation depends on magnitude of the series impedance and the
phase angle of the current flowing through the transformer.
Phasor diagrams will determine the effects of these factors on the voltage
regulation. A phasor diagram consist of current and voltage vectors.
Assume that the reference phasor is the secondary voltage, VS. Therefore the
reference phasor will have 0 degrees in terms of angle.
Based upon the equivalent circuit, apply Kirchoff Voltage Law,
S
eq
S
eq
S
P
I
jX
I
R
V
k
V




73. Transformer Phasor Diagram
1/25/2024
73 Electrical Machines
 Aamir Hasan Khan
For lagging loads, VP / a > VS so the voltage regulation with lagging loads is > 0.
When the power factor is unity, VS is lower than VP so VR > 0.

74. Transformer Phasor Diagram
1/25/2024
74 Electrical Machines
 Aamir Hasan Khan
With a leading power factor, VS is higher than the referred VP so VR < 0

75. Transformer Phasor Diagram
Electrical Machines
For lagging loads, the vertical components of Req and Xeq will partially
cancel each other. Due to that, the angle of VP/a will be very small, hence
we can assume that VP/k is horizontal. Therefore the approximation will
be as follows:

76. 1/25/2024
Voltage regulation
Lagging P.F. VP/ k > VS V.R. > 0
Unity P.F. VP / k > VS V.R. >0
(smaller)
Leading P.F. VS > VP/ k V.R. < 0

77. Voltage regulation for Lagging Power Factor

78. Voltage Regulation for Leading Power
Factor

79. Formula: voltage regulation
leading
for
'-'
and
lagging
for
'
'
V
sin
cos
V
V
regulation
%
lues
primary va
of
In terms
leading
for
'-'
and
lagging
for
'
'
V
sin
cos
V
V
regulation
%
values
secondary
of
In terms
1
1
01
1
1
01
1
1
'
2
1
2
0
2
02
2
2
02
2
2
0
2
2
0










where
X
I
R
I
V
where
X
I
R
I
V





80. Transformer Efficiency
Electrical Machines
Transformer efficiency is defined as (applies to motors, generators and
transformers):
%
100


in
out
P
P

%
100



loss
out
out
P
P
P

Types of losses incurred in a transformer:
Copper I2R losses
Hysteresis losses
Eddy current losses
Therefore, for a transformer, efficiency may be calculated using the following:
%
100
cos
cos
x
I
V
P
P
I
V
S
S
core
Cu
S
S







81. Losses in a transformer
Core or Iron
loss:
Copper loss:

82. Condition for maximum efficiency

83. Contd.,
The load at which the two losses
are equal =

84.  Example:
 A 15kVA, 2300/230 V transformer tested to determine
1- its excitation branch components, 2- its series
impedances, and 3- its voltage regulation
 Following data taken from the primary side of the transformer:
Open Circuit Test Short Circuit Test
VOC=2300 V VSC=47 V
IOC=0.21A ISC=6 A
POC= 50 W PSC= 160 W

85. (a) Find the equivalent circuit referred to H.V. side
(b) Find the equivalent circuit referred to L. V. side
(c) Calculate the full-load voltage regulation at 0.8 lagging PF,
1.0 PF, and at 0.8 leading PF
(d) Find the efficiency at full load with PF 0.8 lagging
SOLUTION:
Open circuit impedance angle is:
Excitation admittance is:

84
21
.
0
2300
50
cos
cos 1
1



 

OC
OC
OC
OC
I
V
P













 
0000908
.
0
0000095
.
0
84
10
13
.
9
84
2300
21
.
0
84 5
j
V
I
Y
OC
OC
E




86. Transformer Voltage Regulation and
Efficiency
 Impedance of excitation branch referred to primary:
 Short Circuit Impedance angle:
 Equivalent series Impedance:
Req=4.45 Ω, Xeq=6.45 Ω






k
X
k
R
M
C
11
0000908
.
0
1
105
0000095
.
0
1

4
.
55
6
47
160
cos
cos 1
1



 

SC
SC
SC
SC
I
V
P











45
.
6
45
.
4
4
.
55
833
.
7
4
.
55
6
47
j
I
V
Z SC
SC
SC
SE




87. Transformer Voltage Regulation and
Efficiency
 The equivalent circuits shown below:


88.  (b) To find eq. cct. Referred to L.V. side,
impedances divided by a²=NP/NS=10
RC=1050 Ω , XM=110 Ω
Req=0.0445 Ω , Xeq=0.0645 Ω
 (c) full load current on secondary side:
IS,rated=Srated/ VS,rated=15000/230 =65.2 A
To determine V.R., VP/ a is needed
VP/a = VS + Req IS + j Xeq IS , and:
IS=65.2/_-36.9◦ A , at PF=0.8 lagging

89. Transformer Voltage Regulation and
Efficiency
 Therefore:
VP / a =
V.R.=(234.85-230)/230 x 100 %=2.1 % for 0.8 lagging
 At PF=0.8 leading  IS=65.2/_36.9◦ A
VP / a =
V
j
j
j
j






4
.
0
85
.
234
62
.
1
84
.
234
36
.
3
52
.
2
74
.
1
32
.
2
230
1
.
53
21
.
4
9
.
36
9
.
2
0
230
9
.
36
2
.
65
0645
.
0
)
9
.
36
2
.
65
)(
0445
.
0
(
0
230
























V
j
j
j
j






27
.
1
85
.
229
10
.
5
8
.
229
36
.
3
52
.
2
74
.
1
32
.
2
230
9
.
126
21
.
4
9
.
36
9
.
2
0
230
9
.
36
2
.
65
0645
.
0
)
9
.
36
2
.
65
)(
0445
.
0
(
0
230






















90. Transformer Voltage Regulation and
Efficiency
 V.R. = (229.85-230)/230 x 100%= -0.062%
 At PF=1.0 , IS= 65.2 /_0◦ A
 VP/a=
 V.R. = (232.94-230)/230 x 100% = 1.28 % for PF=1
V
j
j
j







04
.
1
94
.
232
21
.
4
9
.
232
21
.
4
9
.
2
230
90
21
.
4
0
9
.
2
0
230
)
0
2
.
65
)(
0645
.
0
(
)
0
2
.
65
)(
0445
.
0
(
0
230



















91. Transformer Voltage Regulation and
Efficiency
 Example: Phasor Diagrams …

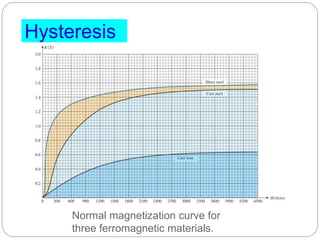
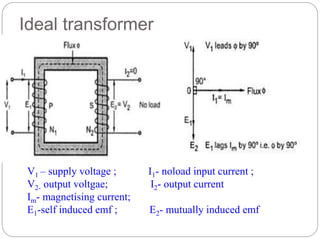
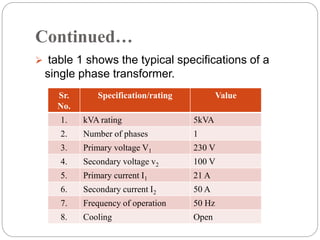
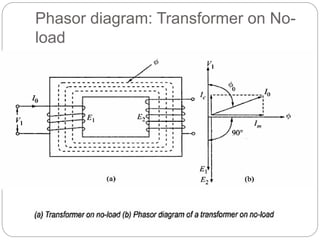
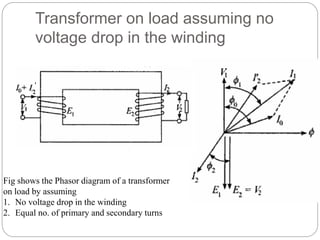
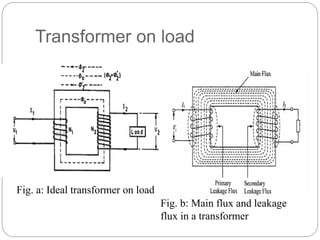
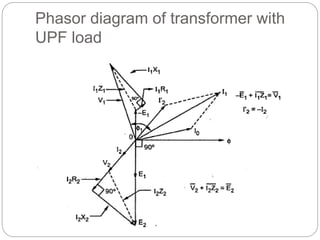
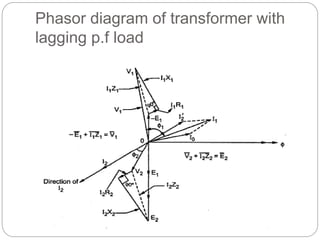
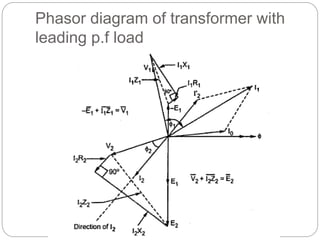
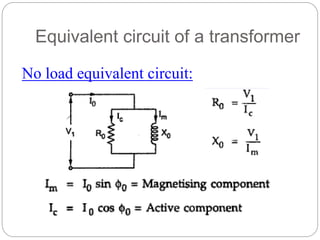
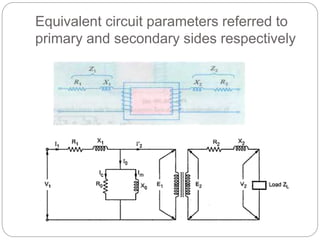
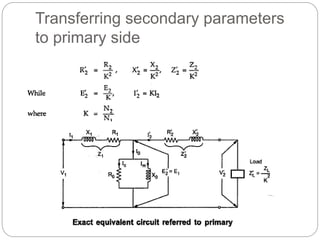
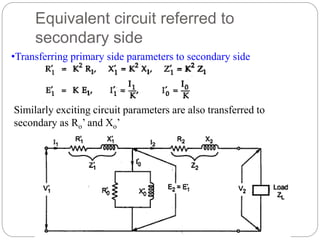
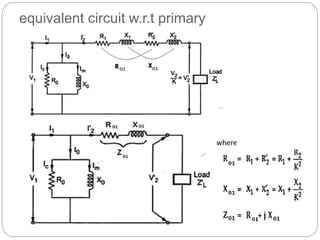
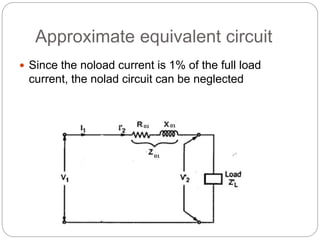
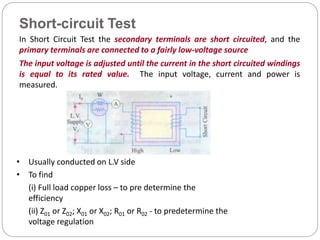
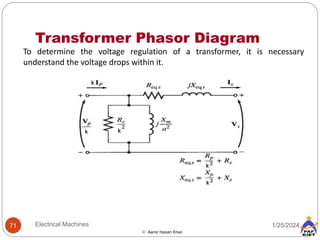
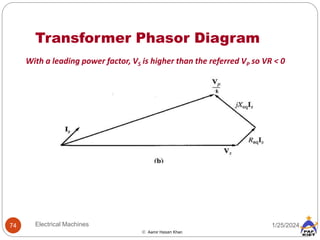
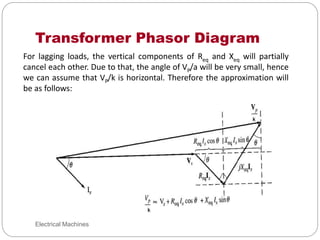
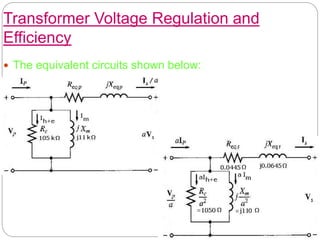
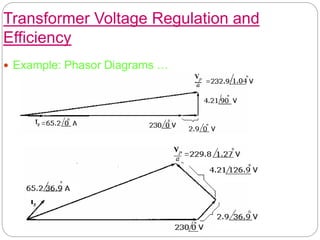
92. Transformer Voltage Regulation and
Efficiency
 (e) Efficiency of Transformer:
- Copper losses:
PCu=(IS)²Req =(65.2)² (0.0445)=189 W
- Core losses:
PCore= (VP/a)² / RC= (234.85)² / 1050=52.5 W
output power:
Pout=VSIS cosθ=230x65.2xcos36.9◦=12000 W
η= VSIS cosθ / [PCu+PCore+VSIS cosθ] x 100%=
12000/ [189+52.5+12000] = 98.03 %

93. All day efficiency
hours)
24
(
kWh
in
Input
kWh
in
output
in watts
input
in watts
put
out
efficiency
commercial
ordinary
day for
all 


•All day efficiency is always less than the commercial efficiency

97. 3-phase transformers
The majority of the power generation/distribution systems in the world are 3-phase
systems. The transformers for such circuits can be constructed either as a 3-phase
bank of independent identical transformers (can be replaced independently) or as a
single transformer wound on a single 3-legged core (lighter, cheaper, more efficient).

98. 3-phase transformer connections
We assume that any single transformer in a 3-phase transformer (bank)
behaves exactly as a single-phase transformer. The impedance, voltage
regulation, efficiency, and other calculations for 3-phase transformers are
done on a per-phase basis, using the techniques studied previously for
single-phase transformers.
Four possible connections for a 3-phase transformer bank are:
1. Y-Y
2. Y-
3. - 
4. -Y

99. 3-phase transformer connections
1. Y-Y connection:
The primary voltage on each phase of
the transformer is
3
LP
P
V
V  (4.77.1)
The secondary phase voltage is
3
LS S
V V
 (4.77.2)
The overall voltage ratio is
3
3
P
LP
LS S
V
V
a
V V


  (4.77.3)

100. 3-phase transformer connections
2. Y- connection:
The primary voltage on each phase of
the transformer is
3
LP
P
V
V  (4.79.1)
The secondary phase voltage is
LS S
V V
 (4.79.2)
The overall voltage ratio is
3
3
P
LP
LS S
V
V
a
V V


  (4.79.3)

101. 3-phase transformer connections
3.  -Y connection:
The primary voltage on each phase of
the transformer is
P LP
V V
  (4.81.1)
The secondary phase voltage is
3
LS S
V V
 (4.81.2)
The overall voltage ratio is
3 3
P
LP
LS S
V
V a
V V


  (4.81.3)
The same advantages and the same
phase shift as the Y- connection.

102. 3-phase transformer connections
4.  -  connection:
The primary voltage on each phase of
the transformer is
P LP
V V
  (4.82.1)
The secondary phase voltage is
LS S
V V
 (4.82.2)
The overall voltage ratio is
P
LP
LS S
V
V
a
V V


  (4.82.3)
No phase shift, no problems with
unbalanced loads or harmonics.