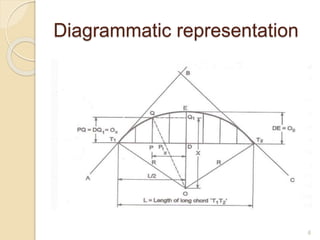
The document discusses the properties and characteristics of simple circular curves, including calculations for versed sine and apex distances using given parameters. It provides numerical problems that illustrate these concepts, showcasing example calculations for different scenarios. Additionally, it includes methods for setting out a circular curve based on chord offsets and offers diagrammatic representations.

1. Properties/Characteristics of
simple circular curve(contd…)
Versed Sine, DE
In the figure, DE = OE – OD = R - OD
In triangle T1DO, cos Ø/2 = OD / OT1 as
OT1 = radius (R). So, OD = R cos Ø/2
Hence, DE = R – R cos Ø/2
DE = R (1- cos Ø/2 )
Apex Distance, BE
In the figure, BE = OB – OE = OB – R
In triangle BT1O, cos Ø/2 = OT1 / OB or
OB = OT1 / cos Ø/2 = R sec Ø/2
Hence, BE = OB – R = R sec Ø/2 – R
BE = R (sec Ø/2 – 1)
1

2. Numerical problem 2
If two tangents intersect at a chainage of
1000 m at 109°such that the radius of the
curve is 130 m, calculate the versed sine
and apex distance of the curve.
Ans: Versed sine = 24.16 m
Apex distance = 29.68 m
2

3. Setting out a simple circular curve
by taking offsets from the long
chord
 Here P1 & other points on curve are
ordinates or offsets
PD = x ; PP1 = Ox ; DE = Oo (versed sine)
T1DT2 = Long chord ; BE is apex distance
BT1 or BT2 the tangent length
To set out the curve, the long chord is
divided into two equal halves such that
the curve is symmetrical about both the
halves.
In triangle OT1D,
3

4. 4

5. Numerical problem 3
 Calculate the ordinates at an interval of 6 m
for a simple circular curve whose long chord
is of 60 m and radius is 150 m.
Ans: Deflection angle = 23°
Tangent length = 30.52 m
Degree of curve = 11.4°
Length of curve = 60.21 m
Apex distance = 3.07 m
Versed sine = 3.01 m
Calculate O6, O12, O18, O24, O30
5

6. Diagrammatic representation
6