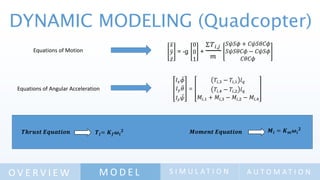
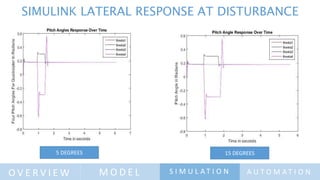
The document discusses the design and simulation of a multicopter's autonomy model, highlighting objectives such as conducting experiments, mathematical modeling, and programming the flight controller. It covers the methodology involving hover stability, linear motion, and dynamic modeling, along with the equations of motion and control laws for altitude and attitude. The conclusion emphasizes the significance of automation and successful simulation results in achieving stable multicopter performance.