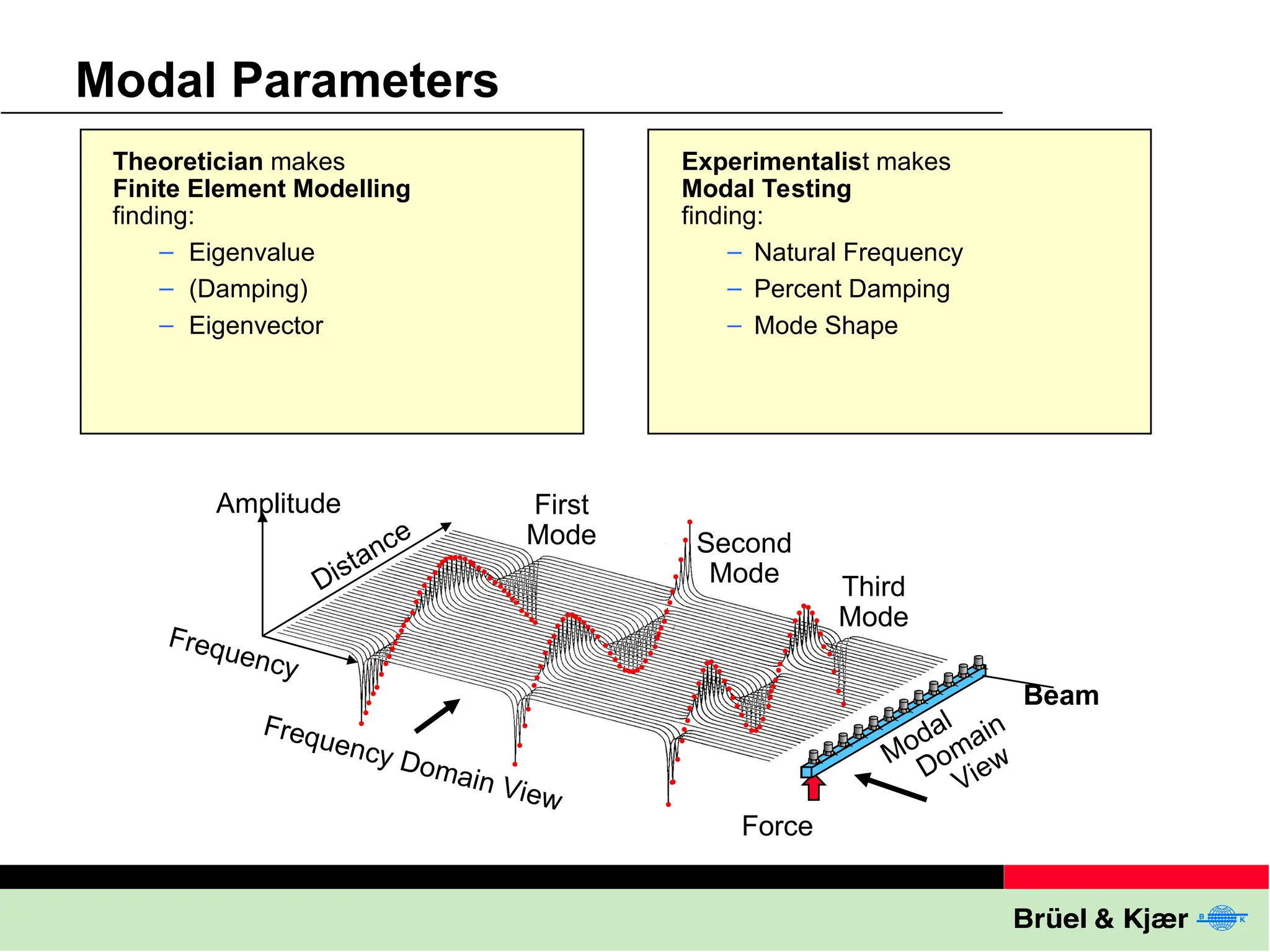
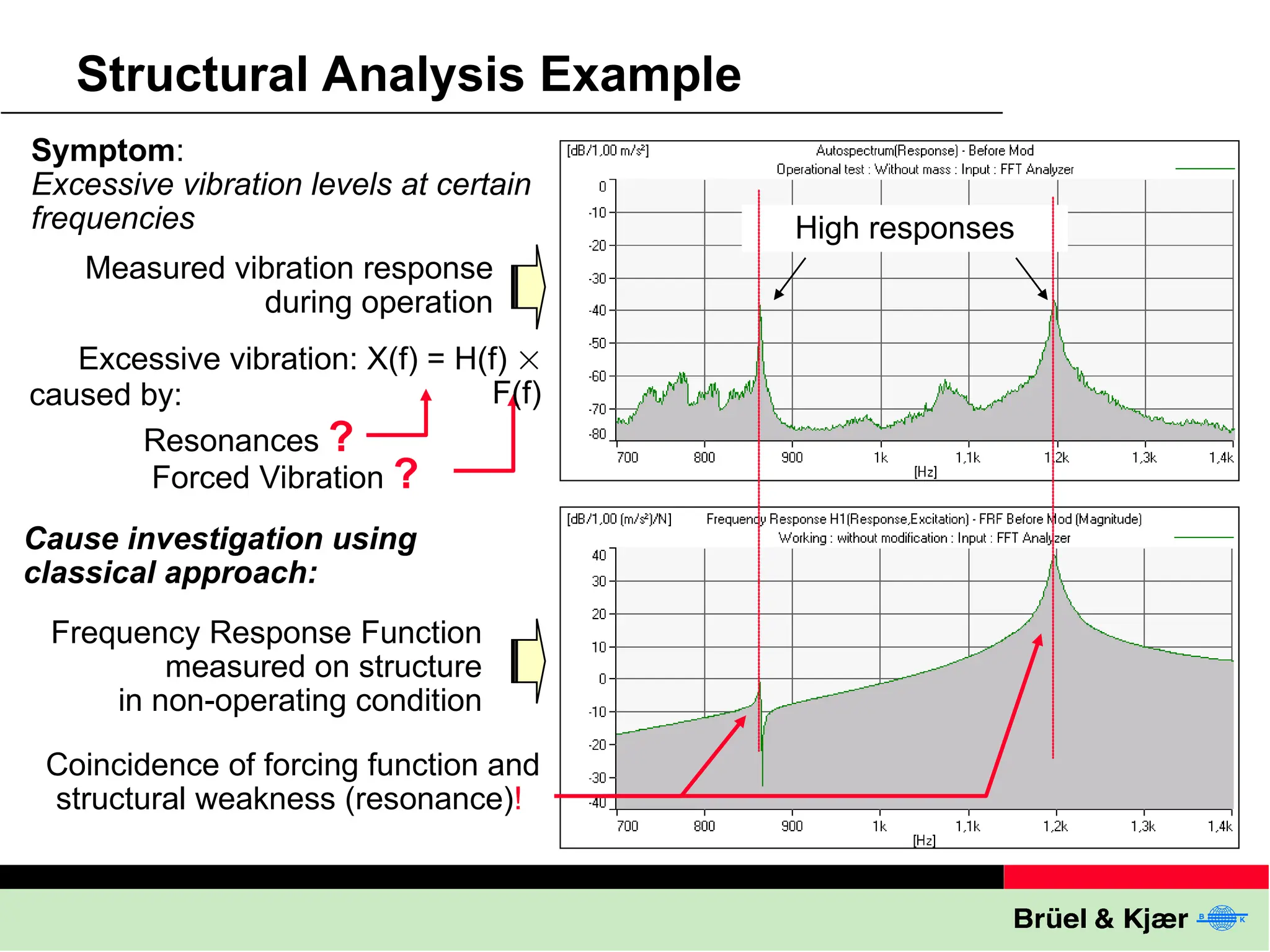
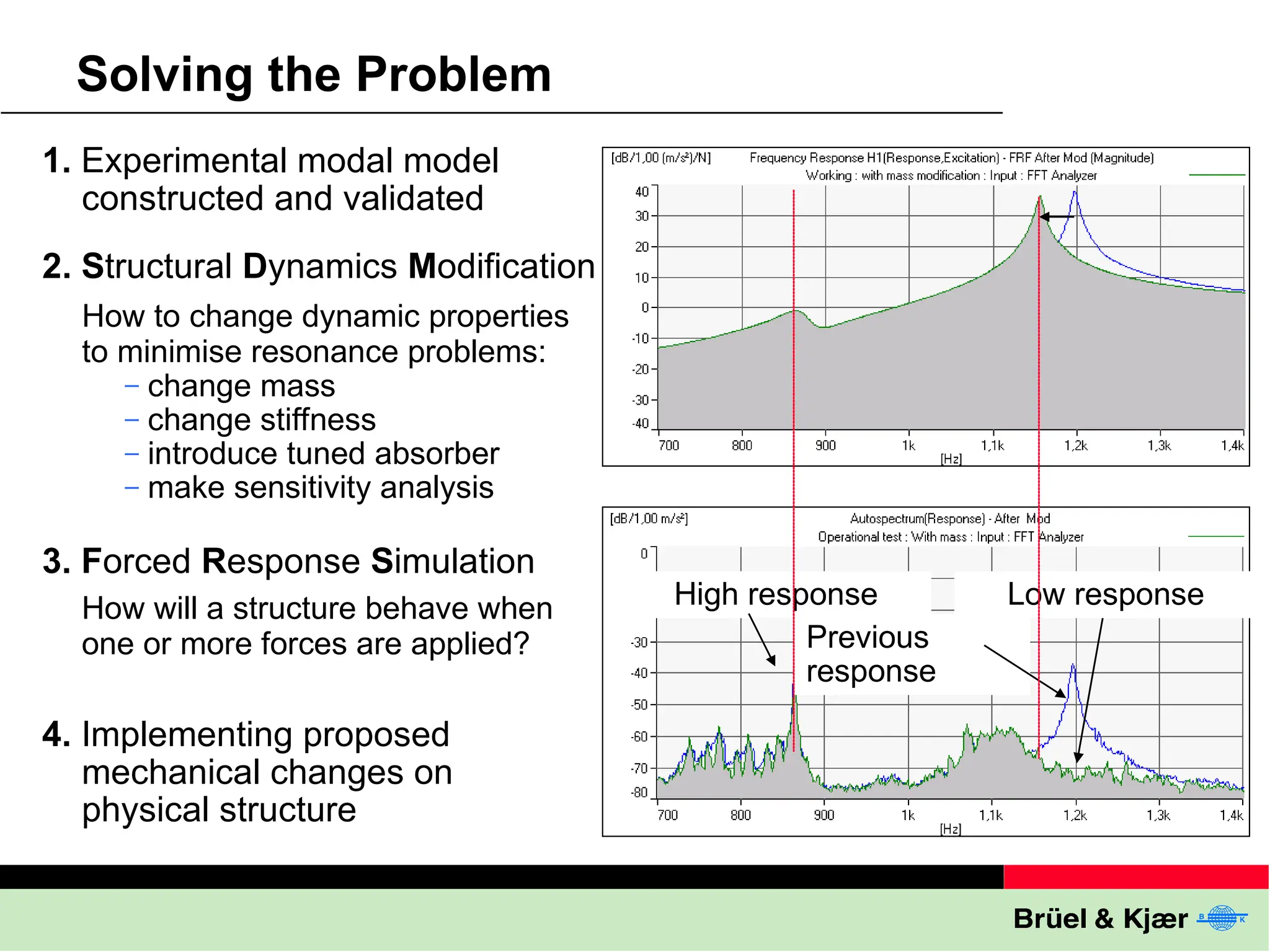
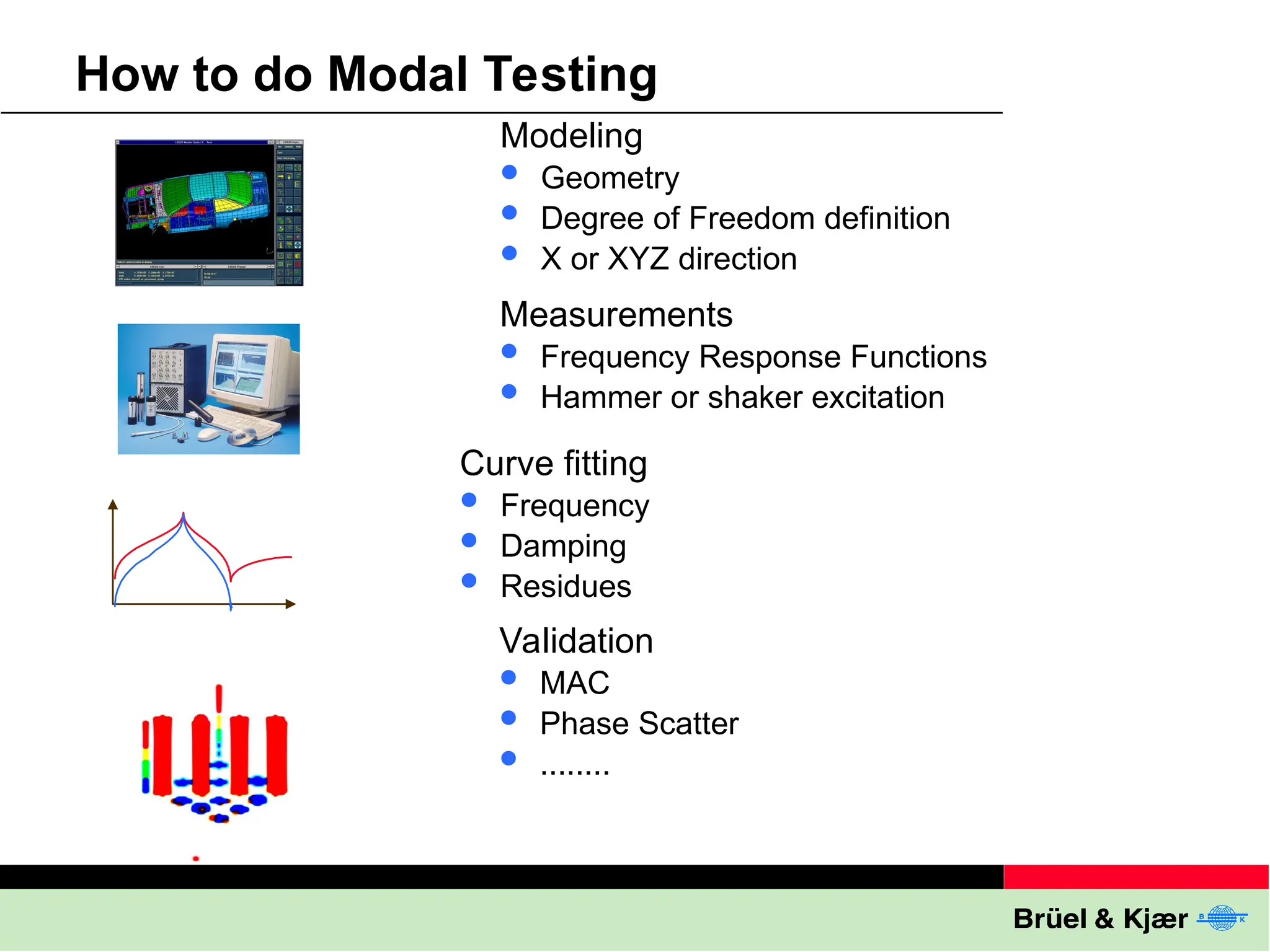
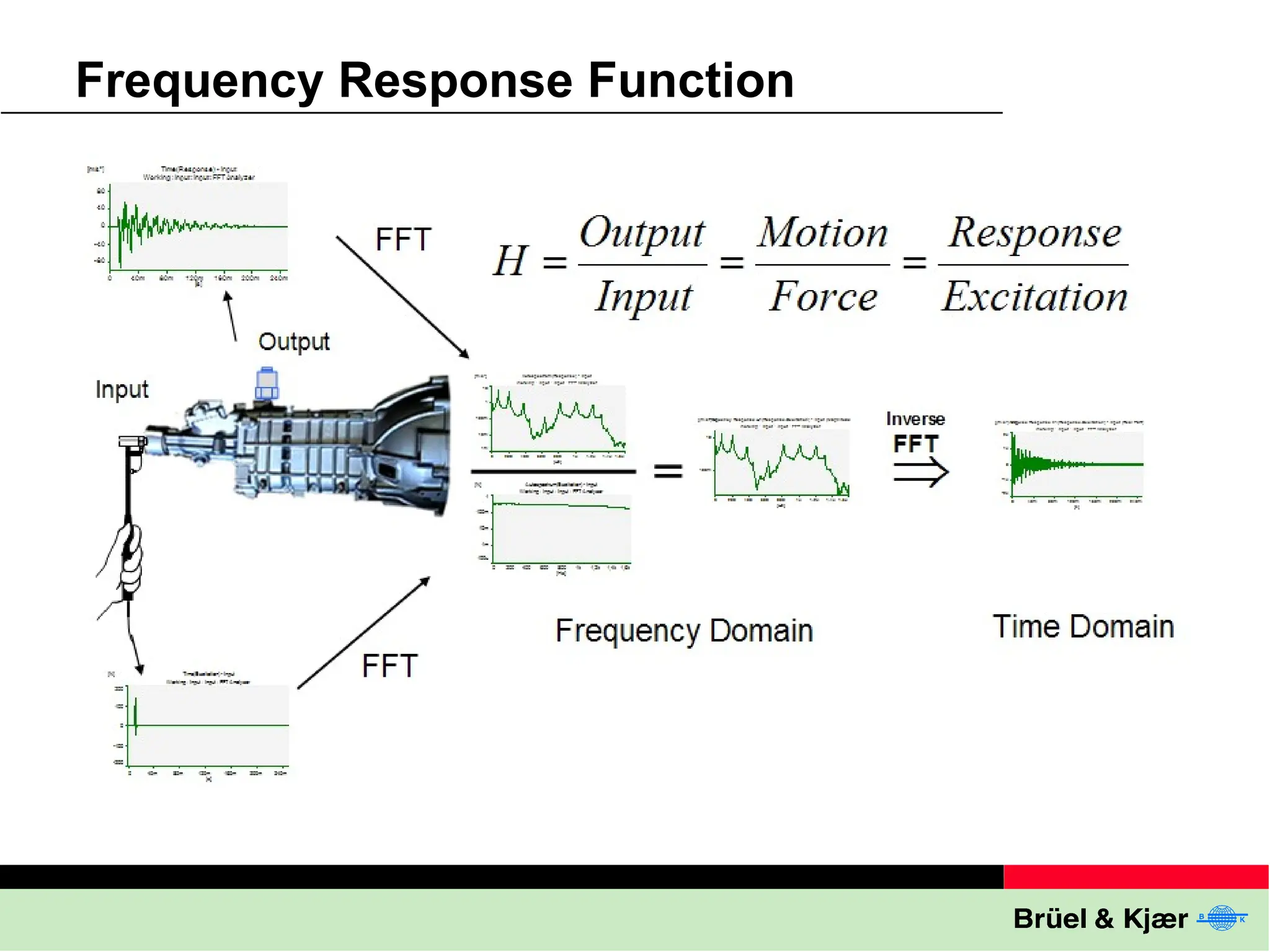
The document discusses the process and significance of modal testing, which involves constructing a mathematical model of a structure's vibrational behavior through experimental means. It highlights applications such as troubleshooting excessive vibration, validating finite element models, and predicting dynamic responses in various industries, including aerospace and automotive. The document also outlines methods and tools used in modal testing, like geometry definition and frequency response functions.