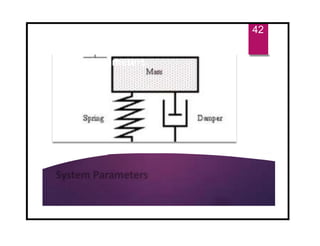
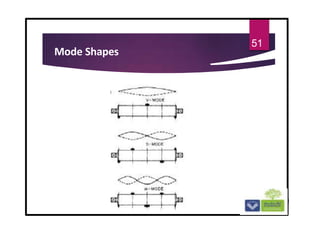
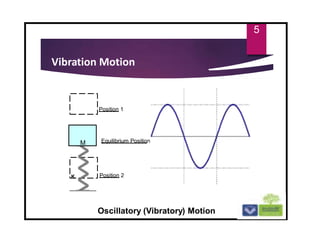
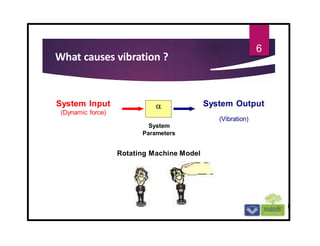
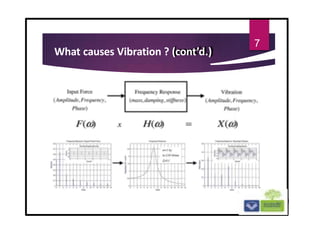
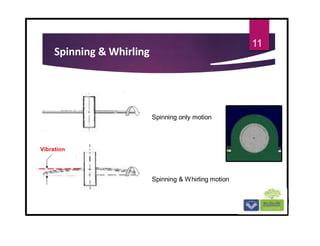
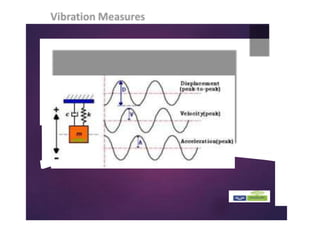
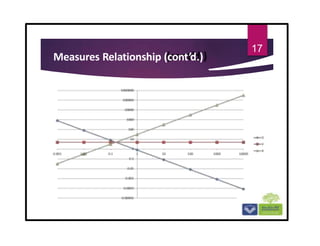
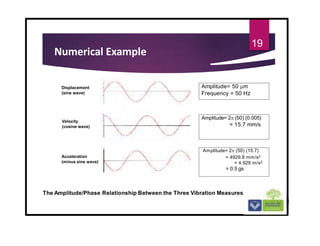
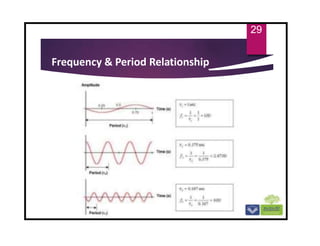
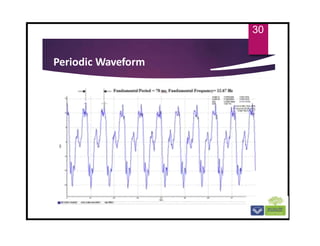
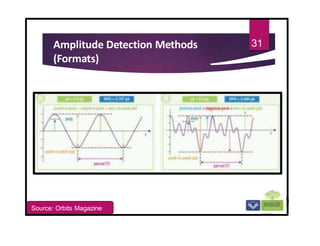
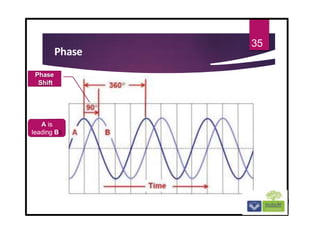
The document discusses the basics of vibrations in rotating machinery, emphasizing their importance in assessing machine condition and diagnosing faults. It outlines causes of vibrations, measurement methods, relationship between displacement, velocity, and acceleration, and key concepts like resonance and natural frequency. Additionally, it addresses factors affecting vibration behavior such as mass, stiffness, and damping.

1. “
Basics of Rotating Machinery
Vibrations
CHAPTER 1
”

2. Introduction
 The vibration of the rotating machinery contains huge
amount of information that can be utilized to determine
the machine condition, the fault producing the dynamic
forces that causes these vibrations and the severity of
these faults.
2

3. Why studying Vibration?
 Assess the condition of a machine.
 Diagnose the root causes of any excessive vibration
if any.
3

4. What is Vibration?
 Back and forth movement or oscillation of any body.
 This oscillation occurs around the body equilibrium
position.
4

5. 5
Vibration Motion
Position 1
M Equilibrium Position
K Position 2
Oscillatory (Vibratory) Motion

6. What causes vibration ?
6
System
Parameters
Rotating Machine Model

System Input
(Dynamic force)
System Output
(Vibration)

7. What causes Vibration ? (cont’d.)
7

8. Sources of Exciting Forces
 Inadequate design:
• Flexibility
• Flow pulsations
 Manufacturing defects:
• Casting cavities lead to unbalance
• Bent shaft and eccentricity
 Poor installation:
• Misalignment
• Distortion (soft foot)
• Piping strain
8

9. Sources of Exciting Forces (cont’d.)
 Abnormal operating conditions (beyond design point)
• Cavitation
• Recirculation
 Lack of proper maintenance
• Replacement of parts
• Balancing & alignment
• Lubrication
9

10. Cause & Effect Analysis
** FORCE NOT SPEED **
10
Dynamic force
(Cause)
Reaction forces
Reaction forces

11. Spinning & Whirling
11
Spinning only motion
Spinning & Whirling motion
Vibration

12. Motion Analysis
12
Motion Analysis of Unbalanced Rotor

13. Motion Analysis (cont’d.)
13

15. Vibration Measures
 Three measures; displacement,
velocity and acceleration.
 Displacement is related to the
motion.
 The velocity is related to fatigue.
 The acceleration is directly
proportional to the force.
15

16. Measures Relationship
16
Table (1.1) Vibration Measures Relationship
For harmonic (sine) wave only:
Displacement (d )= D sin(t)
Velocity (v )=
d(d)
= D cos(t)
dt
Acceleration (a)=
d(v)
=
dt dt2
d 2
(d)
= -D2
sin(t)
Where “D” is the magnitude of the displacement
signal, “” is the angular rate in rad/s and “t” is the
time.

17. Measures Relationship (cont’d.)
17

18. Typical Units
 The typical units for the displacement,
velocity and acceleration are m (microns),
mm/s and g’s respectively. The micron
equals 0.001 mm and g equals 9.81 m/s2.
18

19. Numerical Example
19
The Amplitude/Phase Relationship Between the Three Vibration Measures
Displacement
(sine wave)
Velocity
(cosine wave)
Acceleration
(minus sine wave)
Amplitude= 50 m
Frequency = 50 Hz
Amplitude= 2 (50) (0.005)
= 15.7 mm/s
Amplitude= 2 (50) (15.7)
= 4929.8 mm/s2
= 4.929 m/s2
= 0.5 gs

20. 20
D/V/A Spectra

21. Measures’ Phase Relationship
 Acceleration leads velocity by 90 degrees and leads
displacement by 180 degrees.
 In other words, displacement lags velocity by 90
degrees and lags acceleration by 180 degrees.**
We need to accelerate the body to give it
velocity to reach a distance **
21

22. Measures Conversion
 Integration and differentiation is theoretically
available.
 Practically integration only is allowed.
 Noise is a consideration.
22

23. Waves type
- Impulsive wave
- Harmonic wave
- Periodic wave
- Impact wave
- Random wave

24. 24
Harmonic vs. Periodic wave

25. Impulsive Wave
25

26. 26
Impacting

27. 27
Random

28. Signal Characteristics
 Frequency: How many
cycles per unit time.
 Reciprocal of period.
 Units: Hz, CPM & Orders
28

29. 29
Frequency & Period Relationship

30. 30
Periodic Waveform

31. Amplitude Detection Methods
(Formats)
31
Source: Orbits Magazine

32. RMS
 Analog calculation of the RMS
 Calculation from Spectrum digitally
32
n
v  v .... v
v 
2
n
RMS
2
1 2
2

33. Sources of Conflicts
 Dissimilar inputs
 Dissimilar signal processing
prior to amplitude detection
 Dissimilar amplitude
detection algorithms
 Calibration/indication
problems
33
Source: Orbits Magazine

34. Detections Conversion
34
Table (1.3) Amplitude Detections Conversion
For Harmonic (Sine) Wave Only:
RMS= 0.707 Peak
Peak= 1.414 RMS
Peak-to-Peak= 2 Peak

35. Phase
35
Phase
Shift
A is
leading B

36. Phase
36

37. In & out of phase
37
In Phase
Phase or time difference
Out of Phase

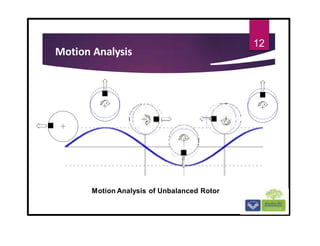
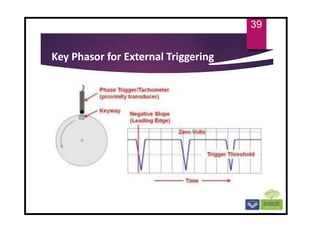
38. Phase measurements methods
 Photoelectric or laser probes. [Absolute Phase]
 Strobe light. [Obsolete]
 Dual channel analyzer. [Relative Phase]
 Key phasor. [Absolute Phase for Turbomachinery]
38

39. 39
Key Phasor for External Triggering

40. Laser of Photoelectric Probes for 40
External Triggering

41. External Triggering for Absolute
Phase Measurement
T
41

T
360o


Tacho of Key
Phasor
Pulses

42. 42
System Parameters

43. System Parameters
 Mass
 Stiffness
 Damping
43

44. Mass
 Mass is the volume of the system multiplied by the
density of its material and the typical unit of the
mass is kilograms (kg).
 The higher the mass the lower the vibration for the
same force amplitude applied.

45. Stiffness
 Stiffness is a measure of the system elasticity and is
defined as the deflection caused by applying unit
force to the system.
 Stiffness is typically expressed in Newton per meter
(N/m).
 The higher the stiffness, the lower the vibration
amplitudes resulted from same force applied.

46. Damping
 Damping is defined as the ability of the system to
dissipate energy into heat (i.e. converts the kinetic
energy of motion or vibration into heat energy).
 The damping is expressed in Newton per millimeter
per second (N/mm/s).
 The highest the damping in the system, the lower
the vibration amplitude for the same force.

47. Natural Frequency
Where:
 n: natural frequency (rad/s)
 k: stiffness (N/m)
 m: mass (kg)

48. Resonance
 Resonance is a condition at which the frequency of
one of the exciting forces is close or equal to one of
the natural frequencies of the system.
 In this case, the system will vibrate severely since the
system will work as an amplifier that converts all
energy into vibratory motion.
 The term "resonance" is typically used with
structures; when discussing the natural frequencies
of a rotor, the term "Critical “peed" is typically used.

49. Resonance
Related to structures.
Depends on mass and stiffness.
System acts as amplifier.
49
100 Hz by 50 Hz 100 Hz by 100 Hz 100 Hz by 200 Hz
Video: Ground Test
Video: Bridge

50. Critical Speeds
 The critical speeds are the speeds at which an
exciting force frequency is very close or equals to
one of the rotor natural frequencies.
 In other words, the critical speed is the speed at
which the resonance occurs in the rotor. For each
critical speed, there is a unique deflection shape of
the rotor known as "Mode “hape".

51. Mode Shapes
51

52. 3D Mode Shapes
52
Link to Video

53. 53
Questions??