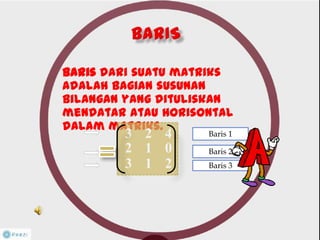
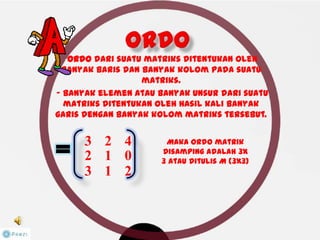
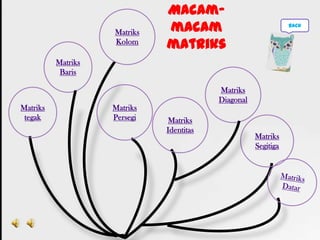
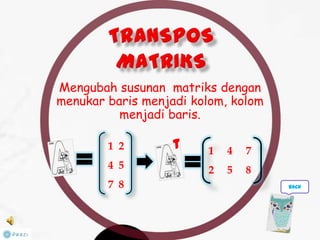
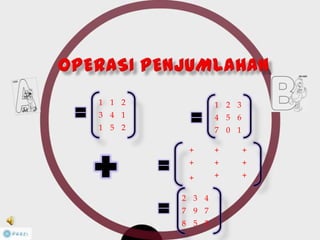
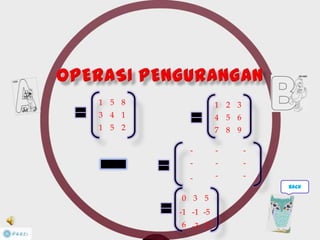
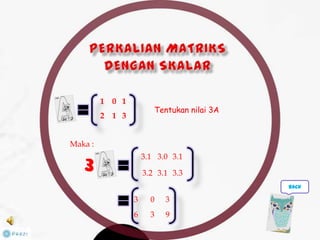
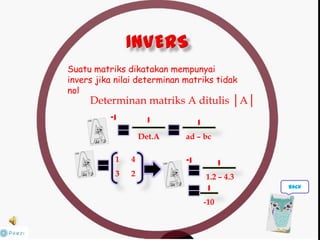
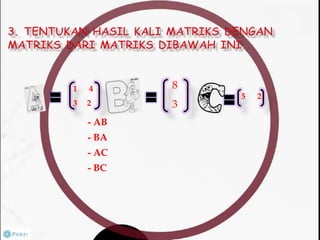
Dokumen ini membahas tentang konsep matriks dalam pendidikan matematika, termasuk definisi, jenis-jenis, dan operasi aljabar dasar pada matriks. Terdapat penjelasan mengenai ordo matriks, elemen, dan sifat-sifat seperti komutatif dan asosiatif dalam penjumlahan. Selain itu, dibahas juga tentang kondisi untuk matriks dapat dikalikan dan konsep invers yang berhubungan dengan determinan.

1. Pendidikan Matematika
Universitas Sanata
Dharma 2013

2. Mate
ri

4. Standar Kompetensi (SK):
Menggunakan konsep matriks dalam
pemecahan masalah.
Kompetensi Dasar (KD):
Menggunakan sifat-sifat dan operasi
matriks.
back

5. 1. mengenal definisi matriks
dan jenis-jenis matriks
2. Melakukan operasi
aljabar pada matriks
back

7. Matriks adalah kelompok bilangan
yang disusun dalam suatu jajaran
berbentuk persegi atau persegi
panjang yang terdiri atas baris-
baris dan kolom-kolom.

8. Jadi dari kumpulan bilangan
dibawah ini yang merupakan
matriks adalah......3
6 8
5
Atau yang ini?
89
5
Yang ini kah?
back

9. Nama matriks dari sebuah
matriks adalah sebuah huruf
kapital yang digunakan untuk
menamai sebuah matriks.
3 2 4
2 1 0
3 1 2
back

10. BEBERAPA ISTILAH DALAM
MATRIKS
back

11. Baris dari suatu matriks
adalah bagian susunan
bilangan yang dituliskan
mendatar atau horisontal
dalam matriks.
3 2 4
2 1 0
3 1 2
Baris 1
Baris 2
Baris 3

12. Kolom dari suatu matriks
adalah bagian yang dituliskan
tegak atau vertikal dalam
matriks.
3 2 4
2 1 0
3 1 2
kolom1
kolom2
kolom3

13. Elemen atau unsur suatu matriks
adalah bilangan-bilangan (real
atau kompleks) yang menyusun
matriks itu
3 2 4
2 1 0
3 1 2
Elemen pada baris
pertama kolom pertama
Elemen pada baris
tiga kolom kedua
Ada yang tau angka ini ada
pada kolom berapa dan
pada baris berapa?

14. -Ordo dari suatu matriks ditentukan oleh
banyak baris dan banyak kolom pada suatu
matriks.
-- banyak elemen atau banyak unsur dari suatu
matriks ditentukan oleh hasil kali banyak
garis dengan banyak kolom matriks tersebut.
Maka ordo matrik
disamping adalah 3x
3 atau ditulis M (3x3)
3 2 4
2 1 0
3 1 2

15. 1 2 3
4 5 6
7 8 9
Nama matriks?
Ada berapa baris matrik
tersebut?
Ada berapa kolom matriks
tersebut?
Jadi, ordo matriks tersebut?
Sebutkan elemen-elemen
matriks tersebut!

16. Matriks
Segitiga
Matriks
Baris
Matriks
Kolom
Matriks
Persegi Matriks
Identitas
Matriks
Diagonal
Macam-
macam
matriks
Matriks
tegak
back

17. Jika sebuah Matriks berordo m × n, dengan
nilai m=1 sehingga diperoleh matriks
berordo 1 x n. Matriks 1 x n terdiri atas
satu baris dan memuat n elemen
Contoh
1 2 3
back

18. Jika sebuah Matriks berordo m × n, dengan
nilai n =1 sehingga diperoleh matriks
berordo 1 x m. Matriks 1 x m terdiri atas
satu baris dan memuat m elemen
4
5
6
Contoh
back

19. Jika sebuah Matriks berordo m × n, dengan
nilai m = n sehingga diperoleh matriks
berordo n x n (bisa disebut matrik n). Pada
Matriks berordo n, banyak baris = banyak
kolom.
5 6
7 8
Contoh
Matriks berordo 2 x 2 atau M2

20. Pada sebuah matriks persegi, elemen
yang terletak pada garis hubung
elemen a11 dengan elemen amn
dinamakan sebagai diagonal utama
(DU). Sedangkan elemen yang terletak
pada garis hubung elemen an1 dengan
elemen an1 dinamakan sebagai
diagonal samping (DS).
1 2 3
4 5 6
7 8 9
Diagonal Utama
(DU)
Diagonal Samping
(DS)
A =
Contoh
back

21. MATRIKS SEGITIGA
ATAS
MATRIKS SEGITIGA
BAWAH
Matriks segitiga atas
dengan elemen dibawah
diagonal utama semuanya
bernilai nol.
Matriks segitiga bawah
dengan elemen diatas
diagonal utama semuanya
bernilai nol.
𝐴 =
4 3
0 1
2 −1
3 5
0 0
0 0
2 6
0 4
𝐴 =
4 0
6 1
0 0
0 0
2 −1
3 5
2 0
3 4
back

22. Jika sebuah Matriks berordo n, dengan elemen
matriks yang berada dibawah dan diatas
diagonal utama semuanya bernilai nol. Maka
artinya semua elemen matrik bernilai nol,
kecuali elemen yang terletak pada diagonal
utama.
5 0
0 8
1 0 0
0 5 0
0 0 9
back

23. Jika sebuah Matriks berordo n,
dengan elemen pada diagonal utama
semuanya bernilai 1. lambang nya In
1 0 0
0 1 0
0 0 1
1 0
0 1I2
I3
back

24. Jika sebuah Matriks berordo m x n, dengan
m < n , berarti banyak kolom lebih banyak
dibandingkan banyak barisnya. Oleh karena
itu bentuknnya akan memanjang.
1 5 8 5
0 1 0 3
back

25. Jika sebuah Matriks berordo m x n,
dengan m > n , berarti banyak baris lebih
banyak dibandingkan banyak
kolomnyanya. Oleh karena itu
bentuknnya akanpersegi panjang tegak.
1 5
2 8
0 1
back

26. Mengubah susunan matriks dengan
menukar baris menjadi kolom, kolom
menjadi baris.
1 2
4 5
7 8
t 1 4 7
2 5 8
back

27. back

28. 1. - Ordo kedua matriks yang
dijumlahkan/ dikurangkan harus sama
2. - Setiap unsur yang letaknya
bersesuaian dijumlahkan /dikurangkan.

29. 1 1 2
3 4 1
1 5 2
1 2 3
4 5 6
7 0 1
+ + +
+ + +
+ + +
2 3 4
7 9 7
8 5 3

30. 1. Sifat Komutatif : A + B = B+A
1. 2. Sifat Asosiatif : (A+B)+C=A+(B+C)
2. 3. Terdapat matriks identitas O yang bersifat :
A+O=O+A=A
3. 4. Semua matriks A mempunyai lawan atau
back

31. 1 5 8
3 4 1
1 5 2
1 2 3
4 5 6
7 8 9
- - -
- - -
- - -
0 3 5
-1 -1 -5
6 -3 -7
back

32. 1 0 1
2 1 3
Tentukan nilai 3A.
Maka :
3
3.1 3.0 3.1
3.2 3.1 3.3
3 0 3
6 3 9
back

33. Syarat 2 matriks bisa dikalikan jika banyak
kolom matriks pertama harus sama dengan
banyaknya baris matriks kedua
1 2 0
2 1 3
1
0
2
1
8
1
0
2

34. back

35. Suatu matriks dikatakan mempunyai
invers jika nilai determinan matriks tidak
nol
Determinan matriks A ditulis │A│
-1 1
Det.A
1
ad – bc
1 4
3 2
-1 1
1.2 – 4.3
1
-10
back

36. Barisan bilangan yang di tulis di
antara dua garis tegak
Det.A = = 1.2 – 4.3 = – 10
RUMUS : Det.A =
a b
c d
= ad – bc
1 4
3 2
back

38. 1
2
3

39. a. A + B – C
b. A – B – C
c. A + B + C
1 -2
4 2
1 -2
4 2
0 5
3 -2

40. 4 9
2 10

41. - AB
- BA
- AC
- BC
1 4
3 2
8
3
5 2