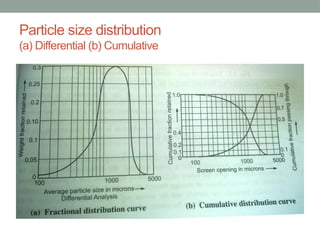
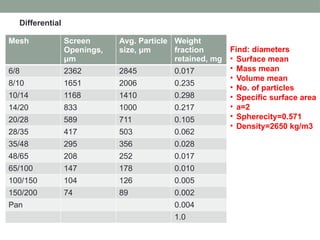
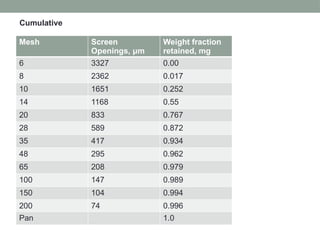
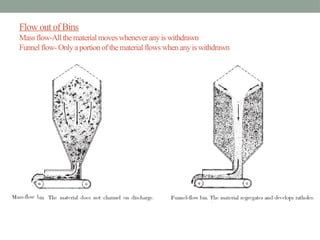
The document outlines mechanical operations in chemical engineering, focusing on particle size analysis, including concepts of shape, size, distribution, and methods such as screening and sedimentation. It discusses the calculation of particle sphericity, mean diameters, and the importance of screening in ensuring the correct sizing of materials for processing. Additionally, it addresses storage methods for solids, with examples involving pressure estimation in silos filled with different materials.

1. MECHANICAL OPERATIONS
(CHE1022)
Dr. Aabid Hussain Shaik
Associate Professor
Chemical Engineering Department,
SCHEME
Contact information:
Room no. SMV 221
Email: aabidhussain.s@vit.ac.in

2. Module 1
• Introduction to particulate solids
• Particle shape, size
• Mixed particle sizes
• Size analysis – cumulative and differential
• Various mean diameters
• Screen analysis
• Standard screens
• Various Industrial screens
• LO’s
• Will be able to use different size analysis methods to determine
particle size.
• Will be able to calculate the particle size distribution using screen
analysis.

3. Particulate – Assembly of small particles
They are characterized by
*Size
*Shape
*Density
Regular –specified by size, shape
Irregular-arbitrarily defined

4. •
Equivalent diameter (irregular shaped particles)

5. •
Volume: V
Sp
• Sphericity (Φs)
𝜙𝑠=
6𝑉 𝑝
𝐷𝑝 𝑆𝑝
where Vp is the volume of the particle, Ap is its
surface area, and Dp is the diameter of a sphere
with the same volume
Answer: 0.806

6. Spherecity of cube
• Ψ = As / Ap Where: As is the surface area of the equivalent
sphere and Ap is the measured surface area.
The sphericity can have a value ranging from 0-1, where Ψ = 1
for an ideal sphere.
• The volume of a spherical particle is:
• Vp= (1/6) π dp
3
Where: dp is the diameter of the particle.
• The surface area of a sphere is:
• As = π dp
2
= π [ (6 Vp / π)(1/3)
]2
Thus, for a particle, Ψ can be
calculated by measuring its volume and surface area:
• Ψ = As / Ap = π (6 Vp / π)(2/3)
/ Ap An example: A cube measuring
1 × 1 × 1 cm has a volume of 1 cm3
, and a surface area of 6 ×
(1 × 1) = 6 cm2
. Its sphericity is:
• Ψ = π × (6 × 1 / π)(2/3)
/ 6 = 0.806

7. Calculate the sphericity of a cylinder of dia 1 cm and height 3 cm.
• Spherecity = surface area of the sphere of same volume
as the particle/surface area of the particle
• Volume of particle = ∏rc
2
h = p x 0.52
x 3 = 2.356 cm3
• Radius of sphere of volume 2.356 cm3
:
• 4 ∏ rs
3
/ 3 = 2.356
• rs = 0.8255 cm
• Surface area of sphere of same volume as the particle =
4 ∏ rs
2
= 4 x p x 0.82552
= 8.563 cm2
• Surface area of particle = 2 ∏ rc (h + rc) = 2 x p x 0.5 x (3
+ 0.5) = 10.996 cm2
• Sphericity (f s) = 8.563/10.996 = 0.779

8. Calculate shperecity of a cylinder having diameter 1
cm and height 5 cm

9. Particle size- specified by diameter.
Size expressed in different units according to size range
*coarse – inch (or) mm
*Fine - screen size (mesh)
*Very fine - µm (or) nm
*Ultra fine – m2
/gm (specific surface area)

10. Mixture of particles (same size)
No. of particles in the sample
Total surface area

11. Specific surface of mixture(different size)
+…+
xi is the mass fraction

12. Number of particles in Mixture (Different sizes)
𝑁𝑤 =
1
𝑎𝜌𝑝
∑
𝑖=1
𝑛
𝑥𝑖
𝐷𝑝𝑖❑
3
=
1
𝑎𝜌𝑝 𝐷𝑣❑
3
𝑣𝑝=𝑎 𝐷𝑝
3
Volume shape factor:
Volume is proportional of cube of diameter, the constant of proportionality is
knows as volume shape factor (a).
a=π/6 for spheres

13. Average particle size
Volume – Surface mean diameter

14. Arithmetic mean diameter
𝐷 𝑁 =
∑
𝑖=1
𝑛
( 𝑁 𝑖 𝐷𝑝𝑖 )
∑
𝑖=1
𝑛
𝑁𝑖
=
∑
𝑖 =1
𝑛
( 𝑁 𝑖 𝐷𝑝𝑖 )
𝑁 𝑇

15. Mass mean diameter
𝐷𝑤 =∑
𝑖=1
𝑛
(𝑥𝑖 𝐷𝑝𝑖)

16. Volume mean diameter

17. Determining Particle Size:
Various methods are used for measurement of particle size.
These depends on size range, the physical properties and the
condition of dryness or wetness.
The following methods are used in laboratory.
1. Microscope
2. Screening
3. Sedimentation
4. Elutriation
5. Centrifuging

18. Screening (Sieving)
Importance of screening:
• Removes the fine from the feed material before a reduction equipment.
• Prevents oversized material to enter into unit operations.
• Produce a process grade material to meet specific feed size.
• Removes fines from finished product before packing.

19. Types of standard screens:
1. Tyler standard screen series
2. Indian standard test sieves
Types of Screen/sieve analysis
3. Differential Analysis
4. Cumulative Analysis
The mesh number system is a measure
of how many openings there are per
linear inch in a screen. Sizes vary by a
factor of √2. This can easily be
determined as screens are made from
wires of standard diameters, however,
opening sizes can vary slightly due to
wear and distortion.

20. Particle size distribution
(a) Differential (b) Cumulative

21. Mesh Screen
Openings,
μm
Avg. Particle
size, μm
Weight
fraction
retained, mg
6/8 2362 2845 0.017
8/10 1651 2006 0.235
10/14 1168 1410 0.298
14/20 833 1000 0.217
20/28 589 711 0.105
28/35 417 503 0.062
35/48 295 356 0.028
48/65 208 252 0.017
65/100 147 178 0.010
100/150 104 126 0.005
150/200 74 89 0.002
Pan 0.004
1.0
Differential
Find: diameters
• Surface mean
• Mass mean
• Volume mean
• No. of particles
• Specific surface area
• a=2
• Spherecity=0.571
• Density=2650 kg/m3

22. • Surface mean diameter
• Mass mean diameter
• Volume mean diameter
• Number of particles
• Specific surface area
𝐷𝑤 =∑
𝑖=1
𝑛
(𝑥𝑖 𝐷𝑝𝑖)
𝑁𝑤 =
1
𝑎𝜌𝑝
∑
𝑖=1
𝑛
𝑥𝑖
𝐷𝑝𝑖❑
3
=
1
𝑎𝜌𝑝 𝐷𝑣❑
3
+…+

23. Mesh Screen
Openings, μm
Weight fraction
retained, mg
6 3327 0.00
8 2362 0.017
10 1651 0.252
14 1168 0.55
20 833 0.767
28 589 0.872
35 417 0.934
48 295 0.962
65 208 0.979
100 147 0.989
150 104 0.994
200 74 0.996
Pan 1.0
Cumulative

24. Storage of solids
1. Bulk storage
2. Bin storage
Bin - not so tall but usually wider
Silo – tall and relatively small in diameter
Hopper - vessel with sloping at the bottom

25. Flow out of Bins
Massflow-All thematerialmoveswheneverany iswithdrawn
Funnel flow- Onlyaportionofthematerial flowswhenanyiswithdrawn

26. Best flow depends on the following physical characteristics of
materials.
1. Particle size
2. Moisture content
3. Temperature
4. Age
5. Oil content.

27. Problems
• A large welded steel silo 4 m in diameter and 20 m high is
to be built. The silo has a central discharge on a flat
bottom. Estimate the pressure on the wall, at the bottom
of of the silo if the silo is filled with (a) coal particles and
(b) water. The coal particles have the following
characteristics:
• Density = 560 kg/m3
• Ø = 20 degrees
• Jannesen coefficient = 0.4

28. Problem
• A large welded steel silo 12 ft in diamter and 60 ft high is
to be built. The silo has a central discharge on a flat
bottom. Estimate the pressure on the wall at the bottom of
the silo filled with (a) plastic pellets and (b) water. The
plastic pellet have the following characteristics:
Density = 35 lb/cu ft
Ø = 20 degrees
Jannesen coefficient = 0.4