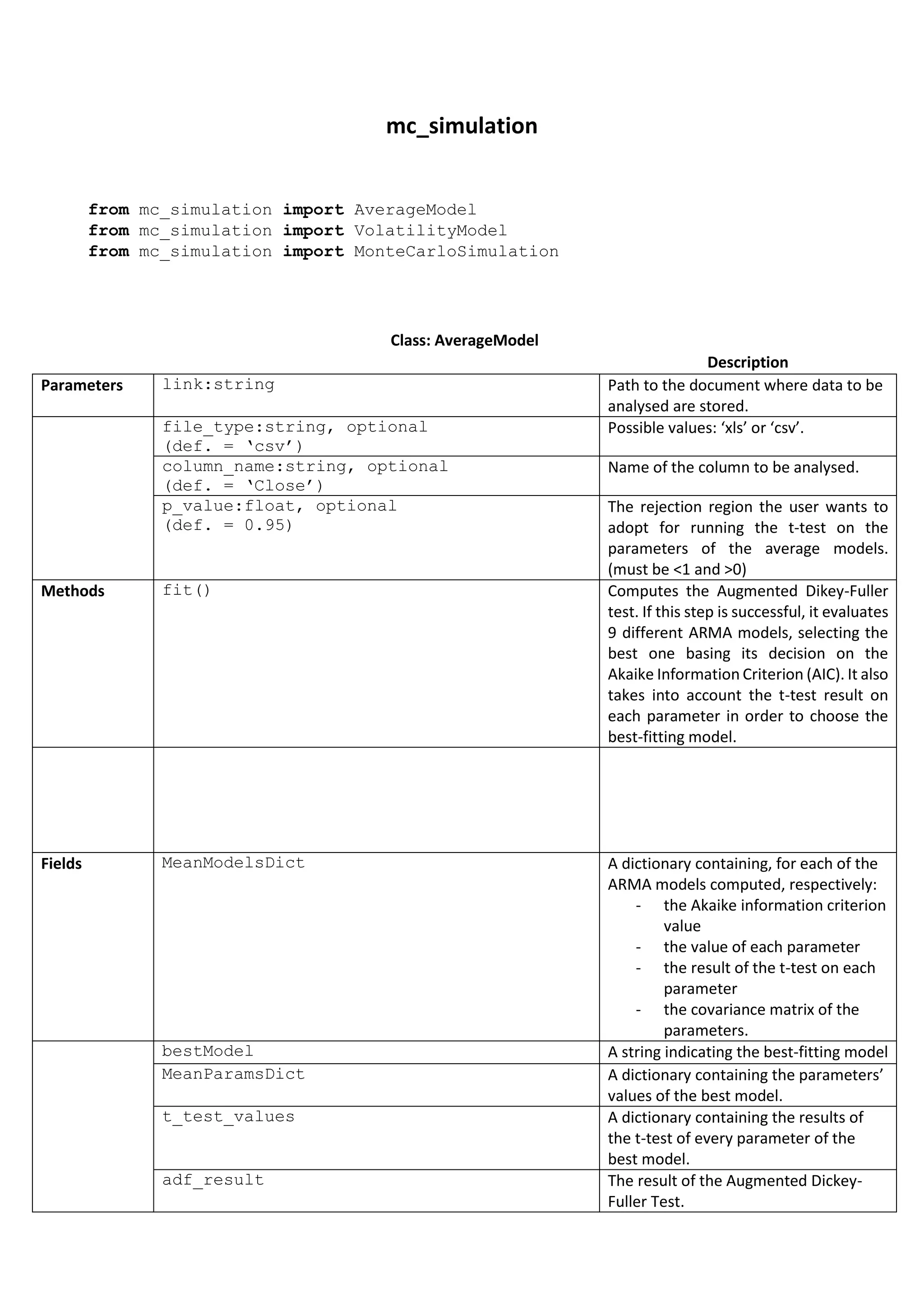
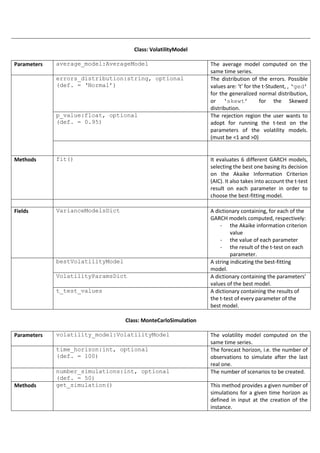
The document describes three Python classes - AverageModel, VolatilityModel, and MonteCarloSimulation - for modeling time series data and performing Monte Carlo simulations. AverageModel fits autoregressive moving average (ARMA) models to time series data to model the average and selects the best model. VolatilityModel fits generalized autoregressive conditional heteroskedasticity (GARCH) models to model volatility and selects the best model. MonteCarloSimulation uses the selected average and volatility models to generate multiple scenarios through Monte Carlo simulation over a specified time horizon and number of simulations. It provides methods to return simulated scenarios and statistics.

1. mc_simulation
from mc_simulation import AverageModel
from mc_simulation import VolatilityModel
from mc_simulation import MonteCarloSimulation
Class: AverageModel
Description
Parameters link:string Path to the document where data to be
analysed are stored.
file_type:string, optional
(def. = ‘csv’)
Possible values: ‘xls’ or ‘csv’.
column_name:string, optional
(def. = ‘Close’)
Name of the column to be analysed.
p_value:float, optional
(def. = 0.95)
The rejection region the user wants to
adopt for running the t-test on the
parameters of the average models.
(must be <1 and >0)
Methods fit() Computes the Augmented Dikey-Fuller
test. If this step is successful, it evaluates
9 different ARMA models, selecting the
best one basing its decision on the
Akaike Information Criterion (AIC). It also
takes into account the t-test result on
each parameter in order to choose the
best-fitting model.
Fields MeanModelsDict A dictionary containing, for each of the
ARMA models computed, respectively:
- the Akaike information criterion
value
- the value of each parameter
- the result of the t-test on each
parameter
- the covariance matrix of the
parameters.
bestModel A string indicating the best-fitting model
MeanParamsDict A dictionary containing the parameters’
values of the best model.
t_test_values A dictionary containing the results of
the t-test of every parameter of the
best model.
adf_result The result of the Augmented Dickey-
Fuller Test.

2. Class: VolatilityModel
Parameters average_model:AverageModel The average model computed on the
same time series.
errors_distribution:string, optional
(def. = ‘Normal’)
The distribution of the errors. Possible
values are: ‘t’ for the t-Student, , ‘ged’
for the generalized normal distribution,
or ‘skewt’ for the Skewed
distribution.
p_value:float, optional
(def. = 0.95)
The rejection region the user wants to
adopt for running the t-test on the
parameters of the volatility models.
(must be <1 and >0)
Methods fit() It evaluates 6 different GARCH models,
selecting the best one basing its decision
on the Akaike Information Criterion
(AIC). It also takes into account the t-test
result on each parameter in order to
choose the best-fitting model.
Fields VarianceModelsDict A dictionary containing, for each of the
GARCH models computed, respectively:
- the Akaike information criterion
value
- the value of each parameter
- the result of the t-test on each
parameter.
bestVolatilityModel A string indicating the best-fitting
model.
VolatilityParamsDict A dictionary containing the parameters’
values of the best model.
t_test_values A dictionary containing the results of
the t-test of every parameter of the
best model.
Class: MonteCarloSimulation
Parameters volatility_model:VolatilityModel The volatility model computed on the
same time series.
time_horizon:int, optional
(def. = 100)
The forecast horizon, i.e. the number of
observations to simulate after the last
real one.
number_simulations:int, optional
(def. = 50)
The number of scenarios to be created.
Methods get_simulation() This method provides a given number of
simulations for a given time horizon as
defined in input at the creation of the
instance.

3. get_extreme_scenarios()
parameters:
- criterion: string. Possible values:
‘returns_average’ (def.), ‘last_obs’
This method returns the best and worst
scenarios of the simulation created with
the previous method. The best and
worst are so defined accordingly to two
possible criteria:
- the average of the returns
- the last observation
get_conf_interval()
parameters:
- conf_interval: float. Admitted values’
interval: [1.0 ; 0.5[
- criterion: string. Possible values:
‘returns_average’ (def.), ‘last_obs’
This method returns the scenario at the
x percentile (where x must be specified),
and at the 1-x percentile. The value must
be between 1 and 0.5. The best and
worst are so defined accordingly to two
possible criteria:
- the average of the returns
- the last observation.
get_average() This method shows the average of all
scenarios previously generated,
providing also the last observation’s
value.