This document discusses quadratic forms and their properties. It provides examples of reducing a quadratic form to canonical form to determine its nature, rank, index, and signature. The key steps are: 1) Find the characteristic equation and eigenvalues of the coefficient matrix 2) Determine the eigenvectors to obtain the modal matrix 3) Normalize the eigenvectors to obtain the normalized matrix for diagonalization

1. Matrices
Quadratic forms

2. Quadratic forms
Calculus and Linear Algebra 2

3. Nature of the Quadratic form using sub determinant method
Let 𝑨 be any square matrix and
Calculus and Linear Algebra 3

4. Calculus and Linear Algebra 4
It is indefinite for all other cases.
,…

5. Calculus and Linear Algebra 5

6. Problem
Calculus and Linear Algebra 6
Solution:

7. Calculus and Linear Algebra 7
Solution:
Solution:
1

8. Calculus and Linear Algebra 8
Solution:

9. Calculus and Linear Algebra 9
Solution:

10. Calculus and Linear Algebra 10
Solution:

11. Rank of a quadratic form
The rank of the coefficient matrix A is called the rank of the
quadratic form 𝑥𝑇𝐴𝑥. The number of nonzero eigenvalues of A also
gives the rank of the quadratic form of A
Index
The number of positive terms in the canonical form is called
the index of the quadratic form and is denoted by p.
Calculus and Linear Algebra 11

12. Signature
The difference between the number of positive and negative terms in the
canonical form is called the signature of the quadratic form and is denoted by s.
Calculus and Linear Algebra 12

13. Reduce the quadratic form 6x1
2
+ 3x2
2
+ 3x3
2
− 4x1x2 + 4x1x3 −
2x2x3 to a canonical form using orthogonal transformation. Also
find its nature, rank, index and signature.
Solution:
Given QF: 6x1
2
+ 3x2
2
+ 3x3
2
− 4x1x2 + 4x1x3 − 2x2x3
The matrix form of the QF is 𝑋𝑇𝐴𝑋, where 𝑋 =
𝑥1
𝑥2
𝑥3
13

14. 𝐴 =
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥1
2
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥1𝑥2
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥1𝑥3
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥1𝑥2 𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥2
2
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥2𝑥3
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥1𝑥3
1
2
𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥2𝑥3 𝑐𝑜𝑒𝑓𝑓 𝑜𝑓 𝑥3
2
𝐴 =
6 −2 2
−2 3 −1
2 −1 3
14

15. i) To find the characteristic equation of A
The characteristic equation is 𝜆3 − 𝑠1𝜆2 + 𝑠2𝜆 − 𝑠3 = 0
𝑠1 = the sum of diagonal elements = 6 + 3 + 3 = 12
𝑠2 = sum of the minors of the principle diagonal
=
3 −1
−1 3
+
6 2
2 3
+
6 −2
−2 3
= 8 + 18 − 4 + 18 − 4
= 8 + 14 + 14 = 36
15

16. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 -12 36 -32
0
16

17. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0
17

18. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0
1
18

19. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1
1
19

20. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1
1 -11
20

21. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1 -11
1 -11
21

22. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1 -11
1 -11 25
22

23. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1 -11 25
1 -11 25
23

24. 𝑠3 = det 𝐴 =
6 −2 2
−2 3 −1
2 −1 3
= 6 8 + 2 −4 + 2(−4) = 32
∴ The characteristic equation is 𝜆3
− 12𝜆2
+ 36𝜆 − 32 = 0
To solve this cubic equation we use synthetic division method
1 1 -12 36 -32
0 1 -11 25
1 -11 25 -7 ≠ 0
24

25. So we try with next possible number 2
2 1 -12 36 -32
0 2 -20 32
1 -10 16 0
So one of the root is 2 and we have 𝜆2
− 10𝜆 + 16 = 0
25

26. 𝜆2 − 10𝜆 + 16 = 0
𝜆 − 8 𝜆 − 2 = 0
𝜆 = 8, 2
The eigenvalues are 8, 2, 2.
26

27. ii) To find eigenvectors:
We have 𝐴 − 𝜆𝐼 𝑋 = 0
6 −2 2
−2 3 −1
2 −1 3
−
𝜆 0 0
0 𝜆 0
0 0 𝜆
𝑥1
𝑥2
𝑥3
= 0
6 − 𝜆 −2 2
−2 3 − 𝜆 −1
2 −1 3 − 𝜆
𝑥1
𝑥2
𝑥3
= 0
27

28. Case (i) when 𝜆 = 8
6 − 8 −2 2
−2 3 − 8 −1
2 −1 3 − 8
𝑥1
𝑥2
𝑥3
= 0
−2 −2 2
−2 −5 −1
2 −1 −5
𝑥1
𝑥2
𝑥3
= 0
Now we write the above matrix as a system of equations
28

29. −2𝑥1 − 2𝑥2 + 2𝑥3 = 0 ⇒ −𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
2𝑥1 − 𝑥2 − 5𝑥3 = 0
By cross multiply method, we solve these equation
Consider any two equations, now let’s take first two
−𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
𝑥1
−1 1
29

30. −2𝑥1 − 2𝑥2 + 2𝑥3 = 0 ⇒ −𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
2𝑥1 − 𝑥2 − 5𝑥3 = 0
By cross multiply method, we solve these equation
Consider any two equations, now let’s take first two
−𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
𝑥1
−1 1
−2 −5
30

31. −2𝑥1 − 2𝑥2 + 2𝑥3 = 0 ⇒ −𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
2𝑥1 − 𝑥2 − 5𝑥3 = 0
By cross multiply method, we solve these equation
Consider any two equations, now let’s take first two
−𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
𝑥1
−1 1
−2 −5
=
−𝑥2
−1 1
−2 −1
31

32. −2𝑥1 − 2𝑥2 + 2𝑥3 = 0 ⇒ −𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
2𝑥1 − 𝑥2 − 5𝑥3 = 0
By cross multiply method, we solve these equation
Consider any two equations, now let’s take first two
−𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 − 5𝑥2 − 𝑥3 = 0
𝑥1
−1 1
−5 −1
=
−𝑥2
−1 1
−2 −1
=
𝑥3
−1 −1
−2 −5
32

33. 𝑥1
−1 1
−5 −1
=
−𝑥2
−1 1
−2 −1
=
𝑥3
−1 −1
−2 −5
𝑥1
6
=
−𝑥2
3
=
𝑥3
3
𝑿𝟏 =
𝟔
−𝟑
𝟑
=
𝟐
−𝟏
𝟏
33

34. Case (ii) when 𝜆 = 2
6 − 2 −2 2
−2 3 − 2 −1
2 −1 3 − 2
𝑥1
𝑥2
𝑥3
= 0
4 −2 2
−2 1 −1
2 −1 1
𝑥1
𝑥2
𝑥3
= 0
Now we write the above matrix as a system of equations
34

35. 4𝑥1 − 2𝑥2 + 2𝑥3 = 0 ⇒ 2𝑥1 − 𝑥2 + 𝑥3 = 0
−2𝑥1 + 𝑥2 − 𝑥3 = 0
2𝑥1 − 𝑥2 + 𝑥3 = 0
All the equations are same.
Consider one equation, now let’s consider 𝑥1 = 0
2(0) − 𝑥2 + 𝑥3 = 0 ⇒ 𝑥2 = 𝑥3
𝑿𝟐 =
𝟎
𝟏
𝟏
35

36. Case (iii) when 𝜆 = 2 is a repeated root
From orthogonal transformation we know that,
𝑋1𝑋2
𝑇
= 0; 𝑋2𝑋3
𝑇
= 0 and 𝑋3𝑋1
𝑇
= 0
Let 𝑋3 =
𝑎
𝑏
𝑐
,
𝑋2𝑋3
𝑇
=
0
1
1
𝑎 𝑏 𝑐 ⇒ 0𝑎 + 𝑏 + 𝑐 = 0
𝑋1𝑋3
𝑇
=
2
−1
1
𝑎 𝑏 𝑐 ⇒ 2𝑎 − 𝑏 + 𝑐 = 0
36

37. 2𝑎 − 𝑏 + 𝑐 = 0
0𝑎 + 𝑏 + 𝑐 = 0
By cross multiply method, we solve these equation
𝑎
−1 1
1 1
=
−𝑏
2 1
0 1
=
𝑐
2 −1
0 1
𝑎
−2
=
−𝑏
2
=
𝑐
2
37

38. 𝑿𝟑 =
−𝟏
−𝟏
𝟏
Modal matrix 𝑀 =
2 0 −1
−1 1 −1
1 1 1
Normalization 𝑋1 = 22 + −1 2 + 12 = 6
𝑋2 = 02 + 1 2 + 12 = 2
𝑋3 = (−1)2+ −1 2 + 12 = 3
38

39. Normalised matrix 𝑁 =
2/ 6 0 −1/ 3
−1/ 6 1/ 2 −1/ 3
1/ 6 1/ 2 1/ 3
Diagonalization 𝐷 = 𝑁𝑇𝐴𝑁
𝐷 =
2/ 6 −1/ 6 1/ 6
0 1/ 2 1/ 2
−1/ 3 −1/ 3 1/ 3
6 −2 2
−2 3 −1
2 −1 3
2/ 6 0 −1/ 3
−1/ 6 1/ 2 −1/ 3
1/ 6 1/ 2 1/ 3
𝐷 =
8 0 0
0 2 0
0 0 2
39

40. Let 𝑋 = 𝑁𝑌 be an orthogonal transformation which changes the
quadratic form to canonical form where 𝑌 =
𝑦1
𝑦2
𝑦3
We know 𝑄𝐹 = 𝑋𝑇𝐴𝑋 ⟹ 𝑄 = 𝑁𝑌 𝑇𝐴(𝑁𝑌)
𝑄 = 𝑌𝑇𝑁𝑇𝐴𝑁𝑌
𝑄 = 𝑌𝑇(𝑁𝑇𝐴𝑁)𝑌
𝑄 = 𝑌𝑇𝐷𝑌
⟹ (𝑦1 𝑦2 𝑦3)
8 0 0
0 2 0
0 0 2
𝑦1
𝑦2
𝑦3
40

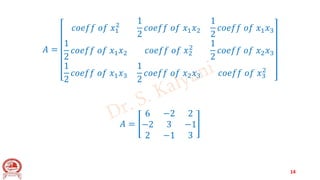
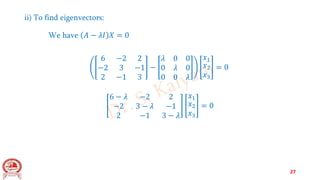
41. 8𝑦1
2
+ 2𝑦2
2
+ 2𝑦3
2
which is the canonical form of the canonical form.
• Nature of Quadratic Form is positively definite [Since all the Eigen
values are positive]
• Rank of the Quadratic Form is 3 [No. of non-zero Eigen values ]
• Index of the Quadratic Form is 3 [No. of positive Eigen values ]
• Signature of the Quadratic Form is 3. [No. of positive Eigen
values−No. of negative Eigen values ]
41

42. Home connection
Calculus and Linear Algebra 42