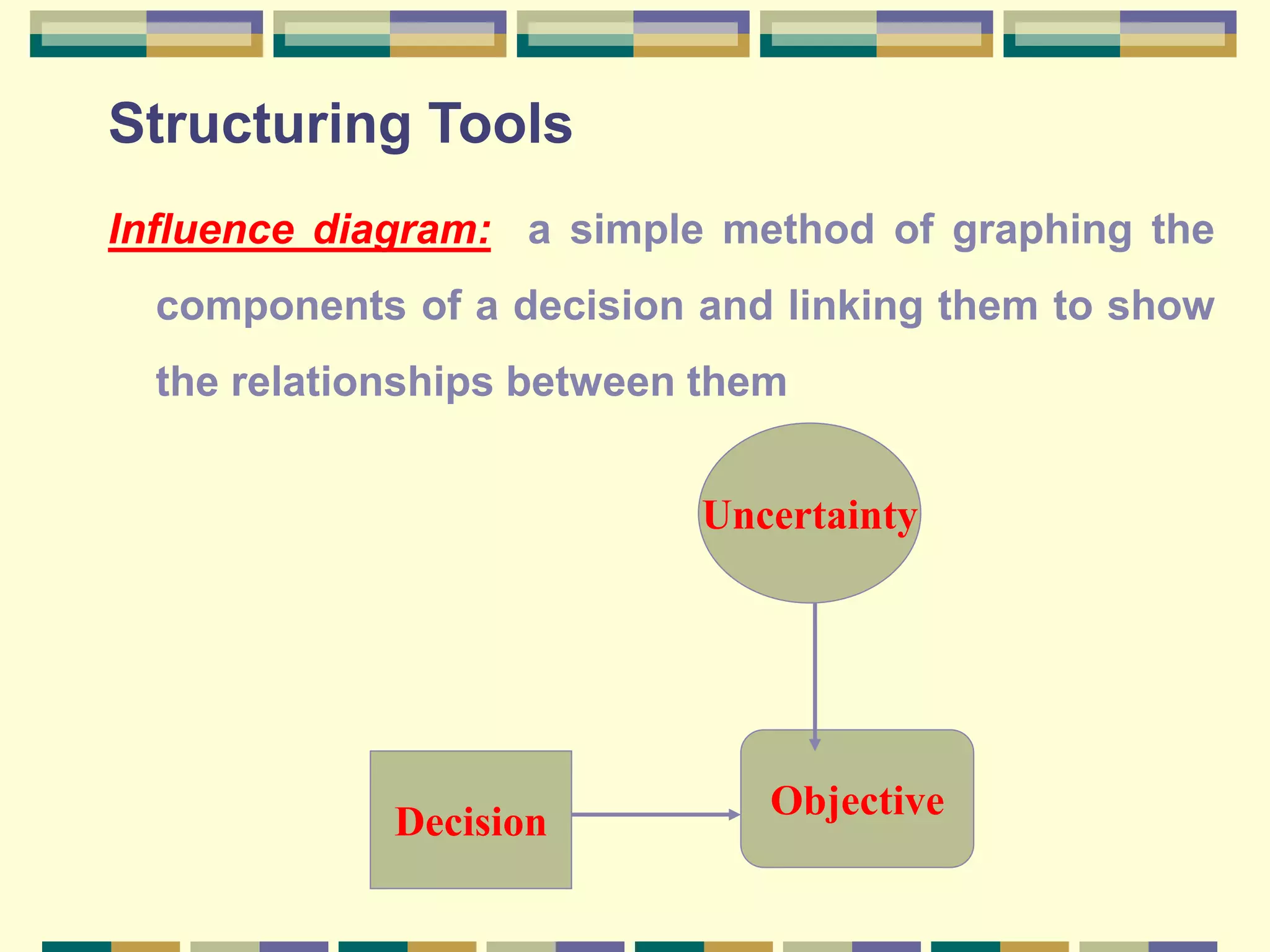
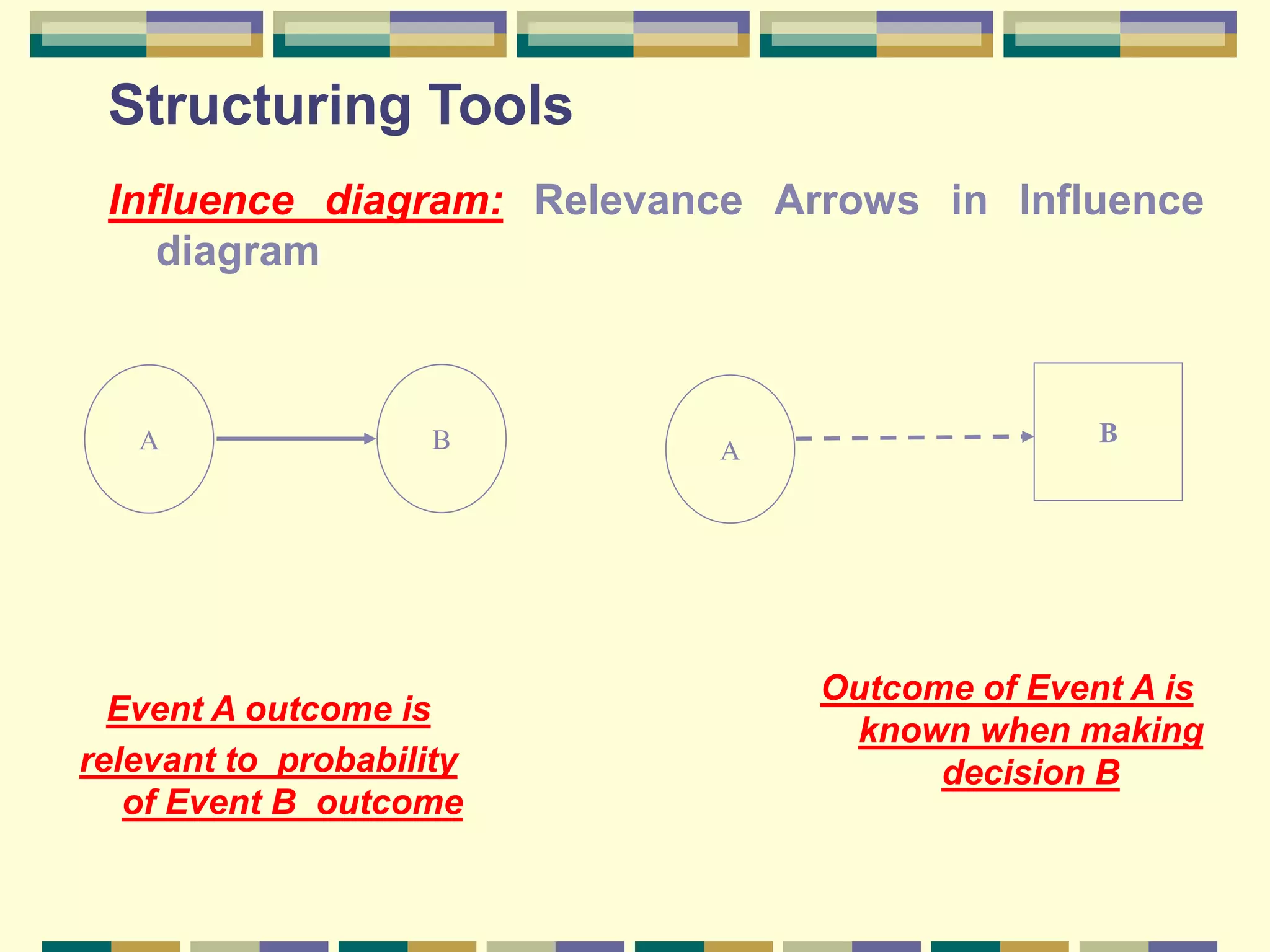
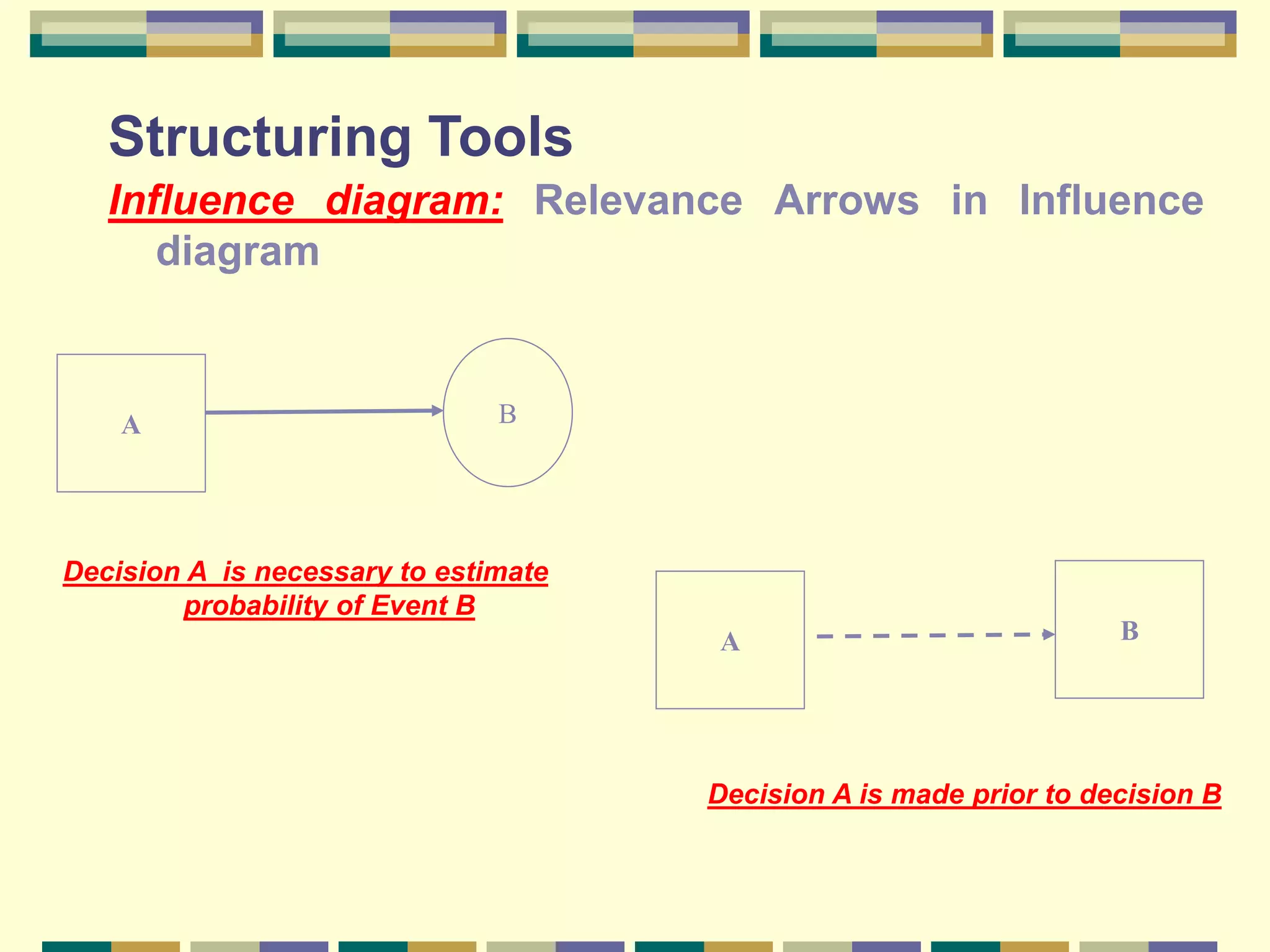
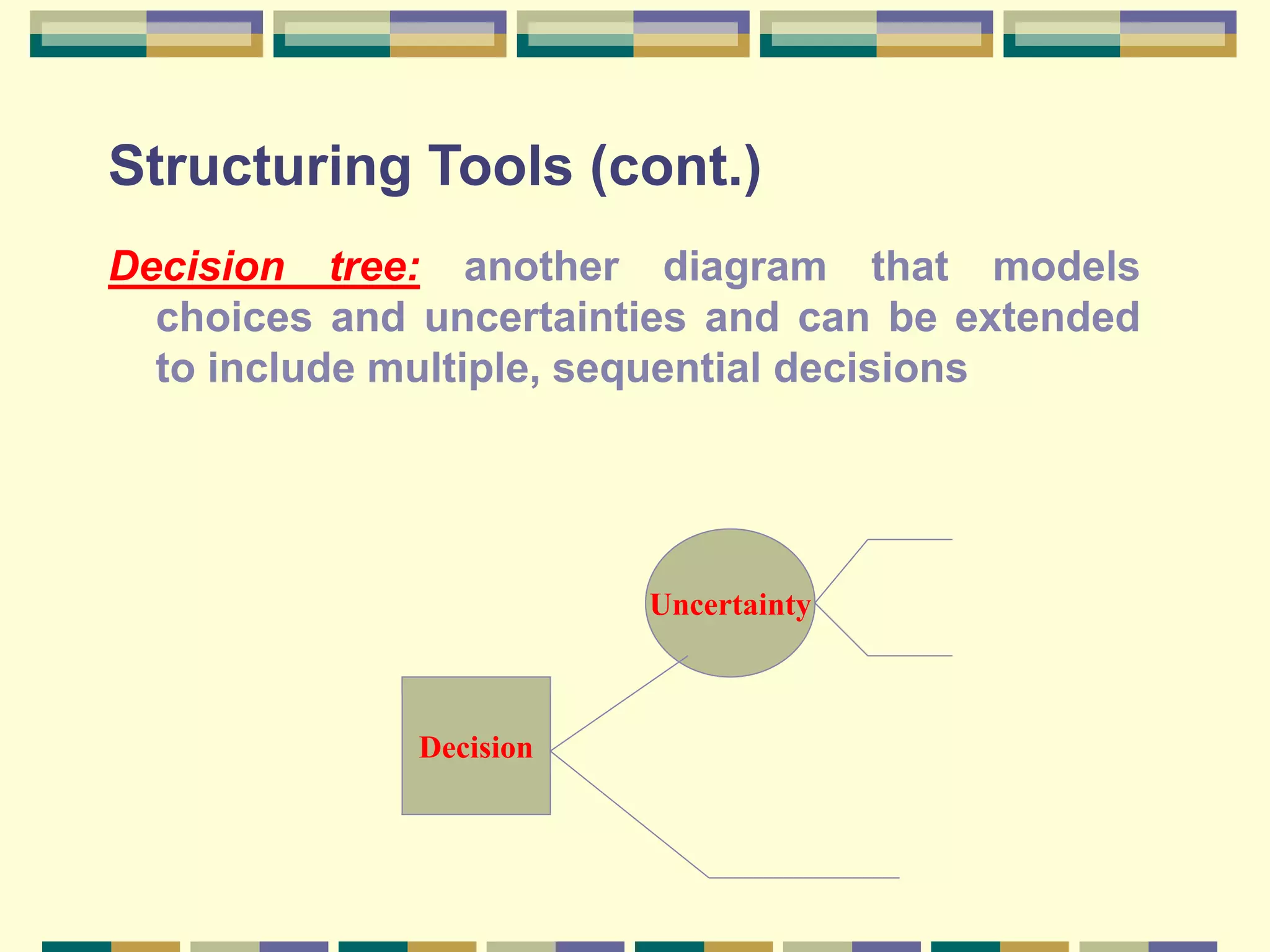
This chapter discusses modeling decision processes and decision support systems. It covers the typical modeling process of identifying a problem, analyzing requirements, and identifying variables and relationships. Common error in problem definition is premature focus on solutions rather than fully defining the problem. Tools for structuring problems include influence diagrams and decision trees. Probability can be estimated through frequency, subjectively, or through logic. Techniques for forecasting probabilities include direct estimation, odds forecasting, and comparison forecasting. Sensitivity analysis and value analysis are also discussed.

1. Chapter 4:
Modeling Decision Processes
Decision Support Systems in the 21st
Century, 2nd Edition
by George M. Marakas

2. 4-1: Modeling
Typical modeling process begins with identification
of a problem and analysis of the requirements of
the situation.
It is advisable to
 analyze the scope of the problem domain; and
 the forces and dynamics of the environment.

3. 4-1: Modeling
The next step is to identify the variables for the
model. The identification of decision variables
and their relationships is very important.
One should always ask if using a model is
appropriate??
If a model is appropriate, then one asks what
variables and relationships need to be specified,
using an appropriate modeling tool.

4. 4-1: Defining the Problem and Its Structure
A fully formed problem statement contains
three key components:
 The current state of affairs
 The desired state of affairs
 A statement of the central objective(s) that
distinguish the two

5. Problem Definition Errors
A common error: premature focus on the set
of solutions rather than the problem itself
The decision maker may be left with a solution
looking for a problem to solve
Failing to identify and define the problem fully may
result in a great solution that does not solve the
right problem

6. Problem Scope
The problem may be worth solving but the
scope is beyond the available resources or
time constraints
In such cases, the scope must be reduced to a
focus that allows a solution
One method to limit the scope is to identify its
breadth by asking questions about people
involved, cost and magnitude

7. Problem Structure
Design of problem structure is similar to design of
many other entities
 What is the final appearance?
 What are the elemental details?
 What are the relationships between those
elements?
Regardless of context, a problem structure can be
described in terms of choices, uncertainties and
objectives

8. Problem Structure (cont.)
Choices: there are always at least two
alternatives (one is “do nothing”)
Uncertainties: situations beyond the direct
control of the decision maker; their individual
probability of occurrence is only estimable within a
certain range
Objectives: methods of establishing the criteria
used to measure the value of the outcome

9. Structuring Tools
Influence diagram: a simple method of graphing the
components of a decision and linking them to show
the relationships between them
Decision
Objective
Uncertainty

10. Structuring Tools
Influence diagram: Relevance Arrows in Influence
diagram
B
Event A outcome is
relevant to probability
of Event B outcome
A B
A
Outcome of Event A is
known when making
decision B

11. Structuring Tools
Influence diagram: Relevance Arrows in Influence
diagram
A
Decision A is necessary to estimate
probability of Event B
B
B
Decision A is made prior to decision B
A

12. Structuring Tools (cont.)
Decision tree: another diagram that models
choices and uncertainties and can be extended
to include multiple, sequential decisions
Decision
Uncertainty

13. Common Decision Structures
Basic Risky Decision:
Decision maker takes a choice in the face of
uncertainty.
.
Success is a function of the choice and
outcome

14. Common Decision Structures
Certainty
A multiple-objective decision with little risk (risk
is not significant).
Multi-objective/multiple approach, no risk-
decision
Success is a function of the trade-off between
objectives.

15. Common Decision Structures
Sequential:
Decision process do not always present
themselves in a way that shows a clear
beginning and ending.
Conditions change over the time & choice made
earlier may no longer appropriate
Several risky decisions over time.
Earlier outcomes may affect later choices.

16. 4-2: Decision Models
Decision models can be classified in a number of
ways:
 Is time a factor? Models that do not include
time are “static” versus “dynamic”
 What is the technique’s mathematical focus?
 Some abstract model types are deterministic,
stochastic, simulation and domain specific

17. Model Classification Examples
Deterministic: linear programming, production planning
Stochastic: queuing theory, linear regression analysis

18. Model Classification Examples
Simulation: production modeling, transportation analysis
Domain-specific: EOQ, technology diffusion,
meteorological models

19. Conceptual Models
A formal mathematical approach is not always
appropriate
Conceptual models are formulated under the
notion that even though all problems are
unique, no problem is completely new
Decision makers can recall and combine a
variety of past experiences to create an accurate
model of the current situation

20. 4-3: Types of Probability
Three requirements of probability:
1. All probabilities are in the range 0 to 1
2. The probabilities of all outcomes of an event
must add up to the probability of their union
3. The total probability of a complete set of
outcomes must equal 1

21. How Are Probabilities Generated?
Long-run frequency: with enough “history”, you
can estimate an event’s probability by its relative
frequency
Subjective: probability represents an individual’s
“degree of belief” that an event will occur
Logic: a probability may be derivable, but its
accuracy may not be acceptable

22. 4-4: Techniques for Forecasting Probabilities
Direct probability forecasting — an expert is
simply asked to estimate the chance that an
outcome will occur
Odds forecasting — a series of bets are
proposed to determine how strongly the bettor
feels an event will occur
Comparison forecasting — similar to odds
forecasting except that one game has known
probabilities

23. Decomposing Complex Probabilities
Probabilities for complex events may be more
easily generated by using conditional
probabilities within subsets of the events
For example, it may be easier to forecast sales of a
weather-related product by forecasting sales under
good weather, then bad weather and then considering
the probability of bad weather

24. 4-5: Calibration and Sensitivity
A decision maker is said to be well calibrated if
his probability forecasts are correct at about
the same rate as his confidence in them (9
out of 10 times his 90% confidence intervals
should be correct).
Calibration requires years of experience and
feedback to develop.
Most of us are too optimistic and our intervals
are too tight.

25. Sensitivity Analysis
A method for testing the degree to which a set
of assumptions affects the results from a
model.
If a small change in the value of a variable
yields a measurable change in output, that
variable is said to be highly sensitive.
Variables that are not sensitive may be
treated as fixed, reducing the model’s
complexity.

26. Value Analysis
We always need to be concerned that enough
reliable information is available to make a
successful decision.
We can determine how much we are willing to
pay for better info by computing its expected
value.
This involves a comparison of the expected
return with the info to the expected return
without the info.