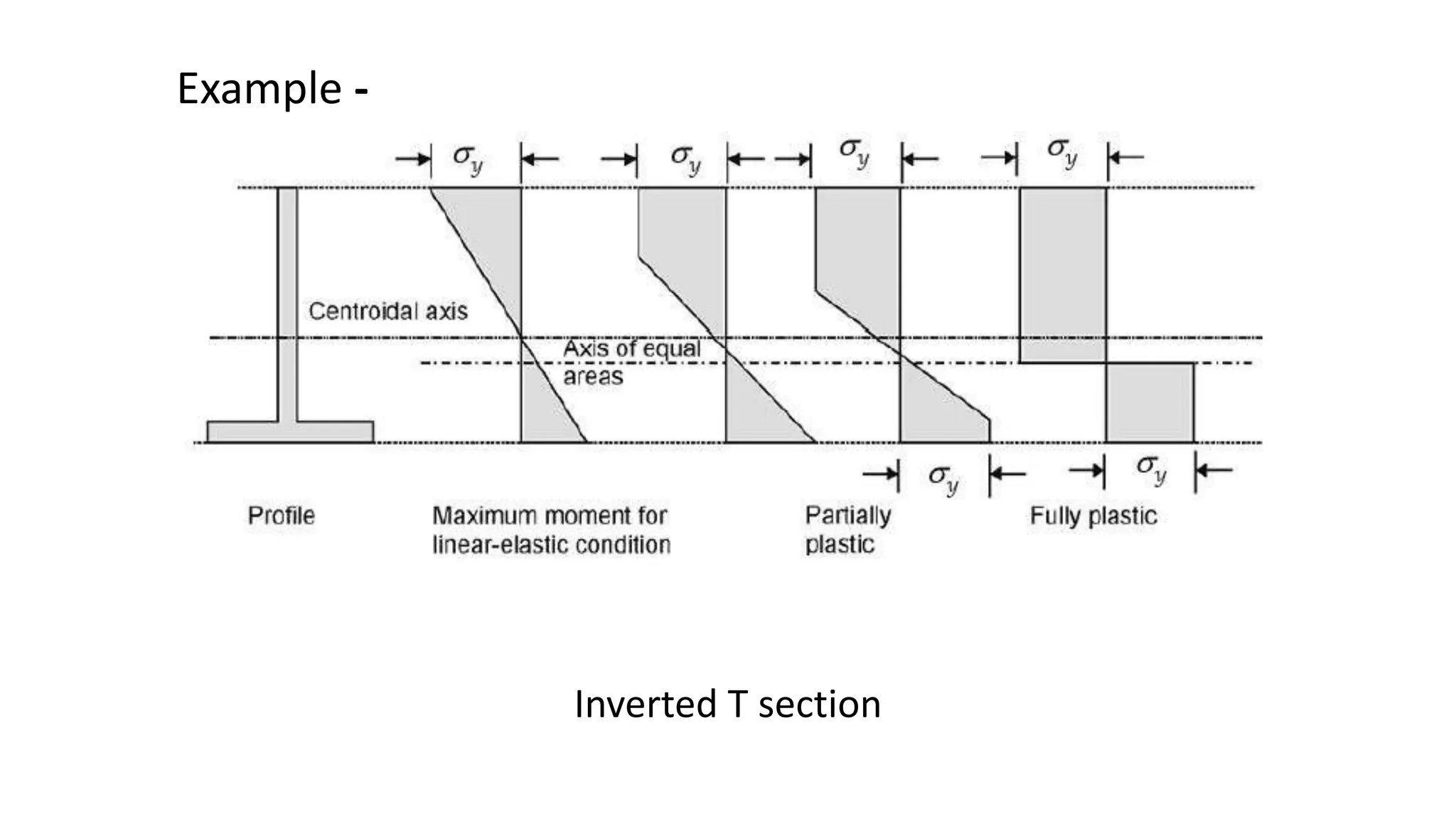
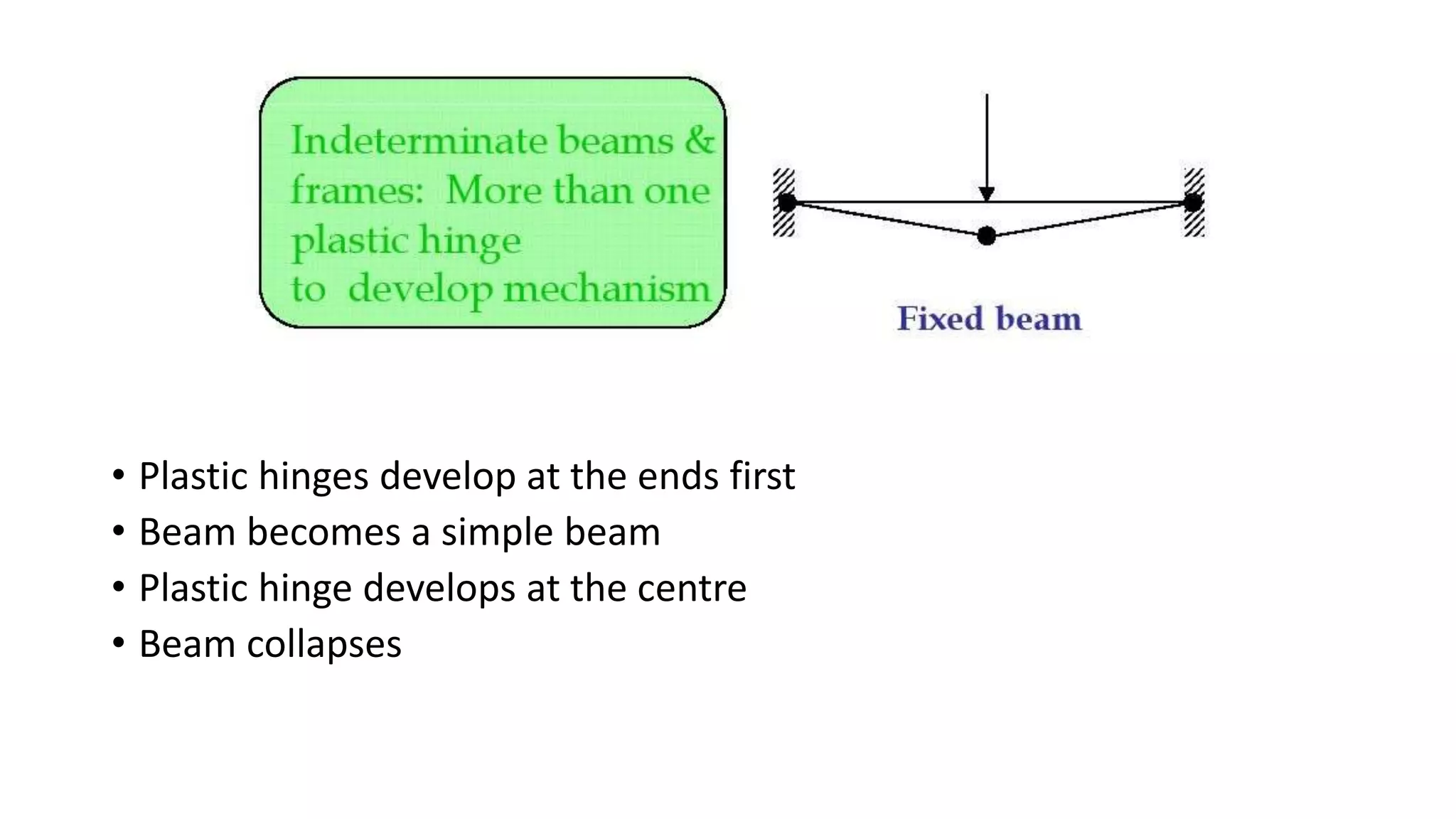
This seminar discusses plastic analysis, which is used to determine the collapse load of structures. It introduces key concepts like plastic hinges, which form at locations of maximum moment and allow large rotations. The plastic section modulus and shape factor are presented as ways to calculate the moment capacity of a fully yielded cross-section. Common collapse mechanisms like simple beams, fixed beams under uniform and point loads, and propped cantilevers are analyzed using the static method of plastic analysis or virtual work method. Determining collapse loads for various structural configurations is demonstrated through examples.

1. Seminar on
“Plastic Analysis”
By:
Shubham Satish Babar
Department of Civil Engineering
2015-16

2. 1) Introduction
2) Plastic hinge concept
3) Plastic section modulus & Shape factor
4) Collapse mechanism
5) Determination of collapse load
CONTENT-

3. Materials
1) Introduction -
•Elastic •Elastic-Perfectly plastic

4. Assumptions
•Plane sections remain plane in plastic condition
• Stress-strain relation is identical both in compression
and tension

5. Process of yielding of a section
•Let a cross-section increases gradually.
•Within elastic limit, M = σ .Z
•Z is section modulus, I/y
•Elastic limit –yield stresses reached
My = σ y.Z
•When moment is increased, yield spreads into inner When
moment is increased, yield spreads into inner fibres.
Remaining portion still elastic
• Finally, the entire cross-section yields

6. Change in stress distribution during yielding
Rectangular cross section
M<My M=My My<M<Mp M=Mp

7. Inverted T section
Example -

8. 2) Plastic hinge concept
•When the section is completely yielded, the section is fully plastic
• A fully plastic section behaves like a hinge – Plastic hinge
Plastic hinge is defined as an yielded zone due to bending in a
structural member, at which large rotations can occur at a section at
constant plastic moment, MP

9. Moment at which the entire section is under yield stress
3) Plastic section modulus & Shape factor -

10. Couple due to
Plastic Modulus
NA divides cross-section into 2 equal parts

11. Shape factor for various cross-sections

12. Circular section

13. Triangular section

14. I section

15. Beam mechanism -
4) Collapse mechanism -

16. • Plastic hinges develop at the ends first
• Beam becomes a simple beam
• Plastic hinge develops at the centre
• Beam collapses

17. • Plastic hinge develops at the fixed support first
• Beam becomes a simple beam
• Plastic hinge develops at the centre
• Beam collapses

18. Panel mechanism/sway mechanism

19. Gable Mechanism

20. Methods of Plastic Analysis
• Static method or Equilibrium method
Lower bound: A load computed on the basis of an assumed
equilibrium BM diagram in which the moments are not
greater than MP is always less than (or at the worst equal to)
the true ultimate load.
• Kinematic method or Mechanism method or Virtual work
Work performed by the external loads is equated to the
internal work absorbed by plastic hinges
Upper bound: A load computed on the basis of an assumed
mechanism is always greater than (or at the best equal to) the
true ultimate load.

21. The Plastic Hinges occur-
• At the point of maximum moment.
• At the connection involving change in geometry.
• Under the concentrated load.
• At the point of zero shear in span, loaded by uniformly
distribute load.

22. 5) Determination of collapse load -
1. Simple beam

23. • Virtual work method

24. 2. Fixed beam with UDL

25. Equilibrium :
Virtual Work :

26. 3. Fixed beam with point load

27. 4. Fixed beam with eccentric point load

28. Virtual Work :

29. 5. Propped cantilever with point load at
midspan

31. 6. Propped cantilever with UDL

33. REFERENCES -
• “Plastic Analysis” by Dr. Rajesh K. N. (Assistant Professor in Civil
Engineering Assistant Professor in Civil Engineering Govt. College of
Engineering, Kannur)
• Fundamentals of Structural Steel Design by M L Gambhir