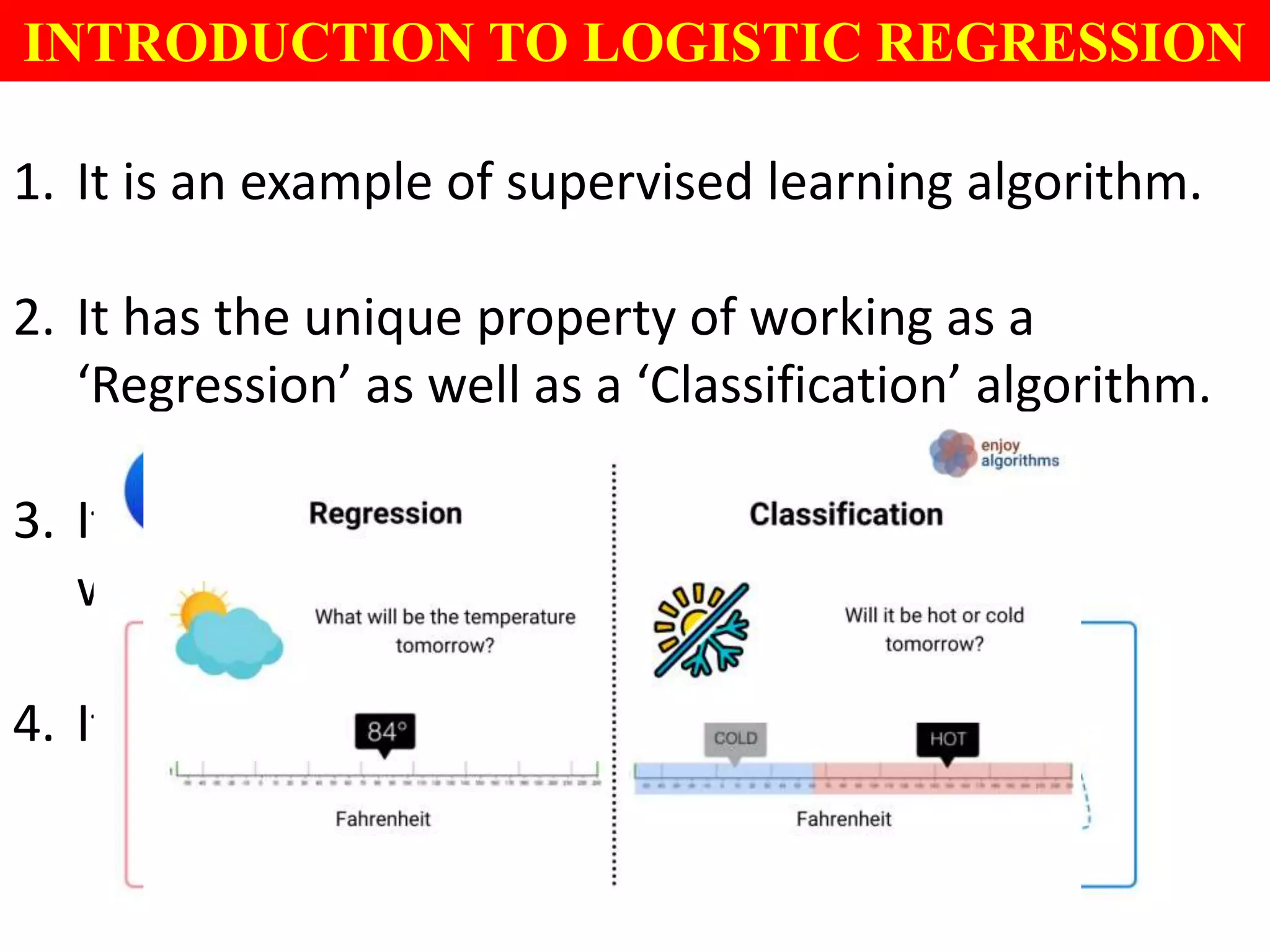
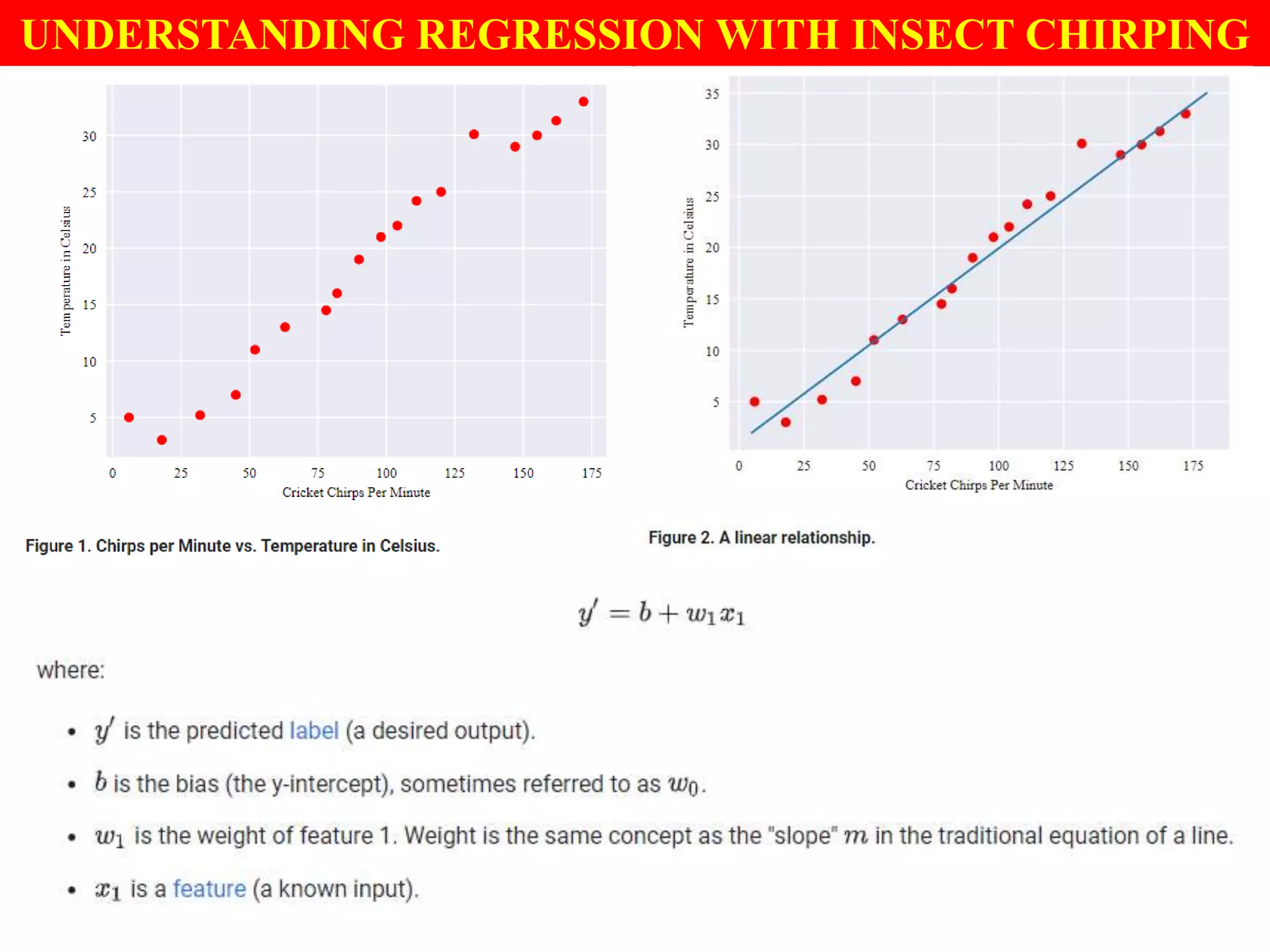
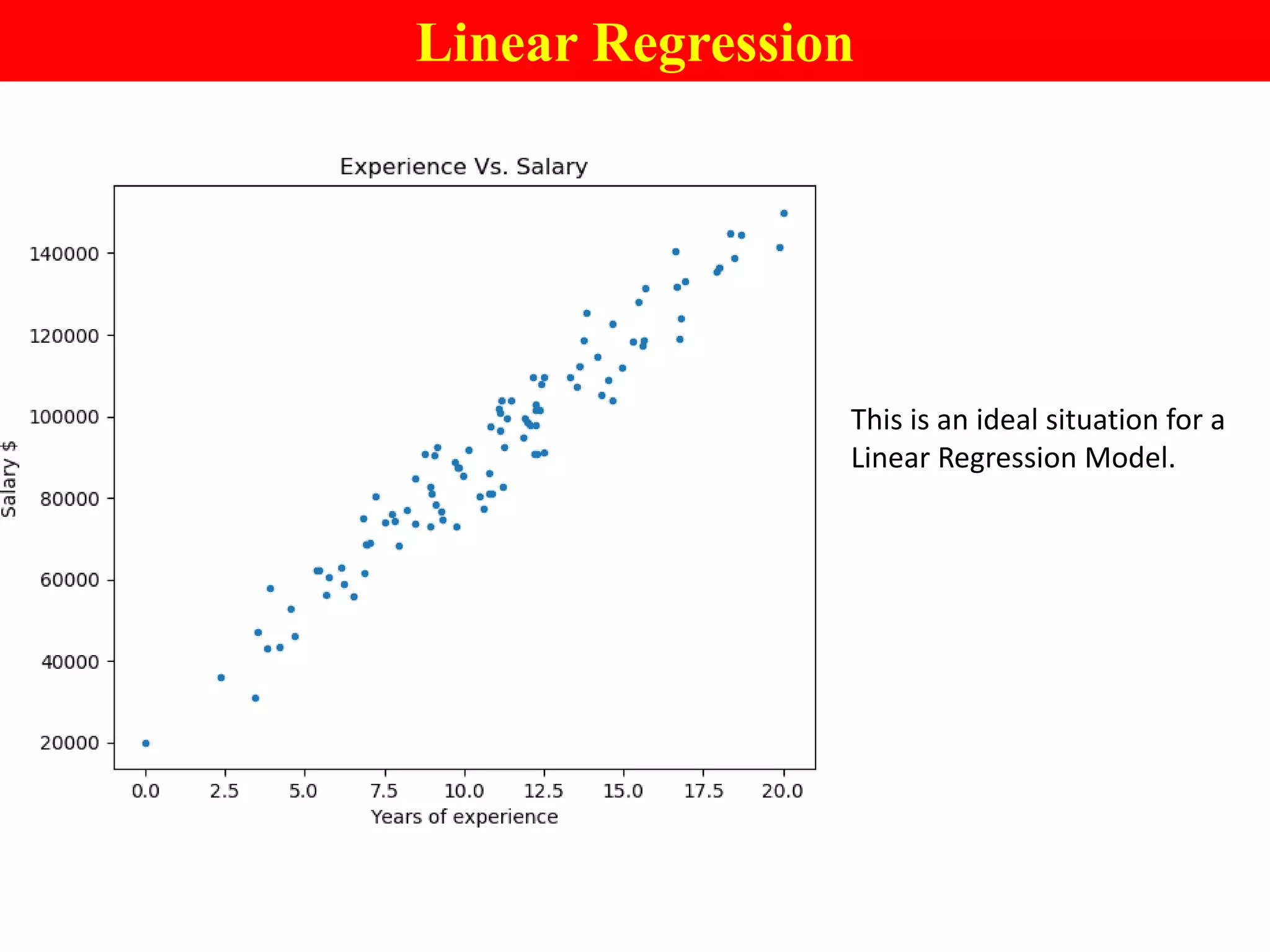
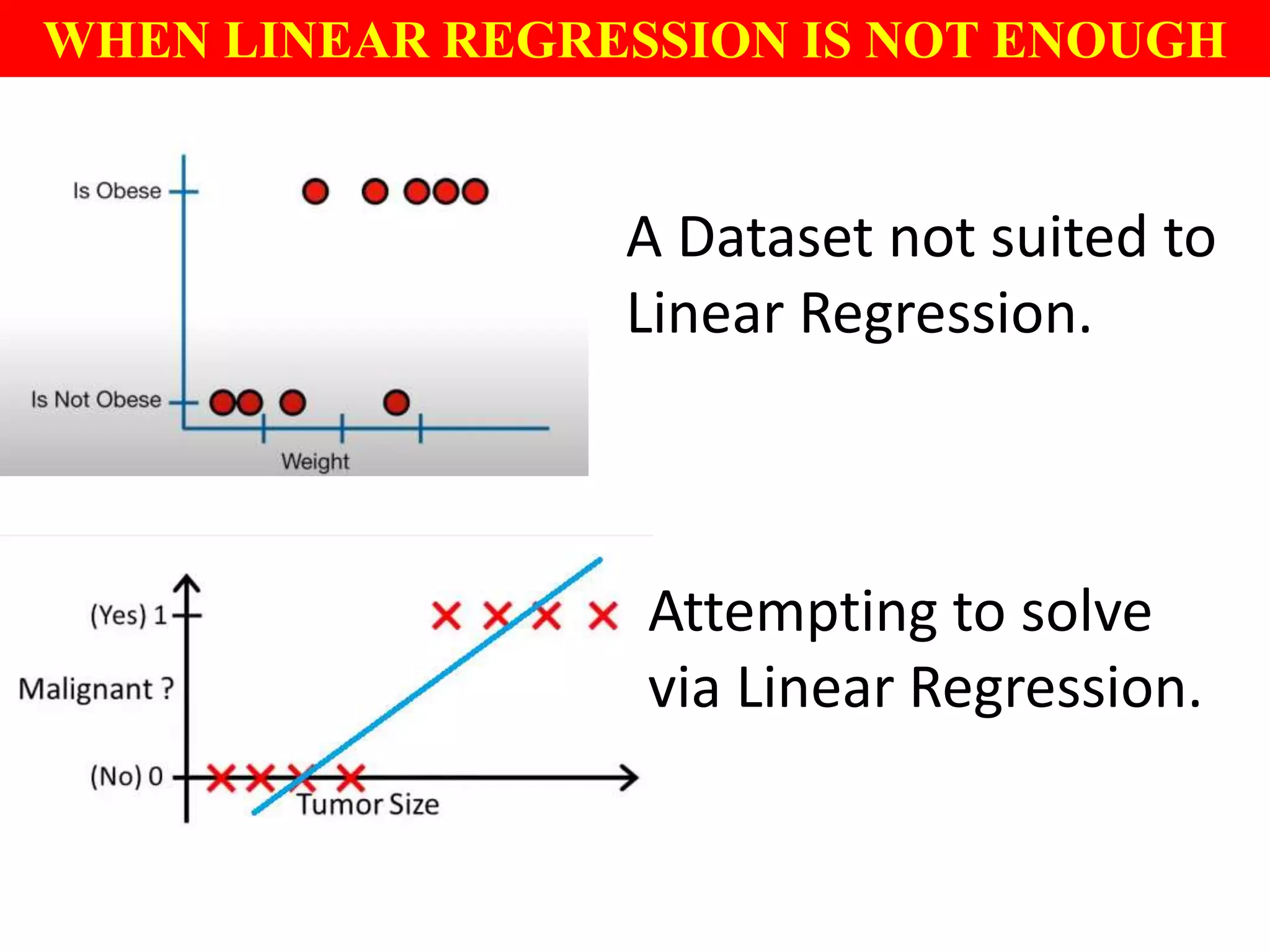
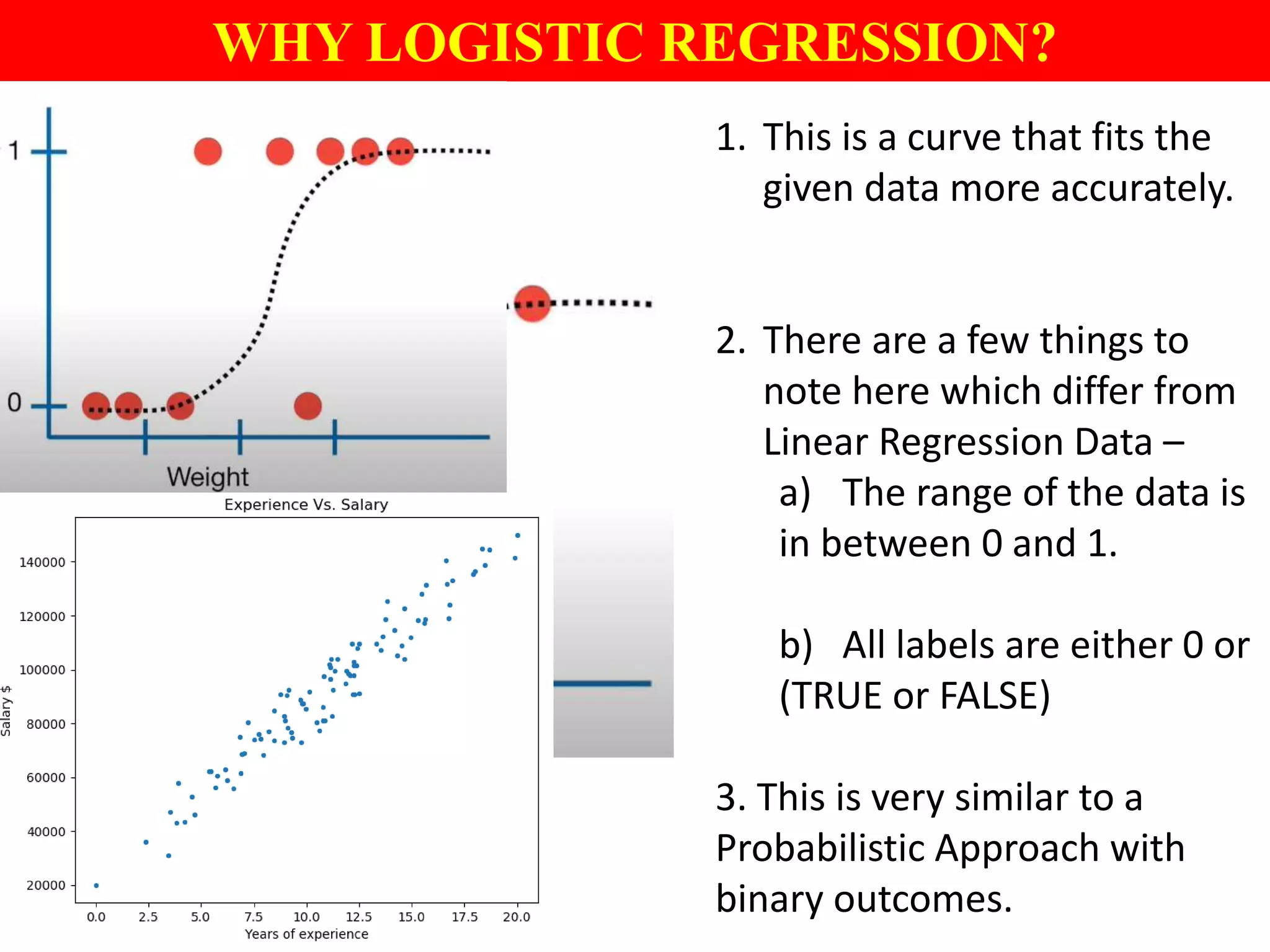
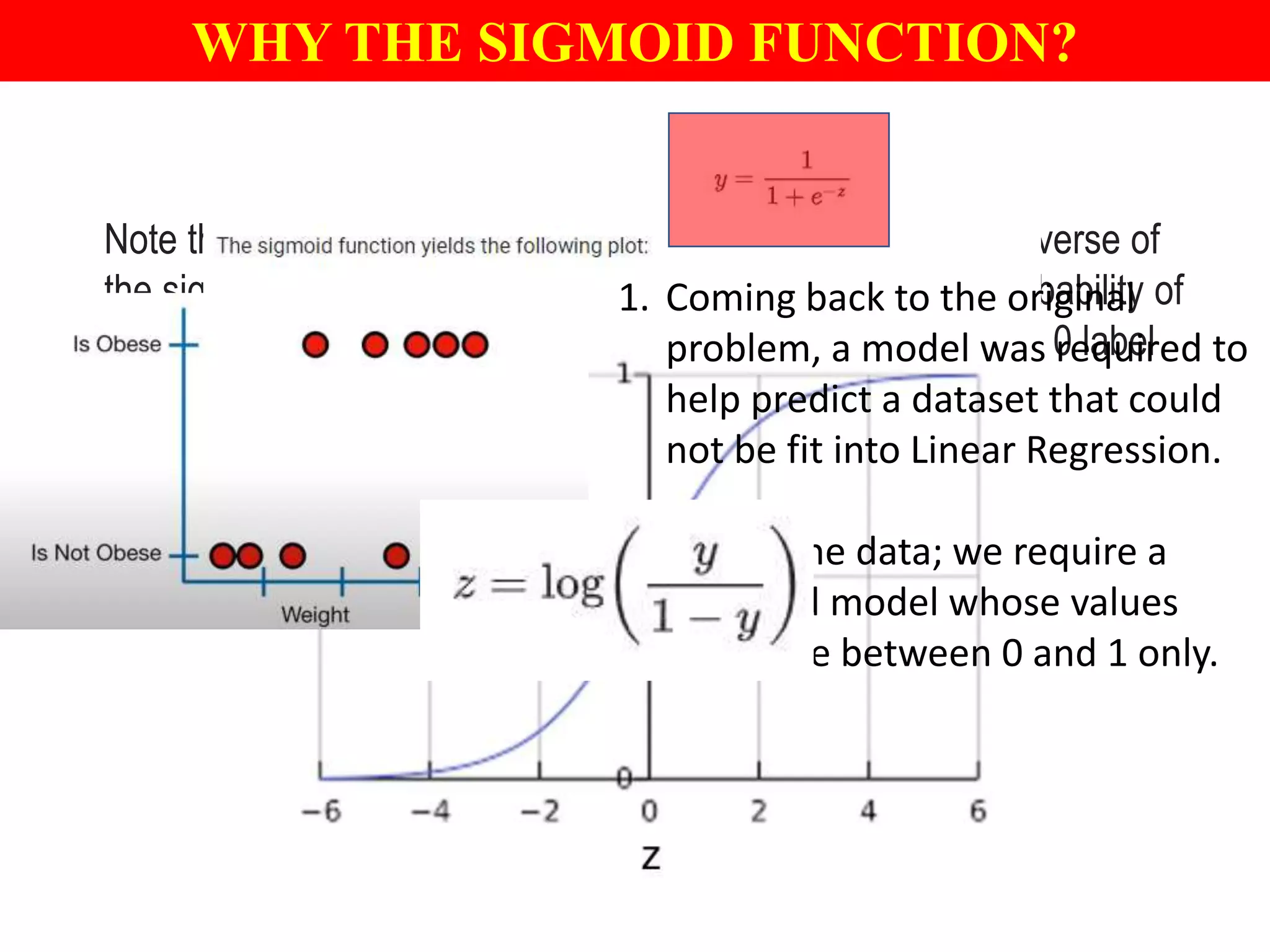
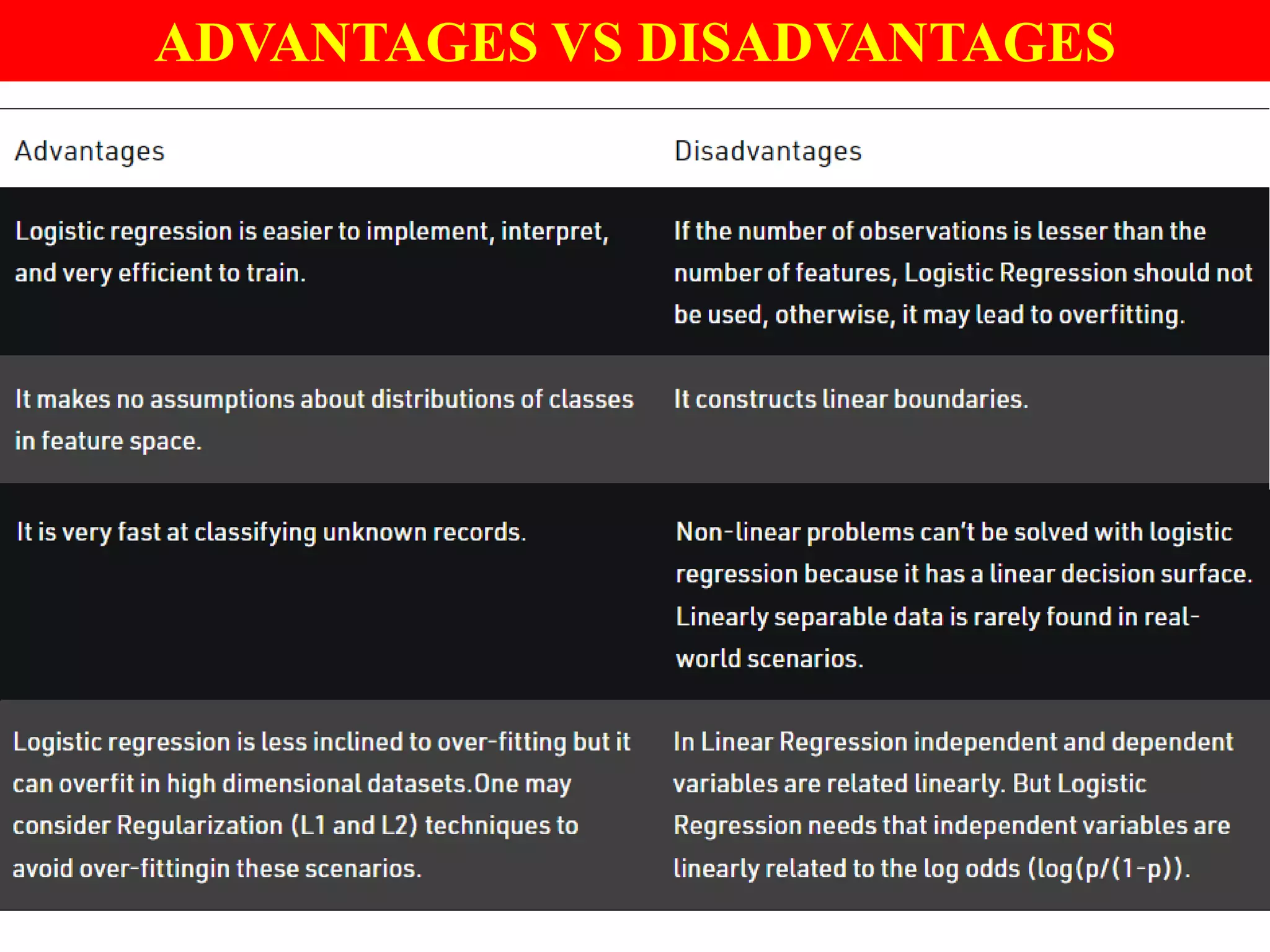
This document provides an introduction to logistic regression, including an overview of its key concepts and applications. Logistic regression can be used for classification problems where the dependent variable is binary. It uses a logistic function to model the probabilities of different outcomes. The loss function for logistic regression is log loss, as it aims to model binary classification probabilities between 0 and 1. Real-world examples of logistic regression include predicting customer purchases, detecting heart disease, and identifying fraudulent activities.

2. TABLE OF CONTENTS
Introduction to Logistic Regression
Understanding Regression
Need for Logistic Regression
The Mathematics
Example of Logistic Regression
Recap of Loss Function
Loss Function in Logistic Regression
Achieving Classification from Regression
Advantages and Disadvantages of Logistic Regression
Real World Examples of Logistic Regression

3. 1. It is an example of supervised learning algorithm.
2. It has the unique property of working as a
‘Regression’ as well as a ‘Classification’ algorithm.
3. It is used to predict data sets with or situations
which involve calculation of probabilities.
4. It is used for general binary classification.
INTRODUCTION TO LOGISTIC REGRESSION

4. LOGISTIC ‘REGRESSION’
Why is it called Logistic ‘REGRESSION’ ?
a technique for investigating the relationship
between independent variables or features
and a dependent variable or outcome

5. UNDERSTANDING REGRESSION WITH INSECT CHIRPING

6. Linear Regression
This is an ideal situation for a
Linear Regression Model.

7. WHEN LINEAR REGRESSION IS NOT ENOUGH
A Dataset not suited to
Linear Regression.
Attempting to solve
via Linear Regression.

8. WHY LOGISTIC REGRESSION?
1. This is a curve that fits the
given data more accurately.
2. There are a few things to
note here which differ from
Linear Regression Data –
a) The range of the data is
in between 0 and 1.
b) All labels are either 0 or
(TRUE or FALSE)
3. This is very similar to a
Probabilistic Approach with
binary outcomes.

9. The Math - Sigmoid Function (The Logistic Function)
1. A sigmoid function is a bounded, differentiable, real function that is
defined for all real input values and has a non-negative derivative at each
point and exactly one inflection point. A sigmoid "function" and a sigmoid
"curve" refer to the same object.
a) bounded – implies the value is bound from 0 to 1 or any other ‘x to y’
b) differentiable – it is continuous throughout.
c) non-negative derivative – function is only increasing ( as slope always
positive)
d) one inflection point – there exists only one point post which the graph
shows rapid increase

10. Note that z is also referred to as the log-odds because the inverse of
the sigmoid states that z can be defined as the log of the probability of
the 1 label (e.g., "dog barks") divided by the probability of the 0 label
(e.g., "dog doesn't bark"):
WHY THE SIGMOID FUNCTION?
1. Coming back to the original
problem, a model was required to
help predict a dataset that could
not be fit into Linear Regression.
2. Seeing the data; we require a
bounded model whose values
should lie between 0 and 1 only.

11. USING THE SIGMOID FN FOR LOGISTIC
REGRESSION

12. EXAMPLE OF LOGISTIC REGRESSION

13. RECAP OF LOSS FUNCTIONS
The Arrows represent the Respective Losses.
HIGH LOSS LOW LOSS
The commonly used Loss Function for Linear
Regression is the Mean Squared Loss Function.

14. LOSS FUNCTION IN LOGISTIC REGRESSION
The loss function of Logistic Regression is known
as the LOG LOSS

15. HOW TO CLASSIFY FROM REGRESSION?
To convert the regression output into a Classification Output,
we must define a Classification Threshold. If one half of the
regression output is one class, this is the value beyond which
the other class starts.

16. ADVANTAGES VS DISADVANTAGES

17. REAL WORLD EXAMPLES
The First Tennessee Bank in assosciation with IBM’s SPSS
(Statistical Package for the Social Sciences), also known as
IBM SPSS Statistics achieved increases upto 600% in cross-sale
campaigns using strategies developed through Logistic
Regression Models.

18. REAL WORLD EXAMPLES
Multiple models have been developed for Heart Disease
Prediction Using Logistic Regression. This is seen as a
simple classification problem of whether a person is more
prone to having a heart disease based on the medical
records (which are excellent datasets).

19. REAL WORLD EXAMPLES
Fraud detection: Logistic regression models can help teams
identify data anomalies, which are predictive of fraud.
Certain behaviors or characteristics may have a higher
association with fraudulent activities, which is particularly
helpful to banking and other financial institutions in
protecting their clients.