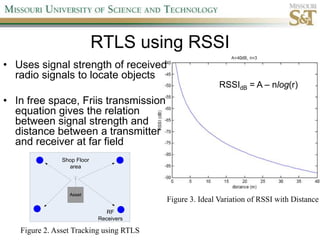
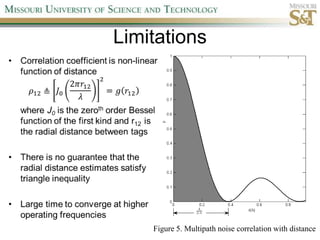
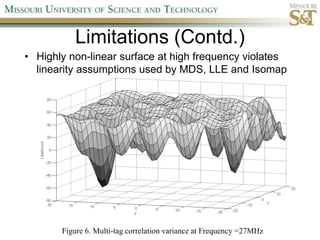
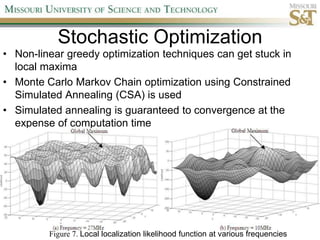
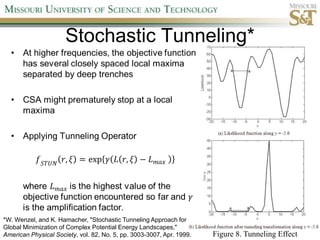
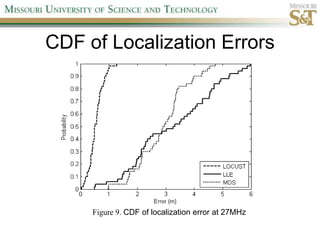
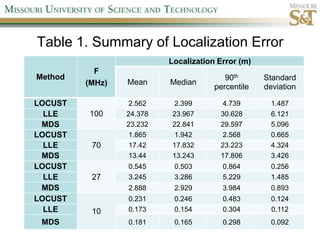
This document proposes a new localization algorithm called LOCUST that uses correlation coefficient estimates between pairwise wireless tags. It derives the probability distributions needed to estimate correlation coefficients and radial distances between tags. A cost function is defined incorporating these distributions and triangle inequality constraints. Constrained simulated annealing and a stochastic tunneling operator are used to optimize this non-linear, non-convex cost function. Simulation results show LOCUST has better localization accuracy than existing methods at high frequencies (>10MHz) but convergence time is still a concern.

1. Localization of Objects using Stochastic TunnelingMohammed Rana Basheer and S. JagannathanDepartment of Electrical and Computer Engineering, Missouri University of Science & Technology300 W 16th Street, Rolla, MO 65401mrbxcf@mst.edu, sarangap@mst.edu

2. Real Time Location System (RTLS)Used for locating or tracking assets in places where GPS signals are not readily availableUses Time of Arrival (ToA), Time Difference of Arrival (TDoA), Angle of Arrival (AoA) or Received Signal Strength Indicator (RSSI)Cost, accuracy and calibration issues have limited their adoption in factory environment. Figure 1. Boeing factory floor**http://www.ce.washington.edu/sm03/boeingtour.htm

3. RTLS using RSSIUses signal strength of received radio signals to locate objectsIn free space, Friis transmission equation gives the relation between signal strength and distance between a transmitter and receiver at far field RSSIdB = A – nlog(r)Figure 3. Ideal Variation of RSSI with DistanceFigure 2. Asset Tracking using RTLS

4. Limitations of RTLS using RSSIMultipath fading noise results in fast variation of received signal strengthBounded localization error only under Line of Sight (LoS) conditionShadow fading under LoSCostly periodic radio profiling required for Non-LoS conditionFigure 4. Localizing wireless tags in a room/container

5. Problem StatementA network of M wireless tags where the 3D coordinate of the ith tag is denoted by 𝜂𝑖=𝜂𝑖𝑥,𝜂𝑖𝑦,𝜂𝑖𝑧𝑇Anchor nodeshave perfect knowledge about their location while all other tags have imperfect a priori knowledge about their positionAll of them measure RSSI values from a common transmitter that is under NLoSconditionThe problem considered in this paper is to infer the true radial separation between tags from pair wise RSSI correlation coefficient estimates

6. Previous WorkNon-Parametric Methods treat the localization as a dimensionality reduction problem𝑃𝑖=𝑟𝑖1,𝑟𝑖2,⋯,𝑟𝑖𝐾𝑇∈𝑅𝐾->𝑋𝑖=𝑥𝑖,𝑦𝑖, 𝑧𝑖𝑇∈𝑅3Multi Dimensional Scaling (MDS)1Local Linear Embedding (LLE)2Isomap3 Yi Shang, Wheeler Ruml, Ying Zhang, and Markus P. J. Fromherz, “Localization from mere connectivity,” in Mobihoc ‘03, June 2003, pp. 201–212.N. Patwari and A. O. Hero, “Manifold learning algorithms forlocalization in wireless sensor networks,” in Proceedings of theIEEE International Conference on Acoustics, Speech and SignalProcessing (ICASSP), May 2004, volume 3, pp. 857–860. Wang C, Chen J, Sun Y, Shen X. Wireless sensor networks localization with Isomap. IEEE International Conference on Communications, 2009.

7. LimitationsCorrelation coefficient is non-linear function of distance𝜌12≜𝐽02𝜋𝑟12𝜆2=𝑔𝑟12 where J0 is the zeroth order Bessel function of the first kind and r12 is the radial distance between tagsThere is no guarantee that the radial distance estimates satisfy triangle inequalityLarge time to converge at higher operating frequencies Figure 5. Multipath noise correlation with distance

8. Limitations (Contd.)Highly non-linear surface at high frequency violates linearity assumptions used by MDS, LLE and IsomapFigure 6. Multi-tag correlation variance at Frequency =27MHz

9. Proposed IdeaLocalization problem is expressed as estimating the radial distance parameter between wireless tags using maximum-a-posteriori estimator Non-linear relationship between RSSI fading correlation coefficients and radial distance is used instead of linear approximations used in MDS, LLE and IsomapParameter estimation space is reduced by imposing triangular inequality constraintsFinally, the high convergence time arising due to uneven non-convex terrain of the localization cost function is improved by stochastic tunneling operator

10. StepsThe joint distribution of RSSI between a pair of co-located tags that are under NLoS condition with a common transmitter is derived to find the estimator for correlation coefficientLarge sample PDF of correlation coefficient estimator under NLoS conditions is derived to generate the localization cost functionFor a network with greater than 3 wireless tags, triangle inequality constraints are added to reduce the estimation spaceMonte Carlo Markov Chain optimization method called Constrained Simulated Annealing is used to solved this highly uneven cost function Finally, stochastic tunneling operator is applied to improve convergence speed

11. Joint PDF of Received Signal Strength Under NLoSJoint distribution of RSSI between two co-located wireless tags under NLoS is given by Downton’s Bivariate Exponential Distribution (DBED) as𝑓P𝑝12𝜇1,𝜇2,𝜌12=exp−𝑝1𝜇1+𝑝2𝜇21−𝜌12𝜇1𝜇21−𝜌12𝐼04𝜌12𝑝1𝑝21−𝜌122𝜇1𝜇2where p1,2 ={p1, p2} is the pair wise RSSI at wireless tags 1 and 2 respectively, μ1 and μ2 are their mean RSSI, ρ12 is the fading noise correlation between them and 𝐼⋅ is the zeroth order modified Bessel function of the first kind.

12. Estimating DBED Parameters𝜇1=1𝑁𝑖=1𝑁𝑝1𝑖, 𝜇2=1𝑁𝑖=1𝑁𝑝2𝑖, 𝜌12=𝑖=1𝑁𝑝1𝑖𝑝2𝑖𝑁𝜇1𝜇2−1, 𝜌12∗=0, 𝜌12<0𝜌12, 0≤𝜌12≤1&1, 𝜌12>1 where N is the pair-wise power sample size from which the above estimates are computedTo improve the accuracy of correlation coefficient estimate, Jackknife estimation technique is applied

13. PDF of Correlation Coefficient EstimateThe PDF of Jackknife estimation of multipath fading noise correlation coefficient for two co-located wireless tags under NLoS is given by𝑓𝜌𝜌12∗|𝑟12=1h𝑟12𝜙𝜌12∗−𝑔𝑟12h𝑟12Φ1−𝑔𝑟12h𝑟12+Φ𝑔𝑟12h𝑟12−1𝐼0,1𝜌12∗ where ηiis the 3D coordinate of ith tag, 𝜌12∗ is the correlation coefficient, 𝑔𝑟12=𝐸𝜌12, h𝑟12=𝑉𝑎𝑟𝜌12=3𝑔𝑟122+14𝑔𝑟12+3𝑁, N is the sample size, Φ⋅ and 𝜙⋅ are the CDF and PDF respectively of standard normal distribution.

14. Triangle Inequality ConstraintIf 𝑟𝑖𝑗, 𝑟𝑖𝑘and 𝑟𝑗𝑘represent the radial separation between tags i, j and k then 𝑟𝑖𝑗+𝑟𝑖𝑘−𝑟𝑗𝑘>0The metric for evaluating the violations isℶ𝑖𝑗𝑘=𝑟𝑗𝑘𝑟𝑖𝑗+𝑟𝑖𝑘1+𝑟𝑗𝑘−𝑟𝑖𝑗−𝑟𝑖𝑘:𝑟𝑗𝑘≥𝑟𝑖𝑘,𝑟𝑖𝑗Valid radial separations have ℶ𝑖𝑗𝑘≤1

15. Radial separation EstimationThe cost function of radial separation estimation from pair wise correlation coefficient measurements in a network of 𝑀≥3 wireless tags is given by𝐿𝑟,ξ =𝑙𝑟𝑖𝑗:𝑗>𝑖−𝑗>𝑖𝑘>𝑖𝑗≠𝑘𝜉𝑖𝑗𝑘ℶ𝑖𝑗𝑘−1where 𝑖,𝑗,𝑘𝜖{1,2,…,𝑀}, 𝑟𝑖𝑗 is the radial separation between ith and jth tag, ξijk ≥0 are Lagrange multipliers 𝑙𝑟𝑖𝑗:𝑗>𝑖= 𝜎𝑟−2𝑎−𝑀𝑀−1−1𝑖>𝑗𝑟𝑖𝑗Φ1−𝑔𝑟𝑖𝑗h𝑟𝑖𝑗+Φ𝑔𝑟𝑖𝑗h𝑟𝑖𝑗−1h𝑟𝑖𝑗, 𝜎𝑟 is the mode parameter for the Rayleigh prior distribution of 𝑟𝑖𝑗, a is the shape and 𝒃 is the scale parameters for the square root inverted gamma prior distribution of 𝜎𝑟

16. Stochastic OptimizationNon-linear greedy optimization techniques can get stuck in local maximaMonte Carlo Markov Chain optimization using Constrained Simulated Annealing (CSA) is usedSimulated annealing is guaranteed to convergence at the expense of computation timeFigure 7. Local localization likelihood function at various frequencies

17. Constrained Simulated Annealing*CSA is a variant of the popular Simulated Annealing (SA) optimizationGeneration function generates sample parameter values where the optimization objective function is evaluatedAcceptance function that depends on a parameter Tacc called the “Annealing Temperature” determines the probability of moving away from a local maximaCSA looks for saddle points (local maxima) that occur at the local maxima in radial distance space and local minima in Lagrange multiplier spaceSeparate acceptance functions for radial separation and Lagrange multiplier space to account for their different optimization objectives*B. W. Wah, Y. Chen, and T. Wang, "Simulated annealing with asymptotic convergence for nonlinear constrained optimization," J. of Global Optimization, Vol. 39, No. 1, pp. 1-37, Sep. 2007

18. Stochastic Tunneling*At higher frequencies, the objective function has several closely spaced local maxima separated by deep trenchesCSA might prematurely stop at a local maximaApplying Tunneling Operator𝑓𝑆𝑇𝑈𝑁𝑟,𝜉=exp𝛾𝐿𝑟,𝜉−𝐿𝑚𝑎𝑥 where 𝐿𝑚𝑎𝑥 is the highest value of the objective function encountered so far and 𝛾 is the amplification factor. *W. Wenzel, and K. Hamacher, "Stochastic Tunneling Approach for Global Minimization of Complex Potential Energy Landscapes," American Physical Society, vol. 82, No. 5, pp. 3003-3007, Apr. 1999.Figure 8. Tunneling Effect

19. Simulation Resultsm=20 wireless tags and n=4 anchor nodes in a 20m x 20m x 20m cubical workspaceAnchor nodes positioned at corners of this cubical workspaceWireless tags were distributed randomly in the cubical workspacecorrelation coefficient matrix was generated from double truncated normal random variables with mean and variance computed from N=100 pair wise RSSI samples and true radial separation between tags50 Monte Carlo simulation trials were performed to determine the mean, median, standard deviation and 90th percentile of localization errors.

20. CDF of Localization ErrorsFigure 9. CDF of localization error at 27MHz

21. Table 1. Summary of Localization Error

22. SummaryA novel localization algorithm calld LOCUST that uses correlation coefficient estimate between pair-wise wireless tags is presentedAt high frequencies (>10Mhz), MDS and LLE have very large localization errors due to their linearity assumption. At lower frequency (≤10MHz), tags are within the linear region of resulting in performance of all the algorithms within the same ballparkAs operating frequency increases accuracy of LOCUST degraded due to correlation coefficient estimates being very close to zeroConvergence time for LOCUST is a concern and better accuracy may be achieved with large computation time

23. Questions