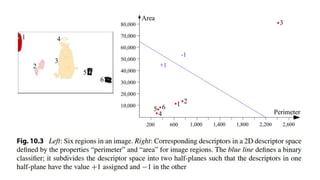
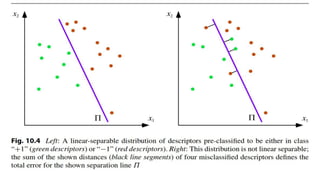
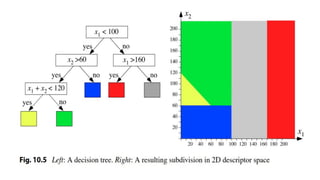
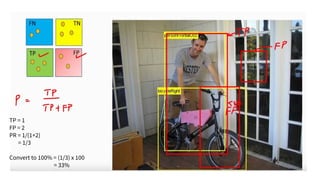
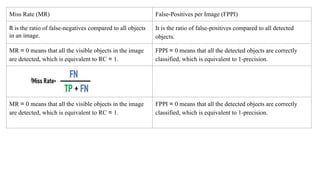
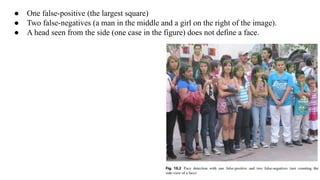The document discusses the fundamentals of object detection systems, detailing the processes of localization, classification, and evaluation. It explains descriptors, classifiers, and learning techniques, including supervised and unsupervised learning methods, along with performance evaluation metrics such as precision, recall, and accuracy. Additionally, the document emphasizes the importance of combining various learning approaches to enhance classifier performance in detecting objects.

1. Localization, Classification, and
Evaluation

2. Agenda
● Introduction
● Descriptors, Classifiers, and Learning
● Performance of Object Detectors

3. Three basic steps of an object detection system
● Localization
● Classification
● Evaluation
Object candidates are localized within a rectangular bounding box.
A bounding box is a special example for a region of interest.

4. ● Localized
○ Object candidates are mapped by classification either in detected objects or rejected candidates.
● Classification
○ Results should be evaluated within the system or by a subsequent performance analysis of the system.
true-positive / hit or a detection correctly detected object
false-positive / miss or a false detection detect an object where there is none
true-negative non-object regions are correctly identified as non-object regions
false-negative miss an object
Face Detected - Positive Case
Face Not Detected - Negative Case

6. ● One false-positive (the largest square)
● Two false-negatives (a man in the middle and a girl on the right of the image).
● A head seen from the side (one case in the figure) does not define a face.

7. Descriptors, Classifiers, and Learning
● Classification is defined by membership in constructed pairwise-disjoint classes being
subsets of Rn
for a given value n > 0.
● In other words, classes define a partitioning of the space Rn
.
● Time-efficiency is an important issue when performing classification.
● This subsection only provides a few brief basic explanations for the extensive area of
classification algorithms.

8. Descriptors
● A descriptor x = (x1
, . . . , xn
) is a point in an n-dimensional real space Rn
, called
descriptor space.
● A descriptor also called a feature.
● A feature in an image that, as commonly used in image analysis, combines a keypoint and
a descriptor.
● Thus, we continue to use “descriptor” rather than “feature” for avoiding confusion.
● It representing measured or calculated property values in a given order an illustration for
n = 2 (Eg: a SIFT descriptor is of length n = 128).
● Example: A descriptor x1
= (621.605, 10940) for Segment 1 in this descriptor space
defined by the properties “perimeter” and “area”.

10. Classifiers
● A classifier assigns class numbers to descriptors, typically, first, to a given set {x1
,
. . . , xm
} of already-classified descriptors for training (the learning set), and then to
the descriptors generated for recorded image/video data while being applied:
○ A (general) classifier assigns class numbers 1, 2, . . . , k for k > 1 classes and 0
for ‘not classified’.
○ A binary classifier assigns class numbers −1 and +1 in the cases where we are
only interested whether a particular event (Eg: ‘driver has closed eyes’) occurs,
specified by output +1.

11. ● A classifier is weak if it does not perform up to expectations (Eg: it might be just a
bit better than random guessing).
● Multiple weak classifiers can be mapped into a strong classifier, aiming at a
satisfactory solution of a classification problem.
● A statistical combination of multiple weak classifiers into one strong classifier.
● Weak or strong classifiers can be general-case (i.e. multi-class)
● classifiers or just binary classifiers; just being “binary” does not define “weak”.

12. Example 10.1 (Binary Classifier by Linear Separation
● A binary classifier may be defined by constructing a hyperplane Π : wT
x + b = 0
in Rn
for n ≥ 1.
● Vector w ∈ Rn
is the weight vector, and the real b ∈ R is the bias of Π.
● For n = 2 or n = 3, w is the gradient or normal orthogonal to the defined line or
plane, respectively.

13. ● One side of the hyperplane (including the plane itself) defines
the value “+1”, and the other side (not including the plane
itself) the value “−1”.
● Example for n = 2; the hyperplane is a straight line in this
case, and for n = 1, it is just a point separating R1
.
h(x) = wT
x + b
● The cases h(x) > 0 or h(x) < 0 then define the class values
“+1” or “−1” for one side of the hyperplane Π.

15. ● Such a linear classifier (i.e. defined by the weight vector w and bias b) can be calculated
for a distribution of (pre-classified) training descriptors in the n D descriptor space if the
given distribution is linear separable.
● If this is not the case, then we define the error for a misclassified descriptor x by its
perpendicular distance to the hyperplane Π.
d2
(x, Π) = |wT
x + b| / ǁwǁ2
● The task is to calculate a hyperplane Π such that the total error for all misclassified
training descriptors is minimized.
● This is the error defined in margin-based classifiers such as support vector machines and
is (usually) not explicitly used in AdaBoost.

16. Example 10.2 (Classification by Using a Binary Decision Tree)
● A classifier can also be defined by binary decisions at split nodes in a tree (i.e. “yes” or “no”).
● Each decision is formalized by a rule, and given input data can be tested whether they satisfy the rule
or not.
● Accordingly, we proceed with the identified successor node in the tree.
● Each leaf node of the tree defines finally an assignment of data arriving at this node into classes.
Example: Each leaf node can identify exactly one class in Rn
.
● The tested rules in the shown tree define straight lines in the 2D descriptor space.
● Descriptors arriving at one of the leaf nodes are then in one of the shown subsets of R2
.
● A single decision tree, or just one split node in such a tree, can be considered to be an example for a
weak classifier; a set of decision trees (called a forest) is needed for being able to define a strong
classifier.

18. Learning
● Learning is the process of defining or training a classifier based on a
set of descriptors; classification is then the actual application of the
classifier.
● During classification, we may also identify some mis-behaviour (e.g.
“assumed” mis-classifications), and this again can lead to another
phase of learning.
● The set of descriptors used for learning may be pre-classified or not.

20. Supervised Learning
● In supervised learning we assign class numbers to descriptors
“manually” based on expertise.
Example: “Yes, the driver does have closed eyes in this image”.
● As a result, we can define a classifier by locating optimized separating
manifolds in Rn
for the training set of descriptors.
● A hyperplane Π is the simplest case of an optimized separating
manifold.
● An alternative use of expert knowledge for supervised learning is the
specification of rules at nodes in a decision tree.
● This requires knowledge about possible sequences of decisions.

21. Unsupervised Learning
● In unsupervised learning we do not have prior knowledge about class memberships
of descriptors.
● When aiming at separations in the descriptor space, we may apply a clustering
algorithm for a given set of descriptors for identifying a separation of Rn
into
classes.
● Example: We may analyse the density of the distribution of given descriptors in Rn
;
● A region having a dense distribution defines a seed point of one class, and then we
assign all descriptors to identified seed points by applying, for example, the
nearest-neighbour rule.
● When aiming at defining decision trees for partitioning the descriptor space, we can
learn decisions at nodes of a decision tree based on some general data analysis
rules.
● The data distribution then “decides” about the generated rules.

22. Combined Learning Approaches
● There are also cases where we may combine supervised learning with
strategies known from unsupervised learning.
● Example: We can decide whether a given image window, also called
a bounding box, shows a pedestrian.
● This defines the supervised part in learning.
● We can also decide for a patch, being a subwindow of a bounding
box, whether it possibly belongs to a pedestrian.
● Example: The head of the cyclist is also considered to belong
possibly to a pedestrian.

23. ● When we generate descriptors for bounding boxes or patches (e.g.
measured image intensities at selected pixel locations),
● Then we cannot decide anymore manually for each individual
descriptor whether it is characteristic for a pedestrian or not.
● Example: for a set of given image windows, we know that they are
all parts of pedestrians, and the algorithm designed for generating a
classifier decides at some point to use a particular feature of those
windows for processing them further.

24. ● This particular feature might not be generic in the sense that it
separates any window showing a part of a pedestrian from any
window showing no part of a pedestrian.
● Such an “internal” mechanism in a program that generates a classifier
defines an unsupervised part in learning.
● The overall task is to combine available supervision with
unsupervised data analysis when generating a classifier.

26. Performance of Object Detectors
● Object Detector → Applying a classifier for an object detection problem.
● Evaluations of designed object detectors are required to compare their performance under particular conditions.
● There are common measures in pattern recognition or information retrieval for performance evaluation of
classifiers.

27. ● TP = 12, FP = 1, and FN = 2, TN = None
● In this figure doesn’t indicate how many
non-object regions have been analysed and
correctly identified as being no faces.
● We can’t specify the number TN.
● We need to analyse the applied classifier for
obtaining TN.
● Thus, TN is not a common entry for performance
measures.

28. Precision (PR) Recall (RC)
It is the ratio of true-positives compared to all
detections.
Itis the ratio of true-positives compared to all potentially
possible detections
PR = 1, termed 1-precision, means that no
false-positive is detected.
RC = 1 means that all the visible objects in an image are
detected and that there is no false-negative.

29. TP = 1
FP = 2
PR = 1/(1+2)
= 1/3
Convert to 100% = (1/3) x 100
= 33%

30. Miss Rate (MR) False-Positives per Image (FPPI)
It is the ratio of false-negatives compared to all objects
in an image.
It is the ratio of false-positives compared to all detected
objects.
MR = 0 means that all the visible objects in the image
are detected, which is equivalent to RC = 1.
FPPI = 0 means that all the detected objects are correctly
classified, which is equivalent to 1-precision.
MR = 0 means that all the visible objects in the image
are detected, which is equivalent to RC = 1.
FPPI = 0 means that all the detected objects are correctly
classified, which is equivalent to 1-precision.

31. True-Negative Rate (TNR) Accuracy (AC)
It is the ratio of true-negatives com-
pared to all decisions in “no-object” regions.
It is the ratio of false-positives compared to all detected
objects.
MR = 0 means that all the visible objects in the image
are detected, which is equivalent to RC = 1.
The accuracy is the ratio of correct decisions compared to all
decisions.
We are usually not interested in numbers of true-negatives, these two measures have less significance in performance
evaluation studies.