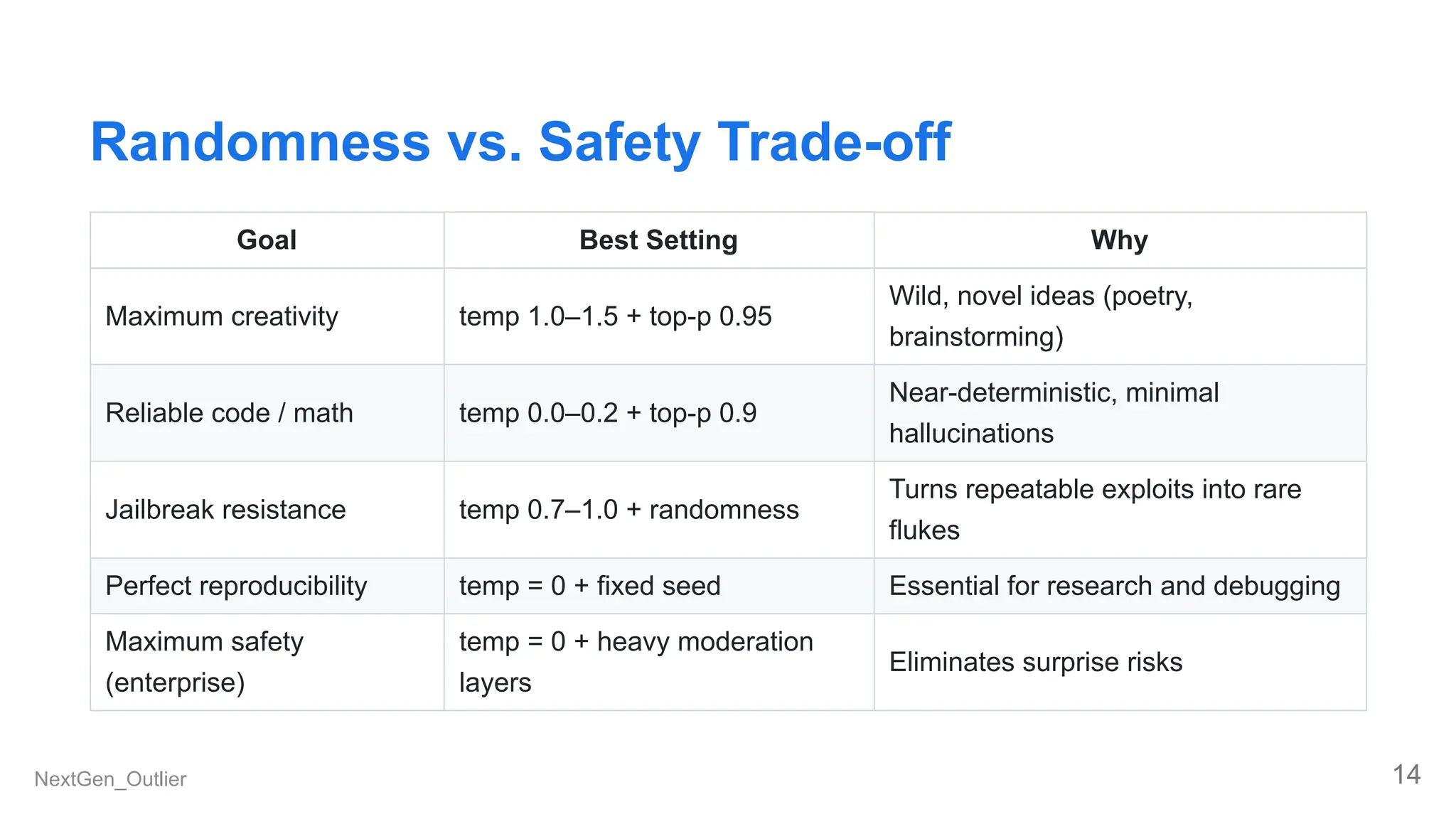
Many people perceive the varying responses from ChatGPT, Claude, or Grok as bugs. However, these variations are intentional, mathematically grounded features that stem from decades of randomized algorithm design, including concepts like Monte Carlo, Las Vegas, quicksort pivots, Miller-Rabin, dropout, and adversarial robustness. If you've ever wondered about the following: - Why LLMs change their mind on the same prompt - Why a temperature setting greater than 0 can sometimes be the safest choice - Why an average accuracy of 95% is insufficient when facing adversaries This discussion is for you. https://lnkd.in/eztWcawe

1. Are Large Language Models Randomized
Algorithms?
Exploring Randomness, Adversaries, and Robustness
By - Tamanna
NextGen_Outlier 1

2. LLMs Have a Curious Habit
Ask the exact same question twice → you might get two different answers
Traditional programs are deterministic:
2 + 2 → always 4
sort([3,1,4,1,5]) → always [1,1,3,4,5]
LLMs behave differently on purpose
→ This unpredictability is not a bug — it is a feature built on randomness
NextGen_Outlier 2

3. Randomness = The Secret Sauce
When an LLM writes a story or explains physics:
No single “correct” answer is hardcoded
It learned a probability landscape over billions of tokens
At generation time → it spins a weighted roulette wheel
Even during training: data shuffling, random weights, dropout, mini-batches
→ LLMs live and breathe randomness from day one
Conclusion: LLMs are randomized algorithms in the strict CS sense
NextGen_Outlier 3

4. Roadmap
1. Classic randomized algorithms (Monte Carlo & Las Vegas)
2. Real-world examples from sorting, graphs, geometry, crypto
3. How LLMs use randomness (training + inference)
4. Why randomness is required: adversaries
5. Why average accuracy isn’t enough
6. Closing thought: the most sophisticated randomized algorithms ever built
NextGen_Outlier 4

5. What Are Randomized Algorithms?
Use chance (coin flips, lottery) to make decisions
Aspect Deterministic Randomized
Output for same input Always the same Can vary
Correctness 100% guaranteed High probability
Use case Exact solutions Speed, robustness, approximation
Classic example Binary search Quicksort with random pivot
Two families:
Monte Carlo → fixed time, small error chance
Las Vegas → always correct, variable time
NextGen_Outlier 5

6. Monte Carlo Classic: Approximating π
import random
def approx_pi(n):
inside = 0
for _ in range(n):
x, y = random.random(), random.random()
if x*x + y*y <= 1: inside += 1
return 4 * inside / n
print(approx_pi(10000)) # → ~3.1376, 3.142, 3.1401…
NextGen_Outlier 6

7. How it works (step by step):
Imagine a square from (0,0) to (1,1) with a quarter-circle inside.
Throw thousands of random "darts" (points) into the square.
Count how many land inside the circle.
π ≈ 4 × (points inside circle) / (total points thrown)
Each run gives a slightly different answer, classic Monte Carlo: fast, approximate, high-probability
correctness.
NextGen_Outlier 7

8. Las Vegas Classic: BogoSort (the worst &
funniest)
import random
def is_sorted(arr):
return all(arr[i] <= arr[i+1] for i in range(len(arr)-1))
def bogosort(arr):
while not is_sorted(arr):
random.shuffle(arr)
return arr
# Warning: Expected time O(n!) only use on tiny lists!
How it works:
Keep shuffling the array completely at random.
After each shuffle, check if it's sorted.
Stop only when it is (which might take forever).
Pure Las Vegas: always correct, but time varies wildly. Perfectly illustrates the trade-off.
NextGen_Outlier 8

9. Quicksort with Random Pivot
import random
def quicksort(arr):
if len(arr) <= 1: return arr
pivot = random.choice(arr)
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
print(quicksort([3,1,4,1,5,9,2,6,5,3,5]))
# → [1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]
NextGen_Outlier 9

10. Why random pivot?
Without randomness: worst case O(n²) on already-sorted data.
With random pivot: expected O(n log n), robust against adversarial inputs.
Step-by-step process:
If array has 0–1 elements → done.
Pick a completely random element as pivot.
Partition into: less than pivot, equal, greater than pivot.
Recursively sort left and right parts.
Combine results
NextGen_Outlier 10

11. Miller-Rabin: The Monte Carlo That Secures the
Internet
Used in cryptography (RSA, banking, WhatsApp)
Core idea:
To test if a huge number is prime.
Pick random bases and run a mathematical "witness" test.
If it fails once → definitely composite.
If it passes many times → "probably prime" with extremely low error.
Run 40 rounds → chance of error smaller than being struck by lightning.
Real-world Monte Carlo success story.
NextGen_Outlier 11

12. LLMs as Randomized Algorithms
LLMs predict the next token using a probability distribution over the vocabulary.
At inference time: instead of always picking the most likely token, they sample — just like throwing
weighted dice.
Sources of randomness:
Training: Stochastic gradient descent, data shuffling, random initialization, dropout
Inference: Temperature > 0, top-k, top-p sampling
Result → non-deterministic, creative, robust outputs
LLMs are fundamentally Monte Carlo algorithms for generating coherent text.
NextGen_Outlier 12

13. Advanced Sampling Techniques
Modern LLMs use more than just temperature:
Top-k sampling: Only consider the k most likely tokens (e.g., k=50)
Top-p (nucleus) sampling: Keep the smallest set of tokens whose total probability ≥ p (usually 0.9–0.95)
Why?
Prevents the model from ever picking truly absurd low-probability tokens while preserving diversity and
creativity.
Process:
Start with full probability distribution.
Apply temperature to make it flatter/sharper.
Trim using top-k or top-p.
Sample from the reduced set.
NextGen_Outlier 13

14. Randomness vs. Safety Trade-off
Goal Best Setting Why
Maximum creativity temp 1.0–1.5 + top-p 0.95
Wild, novel ideas (poetry,
brainstorming)
Reliable code / math temp 0.0–0.2 + top-p 0.9
Near-deterministic, minimal
hallucinations
Jailbreak resistance temp 0.7–1.0 + randomness
Turns repeatable exploits into rare
flukes
Perfect reproducibility temp = 0 + fixed seed Essential for research and debugging
Maximum safety
(enterprise)
temp = 0 + heavy moderation
layers
Eliminates surprise risks
NextGen_Outlier 14

15. Why Randomness Defends Against Adversaries
Deterministic model:
→ One perfect jailbreak prompt works every single time
Randomized model:
→ Same prompt only succeeds with probability p (e.g., 10%)
→ Attacker can’t reliably exploit
Process:
Adversary crafts malicious prompt
Model processes it
With randomness → most outputs are safe/refusals
Only rare unlucky rolls leak harmful content
Randomness turns repeatable attacks into occasional flukes
NextGen_Outlier 15

16. Why Average Accuracy Isn’t Enough
An LLM might score 95% on benchmarks → sounds impressive
But the remaining 5% can contain consistent, repeatable failures on specific inputs
Adversaries don’t care about your average - they search for and exploit your worst-case behavior
In high-stakes domains (medicine, law, security), one repeatable failure is catastrophic
NextGen_Outlier 16

17. Who Is the Adversary?
Not just evil hackers:
Malicious users → crafting jailbreak prompts
Innocent edge cases → biased data, rare queries
Red-team testers → ethical attackers improving safety
Automated systems → other LLMs probing for weaknesses
All force us to design for worst-case robustness, not just average performance
NextGen_Outlier 17

18. Stochastic Training & Probabilistic Guarantees
Randomness starts long before inference:
SGD: Random mini-batches, shuffling, weight init → helps escape bad minima
Dropout: Randomly disables neurons → trains thousands of sub-networks (Monte Carlo ensemble)
Modern evaluation uses the same language as classic randomized algorithms:
pass@k: Chance of ≥1 correct answer in k samples
best-of-N: Generate N outputs, pick the best
Same ideas as repeating Miller–Rabin or Karger’s algorithm!
NextGen_Outlier 18

19. Final Thought
LLMs are not buggy deterministic programs that happen to be inconsistent
They are the most advanced randomized algorithms ever created
They inherit:
Speed through approximation
Robustness against adversarial inputs
Ability to explore vast creative spaces
But they also carry the responsibility:
→ We can only promise overwhelming probability, never absolute certainty
Randomness isn’t a side effect. It is the secret ingredient that allows LLMs to exist, improve, and survive
in a messy, adversarial world
NextGen_Outlier 19

20. Thank You!
NextGen_Outlier 20