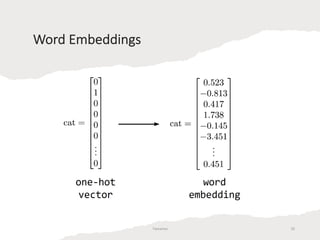
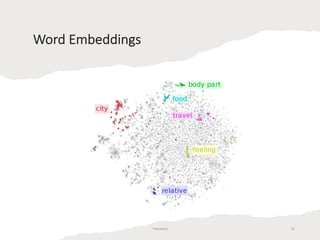
Embeddings are generally better than TF-IDF features for several reasons. TF-IDF represents words as high-dimensional, sparse vectors based on word counts, but embeddings represent words as low-dimensional, dense vectors that encode semantic relationships between words. Embeddings reduce dimensionality and computation costs compared to TF-IDF while capturing similarities between related words. While TF-IDF assumes words are independent, embeddings place similar words in close proximity in vector space.

1. Why do embeddings (Usually) better than TF-IDF
Features?
Tamanna 1

2. Index
• Why?
• TF-IDF
• Embedding
• Comaprision
Tamanna 2

3. Why?
Tamanna 3

4. Vector Representation
• We define a word by a vector of counts over contexts
oEach word is associated with a vector of dimension |V|
oWe expect similar words to have similar vectors
oGiven the vectors of two words, we can determine their similarity
Tamanna 4

5. Vector Representation
Raw counts are problematic:
o frequent words will characterize most words -> not informative
Except from raw counts, we can use other functions:
o Pointwise Mutual Information (PMI)
o TF-IDF
Tamanna 5

6. From Sparse to Dense
• These vectors are:
o huge – each of dimension |V|
o sparse – most entries will be 0
• We want our vectors to be small and dense:
o Use a reduction algorithm over a matrix of sparse vectors
o Learn low-dimensional word vectors directly -usually referred as
“word embeddings”
Tamanna 6

7. TFIDF
• TF(t) = (Number of times term t appears in a document) / (Total
number of terms in the document)
• IDF(t) = log_e(Total number of documents / Number of documents
with term t in it + 1)
• long (length |V|= 20,000 to 50,000)
• sparse (most elements are zero)
Tamanna 7

8. Limitations of TF-IDF
• It computes document similarity directly in the word-count space,
which may be slow for large vocabularies
• Large memory and expensive computation because the vectors are
long
• It assumes that the counts of different words provide independent
evidence of similarity
• It makes no use of semantic similarities between words
Tamanna 8

9. Embedding
• Each word in the vocabulary is represented by a low dimensional vector
• All words are embedded into the same space
• Similar words have similar vectors = their vectors are close to each other in
the vector space
• In one-hot vector representation, a word is represented as one large sparse
vector
• Instead, word embeddings are dense vectors in some vector space
word vectors are continuous representations of words
vectors of different words give us information about the potential
relations between the words - words closer together in meaning have
vectors closer to each other
Tamanna 9

10. Word Embeddings
Tamanna 10

11. Word Embeddings
“Representation of words in continuous space”
Inherit benefits
• Reduce dimensionality
• Semantic relatedness
• Increase expressiveness
oOne word is represented in the form of several features (numbers)
Tamanna 11

12. Word Embeddings
Tamanna 12

13. In summary:
Tamanna 13

14. References
Tamanna 14
• https://towardsdatascience.com/natural-language-processing-
feature-engineering-using-tf-idf-e8b9d00e7e76
• https://towardsdatascience.com/tf-idf-for-document-ranking-from-
scratch-in-python-on-real-world-dataset-
796d339a4089#:~:text=TF%2DIDF%20stands%20for%20%E2%80%9C
Term,Information%20Retrieval%20and%20Text%20Mining.
• https://miro.medium.com/max/4800/1*tKk9S7v_kxYLj7Sj-
VnTkg.jpeg
• https://ruder.io/word-embeddings-1/
• https://medium.com/@arihantjain25121995/word-embeddings-
using-bow-tf-idf-with-an-example-a10d2e2ab03e

15. Thank you for your attention!
Tamanna 15