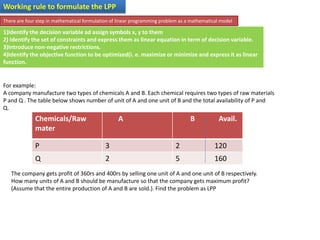
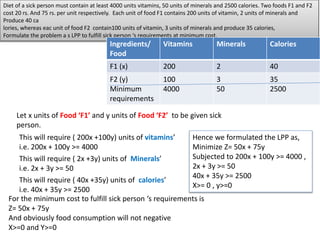
This document provides an introduction to linear programming, including: - Linear programming originated during World War 2 to optimally allocate limited resources. - It involves identifying decision variables, constraints as linear equations, non-negativity restrictions, and an objective function to maximize or minimize. - Two examples of formulating linear programming problems (LPPs) are provided: determining the optimal product mix to maximize profit for a company, and minimizing the cost of a diet to meet a sick person's nutritional requirements. - Graphical solution methods for LPPs include the iso-profit and corner point methods.

1. Linear
Programming
BY
Prof. RAHUL TRIPATHI
B.TECH(CSE)

2. Introduction
• It will be interest to known that the linear programming had its origin during the 2nd world war. (1938-
1945)
• Linear programming is the most popular mathematical techinque which is involve the limiting resource in
an optimal manner.
• The term programming means planning to minimize cost or maximize profit or minimum use of
resources or minimize the time etc.(Refer Page no. 1243 HK DASS)
• During the world war-II MARSHALL K. WOOD worked on the allocation of the resources for the UNITED
STATES. Method were developed to allocate resources in such way as to minimize the desired object of
the problem.
• George B. Dantig was a member of the air force group who devised the Simple method in 1947.

3. Working rule to formulate the LPP
There are four step in mathematical formulation of linear programming problem as a mathematical model
1)Identify the decision variable ad assign symbols x, y to them
2) Identify the set of constraints and express them as linear equation in term of decision variable.
3)Introduce non-negative restrictions.
4)Identify the objective function to be optimized(i. e. maximize or minimize and express it as linear
function.
For example:
A company manufacture two types of chemicals A and B. Each chemical requires two types of raw materials
P and Q . The table below shows number of unit of A and one unit of B and the total availability of P and
Q.
Chemicals/Raw
mater
A B Avail.
P 3 2 120
Q 2 5 160
The company gets profit of 360rs and 400rs by selling one unit of A and one unit of B respectively.
How many units of A and B should be manufacture so that the company gets maximum profit?
(Assume that the entire production of A and B are sold.). Find the problem as LPP

4. Let x units of chemical ‘A’ and y units of chemical ‘B’ is produced.
Chemical/Ra
w material
A
(x)
B
(y)
Availibilty
P 3 2 120
Q 2 5 160
This will require ( 3x + 2y) units of Raw material ‘P’
i.e. 3x + 2y <= 120
And ( 2x + 5y) units of Raw material ‘Q’
i.e. 2x + 5y <= 160
As it is assumed that entire production of ‘A’ and ‘B’ can be sold
i.e. x>= 0 and y>=0
Profit z obtained by x unit of A and y unit of B is
Z= 350x + 400y
Hence we formulated the LPP as,
Maximize z = 350x + 400y
Subjected to 3x + 2y <=120, 2x + 5y <= 160
X>= 0 , y>=0

5. Diet of a sick person must contain at least 4000 units vitamins, 50 units of minerals and 2500 calories. Two foods F1 and F2
cost 20 rs. And 75 rs. per unit respectively. Each unit of food F1 contains 200 units of vitamin, 2 units of minerals and
Produce 40 ca
lories, whereas eac unit of food F2 contain100 units of vitamin, 3 units of minerals and produce 35 calories,
Formulate the problem a s LPP to fulfill sick person ‘s requirements at minimum cost.
Ingredients/
Food
Vitamins Minerals Calories
F1 (x) 200 2 40
F2 (y)
Minimum
requirements
100
4000
3
50
35
2500
Let x units of Food ‘F1’ and y units of Food ‘F2’ to be given sick
person.
This will require ( 200x +100y) units of vitamins’
i.e. 200x + 100y >= 4000
This will require ( 2x +3y) units of Minerals’
i.e. 2x + 3y >= 50
This will require ( 40x +35y) units of calories’
i.e. 40x + 35y >= 2500
For the minimum cost to fulfill sick person ‘s requirements is
Z= 50x + 75y
And obviously food consumption will not negative
X>=0 and Y>=0
Hence we formulated the LPP as,
Minimize Z= 50x + 75y
Subjected to 200x + 100y >= 4000 ,
2x + 3y >= 50
40x + 35y >= 2500
X>= 0 , y>=0

6. No question will ask from 9.1
So don’t worry about this

7. Solution of LPP by graphical
a) Iso- profit method
b) Corner point method
Solve the following LPP using graphical method
1) Maximize z= 11x + 8y
Subject to x<=4, y<=6, x+y<= 6, x>=0, y>=0
Exercise 9.2(All problem)
Refer class note book
Thank you so much!!!
For any query
Contact Num. – 8879490537
Email- rtiwarirahul123@gmail.com