Ley de composición interna algebra ii

ÁLGEBRA
ESTUDIANTE: ACHARTE PRADO WILBER
CICLO: QUINTO
MATEMÁTICA COMPUTACIÓN E INFORMÁTICA

AL
2021- BICENTENARIO -PERU
SOLUCIÓN DE LOS PROBLEMAS
2021-UNH

AL
PRÁCTICA CALIFICADA N° 01 LEY DE COMPOSICIÓN INTERNA
1. Estudiar sus propiedades de la ley de composición interna, mediante las siguientes
operaciones en ⋇:
a. a⋇b = ab + 1; ∀a,b ∈ℤ
SOLUCION:
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION:
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(ab + 1)*c=a*( bc + 1)………por definición
(ab + 1).c+1=a.(bc+1) +1……por definición
abc + c + 1 ≠ abc + a + 1…por distributiva multiplicativa con respecto a la adición
• * NO ES ASOCIATIVO EN Z
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝐷𝐸𝑀𝑂𝑆𝑇𝑅𝐴𝐶𝐼𝑂𝑁
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎𝑏 + 1 = 𝑏𝑎 +1 …………por definición
* ES CONMUTATIVO EN Z
ELEMENTO NEUTRO
∀𝑎𝜖𝑍∃! 𝑒 ∈ 𝑍/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝐷𝐸𝑀𝑂𝑆𝑇𝑅𝐴𝐶𝐼𝑂𝑁:
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 𝑒 ∗ 𝑎 = 𝑎
Por definición
ae+1=a ea+1=ae+1 ea+1=a
ae=a-1 0=0 e=a-1/a
e=
𝑎−1
𝑎
*NO TIENE UN ELEMENTO NEUTRO EN Z

AL
ELEMENTO SIMETRICO
∀𝑎𝜖𝑍∃! 𝑎′
∈ 𝑍/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
b. a⋇b = a + b – 1; ∀a,b ∈ℤ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏 − 1) ∗ 𝑐 = 𝑎 ∗ (𝑏 + 𝑐 − 1) … … … … 𝑝𝑜𝑟 𝑑𝑒𝑓𝑖𝑛𝑖𝑐𝑖𝑜𝑛
(𝑎 + 𝑏 − 1) + 𝑐 − 1 = 𝑎 + (𝑏 + 𝑐 − 1) − 1 … … … … … … … . 𝑝𝑜𝑟 𝑑𝑒𝑓𝑖𝑛𝑖𝑐𝑖𝑜𝑛
𝑎 + 𝑏 + 𝑐 − 2 = 𝑎 + 𝑏 + 𝑐 − 2
* ES ASCIATIVO EN Z
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 + 𝑏 − 1 = 𝑏 + 𝑎 − 1 ……………por definición
∗ 𝐸𝑆 𝐶𝑂𝑁𝑀𝑈𝑇𝐴𝑇𝐼𝑉𝑂 𝐸𝑁 𝑍
ELEMENTO NEUTRO
∀𝑎𝜖𝑍∃! 𝑒 ∈ 𝑍/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 + 𝑒 − 1 = 𝑎 𝑒 + 𝑎 − 1 = 𝑎 𝑎 + 𝑒 − 1 = 𝑒 + 𝑎 − 1
𝑒 = 1 𝑒 = 1 =
𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑁𝐷𝑂 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑁𝐷𝑂 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑁𝐷𝑂
𝑎 + 1 − 1 = 𝑎 1 + 𝑎 − 1 = 𝑎 𝑎 + 1 − 1 = 1 + 𝑎 − 1
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎
* TIENE UN ELEMENTO NEUTRO EN Z

AL
ELEMENTO SIMETRICO
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
𝑎 + 𝑎′
− 1 = 1 𝑎′
+ 𝑎 − 1 = 1 𝑎 + 𝑎′
− 1 = 𝑎′
+ 𝑎 − 1
𝑎´ = 2 − 𝑎 𝑎′
= 2 − 𝑎
Reemplazando 𝑟𝑒𝑒𝑚𝑝𝑙𝑎𝑧𝑎𝑛𝑑𝑜 𝑅𝑒𝑒𝑚𝑝𝑙𝑎𝑧𝑎𝑛𝑑𝑜
𝑎 + (2 − 𝑎) − 1 = 1 2 − 𝑎 + 𝑎 − 1 = 1 𝑎 + 2 − 𝑎 − 1 = 2 − 𝑎 + 𝑎 − 1
1 = 1 1 = 1 1 = 1
• * TIENE UN SIMETRICO EN Z
c. a⋇b = (ab) / 2; ∀a,b ∈ℚ+
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑄+
/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
𝑎𝑏
2
∗ 𝑐 = 𝑎 ∗
𝑏𝑐
2
…………..por definición.
𝑎𝑏
2
.𝑐
2
=
𝑏𝑐
2
.𝑎
2
……………….por definición.
𝑎𝑏𝑐
4
=
𝑏𝑐𝑎
4
ES ASOCIATIVO EN 𝑄+
ELEMENTO NEUTRO
∀𝑎𝜖𝑍∃! 𝑒 ∈ 𝑄+
/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 𝑒 ∗ 𝑎 = 𝑎
𝑎𝑒
2
= 𝑎
𝑒𝑎
2
=
𝑎𝑒
2
𝑒𝑎
2
= 𝑎
𝑒 =
2𝑎
𝑎
𝑒 =
2𝑎
𝑎
𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑁𝐷𝑂 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑁𝐷𝑂 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑀𝑂𝑆
𝑎(
2𝑎
𝑎
)
2
= 𝑎
(
2𝑎
𝑎
)𝑎
2
=
𝑎(
2𝑎
𝑎
)
2
(
2𝑎
𝑎
𝑎
2
= 𝑎
2𝑎
2
= 𝑎
2𝑎
2
=
2𝑎
2
2𝑎
2
= 𝑎
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎
* TIENE NEUTRO EN 𝑄+
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑄+
/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎𝑏
2
=
𝑏𝑎
2
* ES CONMUTATIVO EN 𝑄+

AL
ELEMENTO SIMETRICO
DEMOSTRACION
∀𝑎𝜖𝑄+
∃! 𝑎′
∈ 𝑄+
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
𝑎𝑎′
2
=
2𝑎
𝑎
𝑎′𝑎
2
=
2𝑎
𝑎
𝑎.𝑎′
2
=
𝑎′.𝑎
2
𝑎𝑎′
=
2𝑎
𝑎
. 2 𝑎′
𝑎 =
2𝑎
𝑎
. 2 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑀𝑂𝑆
𝑎′ =
2𝑎
𝑎
.2
𝑎
𝑎′
=
2𝑎
𝑎
𝑎
.2
𝑎.(
4
𝑎
)
2
=
(
4
𝑎
).𝑎
2
𝑎′
=
4𝑎
𝑎
𝑎
=
4
𝑎
𝑎′
=
4
𝑎
4
2
=
4
2
𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑀𝑂𝑆 𝑅𝐸𝐸𝑀𝑃𝐿𝐴𝑍𝐴𝑀𝑂𝑆 2 = 2
𝑎(
4
𝑎
)
2
=
2𝑎
𝑎
=
4
2
= 2
(
4
𝑎
)𝑎
2
=
2𝑎
𝑎
=
4
2
= 2
2 = 2 2 = 2
* ES SIMETRICO EN 𝑄+
d. a⋇b = (ab) / (a+b); ∀a,b ∈ℝ+
ASOCIATIVA
DEMOSTRACION
∀𝑎, 𝑏, 𝑐𝜖𝑅+
/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎𝑏)
𝑎+𝑏
∗ 𝐶 = 𝑎 ∗
(𝑏𝑐)
𝑏+𝑐
…………………… por definición
(𝑎𝑏)
𝑎+𝑏
.𝐶
(𝑎𝑏)
𝑎+𝑏
+𝐶
=
𝑎.
(𝑏𝑐)
𝑏+𝑐
𝑎+
(𝑏𝑐)
𝑏+𝑐
…………………………… por definición
𝑎𝑏𝑐
𝑎+𝑏
(𝑎𝑏)+(𝑎+𝑏)𝑐
𝑎+𝑏
=
𝑎𝑏𝑐
𝑏+𝑐
𝑎(𝑏+𝑐)+(𝑏𝑐)
𝑏+𝑐
𝑎𝑏𝑐
𝑎+𝑏
(𝑎𝑏)+(𝑎𝑐+𝑏𝑐)
𝑎+𝑏
=
𝑎𝑏𝑐
𝑏+𝑐
(𝑎𝑏+𝑎𝑐)+(𝑏𝑐)
𝑏+𝑐
𝑎2𝑏𝑐+𝑎𝑏2𝑐
𝑎2𝑏+𝑎2𝑐+2(𝑎𝑏𝑐)+𝑎𝑏2+𝑏2𝑐
≠
𝑎2𝑏𝑐+𝑎𝑏2𝑐
𝑎𝑏2+2(𝑎𝑏𝑐)+𝑏2𝑐+𝑎𝑐2+𝑏𝑐2
* NO ES ASOCIATIVO EN 𝑅+

AL
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅+
/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
(𝑎𝑏)
𝑎+𝑏
=
(𝑏𝑎)
𝑏+𝑎
* ES CONMUTATIVO EN 𝑅+
ELEMENTO NEUTRO
∀𝑎𝜖𝑅+
∃! 𝑒 ∈ 𝑅+
/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 𝑒 ∗ 𝑎 = 𝑎
(𝑎𝑒)
𝑎+𝑒
= 𝑎
(𝑒𝑎)
𝑒+𝑎
=
(𝑎𝑒)
𝑎+𝑒
(𝑒𝑎)
𝑒+𝑎
= 𝑎
𝑎𝑒 = 𝑎(𝑎 + 𝑒) 𝑒𝑎 = 𝑎(𝑒 + 𝑎)
𝑎𝑒 = 𝑎2
+ 𝑎𝑒 𝑒𝑎 = 𝑎𝑒 + 𝑎2
𝑒 =
𝑎2+𝑎𝑒
𝑎
𝑒 =
𝑎𝑒+𝑎2
𝑎
𝑒 = 𝑎 + 𝑒 𝑒 = 𝑒 + 𝑎
0 = 𝑎…no es cierto 0 = 𝑎 … 𝑛𝑜 𝑒𝑠 𝑐𝑖𝑒𝑟𝑡𝑜
* NO TIENE ELEMENTO NEUTRO EN 𝑅+
ELEMENTO SIMETRICO
∀𝑎𝜖𝑅+
∃! 𝑎′
∈ 𝑅+
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
• * TAMPOCO TIENE SIMETRIA EN 𝑅+
e. a ⋇ b = a + ba2; ∀a,b ∈ℝ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑅 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏𝑎2) ∗ 𝑐 = 𝑎 ∗ (𝑎 + 𝑏𝑎2) ………………………por definición.
(𝑎 + 𝑏𝑎2) + (𝑐(𝑎 + 𝑏𝑎2)2
) = 𝑎 + ((𝑎 + 𝑏𝑎2)𝑎2
) ………por definición
(𝑎 + 𝑏𝑎2) + (𝑐(𝑎2
+ 2(𝑎)(𝑏𝑎2) + ( 𝑏𝑎2
)2
) ≠ 𝑎 + 𝑎3
+ 𝑏𝑎4
∗ 𝑁𝑂 𝐸𝑆 𝐴𝑆𝑂𝐶𝐼𝐴𝑇𝐼𝑉𝑂 𝐸𝑁 𝑅

AL
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
(𝑎 + 𝑏𝑎2) ≠ (𝑏 + 𝑎𝑏2) ………
• * NO ES CONMUTATIVO EN R
ELEMENTO NEUTRO
∀𝑎𝜖𝑅∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 𝑒 ∗ 𝑎 = 𝑎
(𝑎 + 𝑒𝑎2) = 𝑎
𝑒 2
= 𝑎 − 𝑎
𝑒𝑎2
= 0 …
∗ 𝑁𝑂 𝐸𝑆 𝑁𝐸𝑈𝑇𝑅𝑂 𝐸𝑁 𝑅
ELEMENTO SIMETRICO
∀𝑎𝜖𝑅∃! 𝑎′
∈ 𝑅/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
• TAMPOCO ES SIMETRICO EN R
f. a⋇b = a + b – 3; ∀a,b ∈ℝ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑅 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏 − 3) ∗ 𝑐 = 𝑎 ∗ (𝑏 + 𝑐 − 3) … … … … ………por definición
(𝑎 + 𝑏 − 3) + 𝑐 − 3 = 𝑎 + (𝑏 + 𝑐 − 3) − 3 ……….por definición
𝑎 + 𝑏 + 𝑐 − 6 = 𝑎 + 𝑏 + 𝑐 − 6
✓ ES ASOCIATIVO EN R.
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
(𝑎 + 𝑏 − 3) = (𝑏 + 𝑎 − 3)
✓ ES CONMUTATIVO EN R

AL
ELEMENTO NEUTRO
∀𝑎𝜖𝑅∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
DEMOSTRACION
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 + 𝑒 − 3 = 𝑎 𝑒 + 𝑎 − 3 = 𝑎 𝑎 + 𝑒 − 3 = 𝑒 + 𝑎 − 3
𝑒 = 3 𝑒 = 3
Reemplazando Reemplazando Reemplazando
𝑎 + 3 − 3 = 𝑎 3 + 𝑎 − 3 = 𝑎 𝑎 + 3 − 3 = 3 + 𝑎 − 3
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎
ELEMENTO SIMETRICO
∈ 𝑅/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑑𝑒𝑚𝑜𝑠𝑡𝑟𝑎𝑐𝑖𝑜𝑛
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
𝑎 + 𝑎′
− 3 = 3 𝑎′ + 𝑎 − 3 = 3 𝑎 + 𝑎′
− 3 = 𝑎′ + 𝑎 − 3
𝑎′
= 6 − 𝑎 𝑎′
= 6 − 𝑎
𝑎 + (6 − 𝑎) − 3 = 3 6 − 𝑎 + 𝑎 − 3 = 3 3 𝑎 + 6 − 𝑎 − 3 = 6 − 𝑎 + 𝑎 − 3
3 = 3 3 = 3 3 = 3
g. a⋇b = ab + 2; ∀a,b ∈ℝ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑅 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
Demostración
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎𝑏 + 2) ∗ 𝑐 = 𝑎 ∗ (𝑏𝑐 + 2) ……por definición
(𝑎𝑏 + 2). 𝑐 + 2 = 𝑎. (𝑏𝑐 + 2) + 2 ……por definición
𝑎𝑏𝑐 + 2𝑐 + 2 ≠ 𝑎𝑏𝑐 + 2𝑎 + 2…………por distributiva multiplicativa con respeto a la adición
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝐷𝐸𝑀𝑂𝑆𝑅𝐴𝐶𝐼𝑂𝑁
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎𝑏 + 2 = 𝑏𝑎 + 2

AL
ELEMENTO NEUTRO
∀𝑎𝜖𝑅∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
DEMOSTRACION
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎𝑒 + 2 = 𝑎 𝑒𝑎 + 2 = 𝑎 𝑎𝑒 + 2 = 𝑒𝑎 + 2
𝑒 = −1 𝑒 = −1
Reemplazando
𝑎𝑒 + 2 = 𝑎
𝑎(−1) + 2 = 𝑎
−𝑎 + 2 = 𝑎
2 = 𝑎 + 𝑎
2 ≠ 2𝑎 ………por lo tanto esta propiedad no cumple la ley de composición interna en R
ELEMENTO SIMETRICO
∈ 𝑅/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
Demostración
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = −1 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
𝑎𝑎′
+ 2 = −1 𝑎𝑎′
+ 2 = −1 𝑎𝑎′
+ 2 = 𝑎′
𝑎 + 2
𝑎𝑎′
= −1 − 2 𝑎′
= −
3
𝑎
𝑎′
=
−3
𝑎
Reemplazando a’=
−3
𝑎
reemplazando a’=
−3
𝑎
reemplazando a’=
−3
𝑎
𝑎𝑎′
+ 2 = −1 𝑎𝑎′
+ 2 = −1 𝑎𝑎′
+ 2 = 𝑎′
𝑎 + 2
𝑎(
−3
𝑎
) + 2 = −1 𝑎(−
3
𝑎
) + 2 = −1 𝑎 (−
3
𝑎
) + 2 = (−
3
𝑎
) 𝑎 + 2
−3𝑎
𝑎
= −3 −3 = −3 −3 + 2 = −3 + 2
−3 = −3 −1 = −1

AL
h. a⋇b = a + b + 3; ∀a,b ∈ℝ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑅 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏 + 3) ∗ 𝑐 = 𝑎 ∗ (𝑏 + 𝑐 + 3)
(𝑎 + 𝑏 + 3) + 𝑐 + 3 = 𝑎 + (𝑏 + 𝑐 + 3) + 3
𝑎 + 𝑏 + 𝑐 + 6 = 𝑎 + 𝑏 + 𝑐 + 6
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 + 𝑏 + 3 = 𝑏 + 𝑎 + 3
ELEMENTO NEUTRO
∀𝑎𝜖𝑅∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 + 𝑒 + 3 = 𝑎 𝑒 + 𝑎 + 3 = 𝑎 𝑎 + 𝑒 + 3 = 𝑒 + 𝑎 + 3
𝑒 = −3 𝑒 = −3
REEMPLAZANDO REEMPLAZANDO REEMPLAZANDO
𝑎 + 𝑒 + 3 = 𝑎 𝑒 + 𝑎 + 3 = 𝑎 𝑎 + 𝑒 + 3 = 𝑒 + 𝑎 + 3
𝑎 + (−3) + 3 = 𝑎 (−3) + 𝑎 + 3 = 𝑎 𝑎 + (−3) + 3 = (−3) + 𝑎 + 3
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎

AL
ELEMENTO SIMETRICO
∈ 𝑅/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
𝑎 + 𝑎′
+ 3 = −3 𝑎′ + 𝑎 + 3 = −3 𝑎 + 𝑎′
+ 3 = 𝑎′ + 𝑎 + 3
𝑎′
= −6 − 𝑎 𝑎′
= −6 − 𝑎
𝑎′
= −6 − 𝑎
𝑎 + 𝑎′
+ 3 = −3 𝑎′ + 𝑎 + 3 = −3 𝑎 + 𝑎′
+ 3 = 𝑎′ + 𝑎 + 3
𝑎 + (−6 − 𝑎) + 3 = −3 −6 − 𝑎 + 𝑎 + 3 = −3 𝑎 + (−6 − 𝑎) + 3 = −6 − 𝑎 + 𝑎 + 3
𝑎 − 6 − 𝑎 + 3 = −3 −3 = −3 −3 = −3
−3 = −3
∃𝒂′
∈ 𝑹/ 𝒂′
= −𝟔 − 𝒂; ∀𝒂 ∈ 𝑹
i. a⋇b = a/b; ∀a,b ∈ℚ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑄/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
𝑎
𝑏
∗ 𝑐 = 𝑎 ∗
𝑏
𝑐
𝑎
𝑏
𝑐
=
𝑎
𝑏
𝑐
𝑎
𝑏𝑐
≠
𝑎𝑐
𝑏
NO CUMPLE CON LA LEY DE COMPOSICION INTERNA EN LOS RACIONALES
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑄/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
DEMOSTRACION
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎
𝑏
≠
𝑏
𝑎
……..NO CUMPLE LA LEY DE COMPOSICION INTERNA EN Q

AL
ELEMENTO NEUTRO
∀𝑎𝜖𝑄∃! 𝑒 ∈ 𝑄/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎
𝑒
= 𝑎
𝑒
𝑎
= 𝑎
𝑎 = 𝑎𝑒 𝑒 = 𝑎𝑎
𝑎
𝑎
= 𝑒 𝑒 = 𝑎2
1 = 𝑒
NO CUMPLE CON LA LEY DE COMPOSICION INTERNA EN Q
ELEMENTO SIMETRICO
∀𝑎𝜖𝑄∃! 𝑎′
∈ 𝑄/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
No cumple
j. a⋇b = a/b; ∀a,b ∈ℤ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
𝑎
𝑏
∗ 𝑐 = 𝑎 ∗
𝑏
𝑐
𝑎
𝑏
𝑐
=
𝑎
𝑏
𝑐
𝑎
𝑏𝑐
≠
𝑎𝑐
𝑏
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎
𝑏
≠
𝑏
𝑎
…………NO CUMPLE LA LCI EN Z.

AL
ELEMENTO NEUTRO
∀𝑎𝜖𝑍, ∃! 𝑒 ∈ 𝑍/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
DEMOSTRACION
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎
𝑒
= 𝑎
𝑒
𝑎
= 𝑎
𝑎
𝑒
=
𝑒
𝑎
𝑎 = 𝑎𝑒 𝑒 = 𝑎2
𝑎
𝑎
= 𝑒
1 = 𝑒
NO CUMPLE LA LEY DE COMPOSICIÓN INTERNA EN Z
ELEMENTO SIMETRICO
∈ 𝑍/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
NO CUMPLE LA LEY DE COMPOSICION INTERNA.
k. a⋇b = a – b; ∀a,b ∈ℤ+
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑍+
/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 − 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 − 𝑐)
(𝑎 − 𝑏) − 𝑐 = 𝑎 − (𝑏 − 𝑐)
𝑎 + 𝑏 − 𝑐 ≠ 𝑎 − 𝑏 + 𝑐
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑍+
/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 − 𝑏 ≠ 𝑏 − 𝑎
NO CUMPLE CON LA LEY DE COMPOSICION INTERNA
ELEMENTO NEUTRO
∀𝑎𝜖𝑍+
∃! 𝑒 ∈ 𝑍+
/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 − 𝑒 = 𝑎
−𝑒 = 𝑎 − 𝑎
−𝑒 = 0
𝑒 = −0.......NO CUMPLE LA LEY DE COMPOSICION INTERNA EN 𝑍+

AL
ELEMENTO SIMETRICO
∀𝑎𝜖𝑍+
∃! 𝑎′
∈ 𝑍+
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐼𝑅𝐼𝐴 𝐿𝐴 𝐿𝐸𝑌 𝐷𝐸 𝐶𝑂𝑀𝑃𝑂𝑆𝐼𝐶𝐼𝑂𝑁 𝐼𝑁𝑇𝐸𝑅𝑁𝐴 𝐸𝑁 𝑍+
l. a⋇b = ab ; ∀a,b ∈ℤ+
ASOCIATIVA
/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
𝑎𝑏
∗ 𝑐 = 𝑎 ∗ 𝑏𝑐
(𝑎𝑏
)𝑐
≠ (𝑎)𝑏𝑐
𝑁𝑂 𝑆𝐸 𝐶𝑈𝑀𝑃𝐿𝐸 𝐿𝐴 𝐴𝑆𝑂𝐶𝐼𝐴𝑇𝐼𝑉𝐼𝐷𝐴𝐷 𝐸𝑁 𝑍+
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎𝑏
≠ 𝑏𝑎
𝑁𝑂 𝑆𝐸 𝐶𝑈𝑀𝑃𝐿𝐼𝑅𝐼𝐴 𝐿𝐴 𝐶𝑂𝑁𝑀𝑈𝑇𝐴𝑇𝐼𝑉𝐼𝐷𝐴𝐷 𝐸𝑁 𝑍+
ELEMENTO NEUTRO
∀𝑎𝜖𝑍+
∃! 𝑒 ∈ 𝑍+
/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎𝑒
= 𝑎 𝑒𝑎
= 𝑎
𝑑𝑒 𝑎𝑐𝑢𝑒𝑟𝑑𝑜 𝑎 𝑙𝑎 𝑝𝑟𝑜𝑝𝑖𝑒𝑑𝑎𝑑 𝑑𝑒 𝑙𝑜𝑠
𝑒𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑒𝑠 e𝑛𝑒𝑐𝑒𝑠𝑎𝑟𝑖𝑎𝑚𝑒𝑛𝑡𝑒𝑡𝑒𝑛𝑑𝑟𝑖𝑎 𝑞𝑢𝑒 𝑠𝑒𝑟 𝑢𝑛𝑜
𝑒 = 1
POR LO TANTO NO ESTA PROPIEDAD NO CUMPLE LA( LCI) EN 𝑍+
ELEMENTO SIMETRICO
∀𝑎𝜖𝑍+
∃! 𝑎′
∈ 𝑍+
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
TAMPOCO CUMPLIRIA LA LCI YA QUE NO ENCONTRAMOS UN ELEMENTO NEUTRO
“e”

AL
m. a⋇b = a – b; ∀a,b ∈ℝ
ASOCIATIVA
∀𝑎, 𝑏, 𝑐𝜖𝑅 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 − 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 − 𝑐)
(𝑎 − 𝑏) − 𝑐 ≠ 𝑎 − (𝑏 − 𝑐) ..
𝑁𝑂 𝑆𝐸 𝐶𝑈𝑀𝑃𝐿𝐸 (𝐿𝐶𝐼) 𝐸𝑁 𝐿𝐴 𝑆𝑂𝐶𝐼𝑇𝐼𝑉𝐴 𝐸𝑁 (𝑅)
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑅/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
DEMOSTRACION
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 − 𝑏 = 𝑏 − 𝑎
ELEMENTO NEUTRO
∀𝑎𝜖𝑅∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 − 𝑒 = 𝑎 𝑒 − 𝑎 = 𝑎
−𝑒 = 𝑎 − 𝑎 𝑒 = 𝑎 + 𝑎
𝑒 = −0 𝑒 = 2𝑎
ELEMENTO SIMETRICO
∈ 𝑅/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
TAMPOCO CUMPLIRIA PUESTO QUE NO SE HA ENCONTRADO UN ELEMENTO
NUTRO
n. En (ℤ+,⋇) se define a⋇b = c, donde c es el menor entero mayor que la suma de a y b.
Podemos apreciar lo siguiente:
𝑍+
𝑥 𝑍+
→ 𝑍+
𝑎 + 𝑏 ≤ 𝑎 ∗ 𝑏 = 𝑐
𝑐 > 𝑎 + 𝑏
Calculamos por el método de tanteo, para comprobar si es cierto.
𝑎 = 4 𝑐 > 4 + 5
𝑏 = 5 𝑐 > 9
El menor entero, mayor que la suma de a y b será: 10.
Entonces diremos que ∗ cumple LCI en 𝑍+

AL
o. En (ℤ+,⋇) se define a⋇b = c, donde c es el mayor entero menor que el producto de a y
b.
SOLUCION
𝑍+
𝑥 𝑍+
→ 𝑍+
𝐶 = 𝑎 ∗ 𝑏 > 𝑎. 𝑏
𝐶 < 𝑎. 𝑏
Calculamos esto, por el método del tanteo.
𝑎 = 2 𝐶 < 2.5
𝑎 = 5 𝐶 < 10
Entonces el mayor entero, menor que el producto e a y b es 9.
Por lo tanto ∗ cumple LCI en 𝑍+
p. En (ℤ+,⋇) se define a⋇b=c, donde c es al menos 5 unidades mayor que a+b
𝑍+
𝑥 𝑍+
→ 𝑍+
𝑎 ⋇ 𝑏 = 𝑐
𝑐 + 5 > 𝑎 + 𝑏
Calculamos por el método del tanteo
𝑎 = 7 𝑐 + 5 > 7 + 6
𝑎 = 6 𝑐 > 13
Entonces el numero c que al menos es cinco unidades mayores que a + b seria
18.
q. S es un conjunto de todas las funciones con valores reales en (ℝ, ⋇), definido por f⋇g
= h, donde h(x) = f(x) + g(x).
𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑓(𝑥) + 𝑔(𝑥) ……definición.
𝐴𝑆𝑂𝐶𝐼𝐴𝑇𝐼𝑉𝐴
∀𝑓(𝑥), 𝑔(𝑥), 𝑚(𝑥) ∈ 𝑅 / (𝑓(𝑥) ∗ 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥)) ∗ 𝑚(𝑥))
DEMOSTRACION
(𝑓(𝑥) ∗ 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥)) ∗ 𝑚(𝑥))
(𝑓(𝑥) + 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥) + 𝑚(𝑥))
(𝑓(𝑥) + 𝑔(𝑥)) + 𝑚(𝑥) = 𝑓(𝑥) + (𝑔(𝑥) + 𝑚(𝑥))
∗ 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑣𝑜 𝑒𝑛 𝑅

AL
𝐶𝑂𝑁𝑀𝑈𝑇𝐴𝑇𝐼𝑉𝐴
∀𝑓(𝑥), 𝑔(𝑥) ∈ 𝑅/ 𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑔(𝑥) ∗ 𝑓(𝑥)
DEMOSTRACION
𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑔(𝑥) ∗ 𝑓(𝑥)
𝑓(𝑥) + 𝑔(𝑥) = 𝑔(𝑥) + 𝑓(𝑥)
∗ 𝑒𝑠 𝑐𝑜𝑛𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑜 𝑒𝑛 𝑅
𝐸𝐿𝐸𝑀𝐸𝑁𝑇𝑂 𝑁𝐸𝑈𝑇𝑅𝑂
∀𝑓(𝑥) ∈ 𝑅, ∃! 𝑒 ∈ 𝑅/ 𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑒(𝑥) ∗ 𝑓(𝑥) = 𝑓(𝑥)
DEMOSTRACION
1. REEMPLAZANDO
𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑓(𝑥) 𝑓(𝑥) + 0 = 𝑓(𝑥)
𝑓(𝑥) + 𝑒(𝑥) = 𝑓(𝑥) 𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) = 𝑓(𝑥) − 𝑓(𝑥)
𝑒(𝑥) = 0
Necesariamente 𝑒(𝑥) ≠ 0
2.
𝑒(𝑥) ∗ 𝑓(𝑥) = 𝑓(𝑥) 0 + 𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) + 𝑓(𝑥) = 𝑓(𝑥) 𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) = 0
3.
𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑒(𝑥) ∗ 𝑓(𝑥)
𝑓(𝑥) + 0 = 0 + 𝑓(𝑥)
𝑓(𝑥) = 𝑓(𝑥)
∗ 𝑛𝑜 𝑡𝑖𝑒𝑛𝑒 𝑒𝑙𝑚𝑒𝑛𝑡𝑜 𝑛𝑒𝑢𝑡𝑟𝑜 𝑒𝑛 𝑅
𝑬𝑳𝑬𝑴𝑬𝑵𝑻𝑶 𝑺𝑰𝑴𝑬𝑻𝑹𝑰𝑪𝑶
∗ 𝑁𝑜 𝑡𝑖𝑒𝑛𝑒 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝑠𝑖𝑚𝑒𝑡𝑟𝑖𝑐𝑜, 𝑝𝑢𝑒𝑠𝑡𝑜 𝑞𝑢𝑒 𝑛𝑜 𝑐𝑢𝑚𝑝𝑙𝑒 𝑐𝑜𝑛 𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝑛𝑒𝑢𝑡𝑟𝑜.

AL
r. S un conjunto de todas las funciones con valores reales en (ℝ, ⋇) definida por f ⋇ g =
h; h(x)= f(x). g(x)
𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑓(𝑥) . 𝑔(𝑥) ……definición.
ASOCIATIVA
∀𝑓(𝑥), 𝑔(𝑥), 𝑚(𝑥) ∈ 𝑅 / (𝑓(𝑥) ∗ 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥)) ∗ 𝑚(𝑥))
DEMOSTRACION
(𝑓(𝑥) ∗ 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥)) ∗ 𝑚(𝑥))
(𝑓(𝑥) . 𝑔(𝑥)) ∗ 𝑚(𝑥) = 𝑓(𝑥) ∗ (𝑔(𝑥) . 𝑚(𝑥))
𝑓(𝑥). 𝑔(𝑥). 𝑚(𝑥) = 𝑓(𝑥) . 𝑔(𝑥) . 𝑚(𝑥)
CONMUTATIVA
∀𝑓(𝑥), 𝑔(𝑥) ∈ 𝑅/ 𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑔(𝑥) ∗ 𝑓(𝑥)
DEMOSTRACION
𝑓(𝑥) ∗ 𝑔(𝑥) = 𝑔(𝑥) ∗ 𝑓(𝑥)
𝑓(𝑥) . 𝑔(𝑥) = 𝑔(𝑥) . 𝑓(𝑥)
ELEMENTO NEUTRO
∀𝑓(𝑥) ∈ 𝑅, ∃! 𝑒 ∈ 𝑅/ 𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑒(𝑥) ∗ 𝑓(𝑥) = 𝑓(𝑥)
DEMOSTRACION
1. REEMPLAZANDO
𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑓(𝑥) 𝑓(𝑥) . 𝑒(𝑥) = 𝑓(𝑥)
𝑓(𝑥) . 𝑒(𝑥) = 𝑓(𝑥) 𝑓(𝑥) . 1 = 𝑓(𝑥)
𝑒(𝑥) =
𝑓(𝑥)
𝑓(𝑥)
𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) = 1
2. REEMPLAZANDO
𝑒(𝑥) ∗ 𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) . 𝑓(𝑥) = 𝑓(𝑥) 1 . 𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) =
𝑓(𝑥)
𝑓(𝑥)
𝑓(𝑥) = 𝑓(𝑥)
𝑒(𝑥) = 1
3.
𝑓(𝑥) ∗ 𝑒(𝑥) = 𝑒(𝑥) ∗ 𝑓(𝑥)
𝑓(𝑥) . 𝑒(𝑥) = 𝑒(𝑥) . 𝑓(𝑥)
𝑓(𝑥) . 1 = 1 . 𝑓(𝑥)
𝑓(𝑥) = 𝑓(𝑥)

AL
ELEMENTO SIMETRICO
∀𝑓(𝑥) ∈ 𝑅, ∃! 𝑓(𝑥)′
/ 𝑓(𝑥) ∗ 𝑓(𝑥)′ = 𝑓(𝑥)′ ∗ 𝑓(𝑥) = 𝑒(𝑥)
DEMOSTRACION
1. REEMPLAZANDO
𝑓(𝑥) ∗ 𝑓(𝑥)′
= 𝑒(𝑥) 𝑓(𝑥) . 𝑓(𝑥)′
= 1
𝑓(𝑥) . 𝑓(𝑥)′
= 1 𝑓(𝑥) .
1
𝑓(𝑥)
= 1
𝑓(𝑥)′
=
1
𝑓(𝑥)
con 𝑓(𝑥) ≠ 0 1 = 1
2.
𝑓(𝑥)′ ∗ 𝑓(𝑥) = 𝑒(𝑥) REEMPLAZANDO
𝑓(𝑥)′
. 𝑓(𝑥) = 1
1
𝑓(𝑥)
. 𝑓(𝑥) = 1
𝑓(𝑥)′
=
1
𝑓(𝑥)
con 𝑓(𝑥) ≠ 0 1 = 1
3.
𝑓(𝑥) ∗ 𝑓(𝑥)′ = 𝑓(𝑥)′ ∗ 𝑓(𝑥)
𝑓(𝑥) .
1
𝑓(𝑥)
=
1
𝑓(𝑥)
. 𝑓(𝑥)
1 = 1
s. Sea S un conjunto formado por 10 personas, todas ellas con diferente estatura,
definida por a ⋇ b = c, donde c es la persona más alta de las 10 en S.
1p.
2p.
3p.
4p.
5p.
6p.
7p.
8p.
9p.
10p.
S
1p. =talla 1
2p.=talla 2
3p.=talla 3
4p.=talla 4
5p.=talla 5
6p.=talla 6
7p.=talla7
8p.=talla 8
9p.=talla 9
10p=talla 10

AL
2. Para toda operación binaria ⋇ definida a continuación, determínese cuál ⋇ es conmutativa y
cuál asociativo.
a. En ℤ, defínase ⋇ por a⋇b = a – b
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 − 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 − 𝑐)
(𝑎 − 𝑏) − 𝑐 ≠ 𝑎 − (𝑏 − 𝑐)
CONMUTATIVO
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 − 𝑏 ≠ 𝑏 − 𝑎
b. En ℚ, defínase ⋇ por a ⋇ b = ab + 1
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑄/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎𝑏 + 1) ∗ 𝑐 = 𝑎 ∗ (𝑏𝑐 + 1)
(𝑎𝑏 + 1). 𝑐 + 1 = 𝑎. (𝑏𝑐 + 1) + 1
𝑎𝑏𝑐 + 𝑐 + 1 = 𝑎𝑏𝑐 + 𝑎 + 1
CONMUTATIVO
∀𝑎, 𝑏 ∈ 𝑍/𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎𝑏 + 1 = 𝑏𝑎 + 1
c. En ℤ+, defínase ⋇ por a⋇b = 2 ab
ASOCIATIVO
/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
2𝑎𝑏
∗ 𝑐 = 𝑎 ∗ 2𝑏𝑐
2(2𝑎𝑏)𝑐
≠ 2𝑎(2𝑏𝑐)
SE CUMPLE LA
CONMUTATIVIDAD EN
ESTE OPERADOR

AL
CONMUTATIVO
∀𝑎, 𝑏 ∈ 𝑍/𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
2𝑎𝑏
= 2𝑏𝑎
d. En ℚ, defínase ⋇ por a⋇b = a + b – 1
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑄/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏 − 1) ∗ 𝑐 = 𝑎 ∗ (𝑏 + 𝑐 − 1)
(𝑎 + 𝑏 − 1) + 𝑐 − 1 = 𝑎 + (𝑏 + 𝑐 − 1) − 1
𝑎 + 𝑏 + 𝑐 − 2 = 𝑎 + 𝑏 + 𝑐 − 2
CONMUTATIVO
∀𝑎, 𝑏 ∈ 𝑄/𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 + 𝑏 − 1 = 𝑏 + 𝑎 − 1
3. ¿Falso o verdadero?
a. Si ⋇ es cualquier operación interna en cualquier conjunto S, entonces a⋇a = a; ∀a ∈S.
FALSO
b. Si ⋇ es cualquier operación interna conmutativa en cualquier conjunto S, entonces a⋇(b⋇c)
= (b⋇c) ⋇ a; ∀a,b,c ∈S
VERDADERO
c. Las únicas operaciones binarias importantes son aquellas definidas en conjuntos
numéricos.
VERDADERO
d. Una operación binaria ⋇ en un conjunto S es conmutativa si existe a,b ∈S, tal que a⋇b =
b⋇a
VERDABERO
e. Toda operación binaria definida en un conjunto de un solo elemento es conmutativo y
asociativo.
FALSO
• Se define, asociativa y
conmutativa en * por a*b=a+b-1

AL
f. Una operación binaria en un conjunto S asigna al menos un elemento de S a todo par
ordenado de elementos de S.
VERDADERO
g. Una operación binaria en un conjunto S asigna a lo más un elemento de S a todo par
VERDADERO
h. Una operación binaria en un conjunto S asigna exactamente un elemento de S a todo par
VERDADERO
i. Una operación binaria en un conjunto S puede asignar más de un elemento de S a algún
par ordenado de elementos de S.
FALSO
4. En ℤ, se define ⋇ por medio de a⋇b = 2(a+b). Estudiar sus propiedades.
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
2(𝑎 + 𝑏) ∗ 𝑐 = 𝑎 ∗ 2(𝑏 + 𝑐)
2 ((2(𝑎 + 𝑏)) + 𝑐) = 2(𝑎 + (2(𝑏 + 𝑐)
2(2𝑎 + 2𝑏 + 𝑐) = 2(𝑎 + 2𝑏 + 2𝑐)
4𝑎 + 4𝑏 + 2𝑐 ≠ 2𝑎 + 4𝑏 + 4𝑐
✓ * no es asociativo en z
CONMUTATIVO
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
2(𝑎 + 𝑏) = 2(𝑏 + 𝑎)
2𝑎 + 2𝑏 = 2𝑏 + 2𝑎
✓ * es conmutativo en Z
ELEMENTO NEUTRO
∀𝑎𝜖𝑍∃! 𝑒 ∈ 𝑅/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
DEMOSTRACION
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
2(𝑎 + 𝑒) = 𝑎 2(𝑒 + 𝑎) = 𝑎 2(𝑎 + 𝑒) = 2(𝑒 + 𝑎)
2𝑎 + 2𝑒 = 𝑎 2𝑒 + 2𝑎 = 𝑎

AL
2𝑒 = 𝑎 − 2𝑎 2𝑒 = 𝑎 − 2𝑎
𝑒 =
𝑎−2𝑎
2
𝑒 =
𝑎−2𝑎
2
𝑒 = −
𝑎
2
𝑒 = −
𝑎
2
2𝑎 + 2𝑒 = 𝑎 2𝑒 + 2𝑎 = 𝑎 2(𝑎 + 𝑒) = 2(𝑒 + 𝑎)
2𝑎 + 2(−
𝑎
2
) = 𝑎 2(−
𝑎
2
) + 2𝑎 = 𝑎 2 (𝑎 + (−
𝑎
2
)) = 2 ((−
𝑎
2
) + 𝑎)
2𝑎 − 𝑎 = 𝑎 −𝑎 + 2𝑎 = 𝑎 2𝑎 −
2𝑎
2
= −
2𝑎
2
+ 2𝑎
2𝑎 = 𝑎 + 𝑎 2𝑎 = 2𝑎 2𝑎 = 2𝑎
2𝑎 = 2𝑎
✓ * CUMPLE CON ELEMETO NEUTRO EN Z.
ELEMENTO SIMETRICO
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
2(𝑎 + 𝑎′) = −
𝑎
2
2(𝑎′
+ 𝑎) = −
𝑎
2
2(𝑎 + 𝑎′) = 2(𝑎′
+ 𝑎)
𝑎 + 𝑎′
= −
𝑎
4
𝑎′
+ 𝑎 = −
𝑎
4
𝑎′
= −
𝑎
4
− 𝑎 𝑎′
= −
𝑎
4
− 𝑎
2(𝑎 + 𝑎′) = −
𝑎
2
2(𝑎′
+ 𝑎) = −
𝑎
2
2(𝑎 + 𝑎′) = 2(𝑎′
+ 𝑎)
2 (𝑎 + (−
𝑎
4
− 𝑎)) = −
𝑎
2
2 ((−
𝑎
4
− 𝑎) + 𝑎) = −
𝑎
2
2(𝑎 + (−
𝑎
4
− 𝑎) = 2((−
𝑎
4
− 𝑎) + 𝑎)
2𝑎 −
2𝑎
4
− 2𝑎 = −
𝑎
2
−
2𝑎
4
− 2𝑎 + 2𝑎 = −
𝑎
2
2𝑎 −
2𝑎
4
− 2𝑎 = −
2𝑎
4
− 2𝑎 + 2𝑎
−
𝑎
2
= −
𝑎
2
−
𝑎
2
= −
𝑎
2
−
2𝑎
4
= −
2𝑎
4
= −
𝑎
2
= −
𝑎
2
✓ * TAMBIEN CUMPLE EN Z

AL
5. En ℤ, se define ⋇ por medio de a⋇b = a + b + 4. Estudiar sus propiedades.
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑍 / (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎 + 𝑏 + 4) ∗ 𝑐 = 𝑎 ∗ (𝑏 + 𝑐 + 4)
(𝑎 + 𝑏 + 4) + 𝑐 + 4 = 𝑎 + (𝑏 + 𝑐 + 4) + 4
𝑎 + 𝑏 + 𝑐 + 8 = 𝑎 + 𝑏 + 𝑐 + 8
✓ * CUMPLE LA ASOCITIVIDAD EN Z
CONMUTATIVO
∀𝑎, 𝑏𝜖𝑍/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
DEMOSTRACION
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
𝑎 + 𝑏 + 4 = 𝑏 + 𝑎 + 4
✓ * CUMPLE LA CONMUTATIVIDAD EN Z
ELEMENTO NEUTRO
∀𝑎𝜖𝑍∃! 𝑒 ∈ 𝑍/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
𝑎 + 𝑒 + 4 = 𝑎 𝑒 + 𝑎 + 4 = 𝑎 𝑎 + 𝑒 + 4 = 𝑒 + 𝑎 + 4
𝑒 = −4 𝑒 = −4
𝑎 + 𝑒 + 4 = 𝑎 𝑒 + 𝑎 + 4 = 𝑎 𝑎 + 𝑒 + 4 = 𝑒 + 𝑎 + 4
𝑎 + (−4) + 4 = 𝑎 −4 + 𝑎 + 4 = 𝑎 𝑎 + (−4) + 4 = −4 + 𝑎 + 4
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎
✓ * CUMPLE EL NEUTRO EN Z

AL
ELEMENTO SIMETRICO
∀𝑎𝜖𝑍+
∃! 𝑎′
/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
DEMOSTRACION
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎′
∗ 𝑎 = 𝑎′
∗ 𝑎
𝑎 + 𝑎′
+ 4 = −4 𝑎′
+ 𝑎 + 4 = −4 𝑎 + 𝑎′
+ 4 = 𝑎′
+ 𝑎 + 4
𝑎′
= −4 − 4 − 𝑎 𝑎′
= −4 − 4 − 𝑎
𝑎′
= −8 − 𝑎 𝑎′
= −8 − 𝑎
REEMPLAZANDO
𝑎 + 𝑎′
+ 4 = −4 𝑎′
+ 𝑎 + 4 = −4 𝑎 + 𝑎′
+ 4 = 𝑎′
+ 𝑎 + 4
𝑎 + (−8 − 𝑎) + 4 = −4 (−8 − 𝑎) + 𝑎 + 4 = −4 𝑎 + (−8 − 𝑎) + 4 = −8 − 𝑎 + 𝑎 + 4
𝑎 − 8 − 𝑎 + 4 = −4 −8 − 𝑎 + 𝑎 + 4 = −4 𝑎 − 8 − 𝑎 + 4 = −8 − 𝑎 + 𝑎 + 4
−4 = −4 −4 = −4 −4 = −4
✓ * CUMPLE LA SIMETRIA EN 𝑍+
6. Estudiar sus propiedades de ⨁: ℚ* x ℚ* → ℚ* / x⨁y= x + 1/y. Si ℚ* = ℚ - {0}
ASOCIATIVO
∀𝑥, 𝑦, 𝑧𝜖 ℚ − {0}/ (𝑥⨁𝑦)⨁𝑧 = 𝑥⨁(𝑦⨁𝑧)
DEMOSTRACION
(𝑥⨁𝑦)⨁𝑧 ≠ 𝑥⨁(𝑦⨁𝑧)
(𝑥 +
1
𝑦
) ⨁ z ≠ z⨁(y +
1
z
)
(𝑥 +
1
𝑦
) +
1
𝑧
≠ 𝑧 +
1
(y+
1
z
)
✓ NO ES ASOCIATIVO Q
CONMUTATIVO
∀𝑥, 𝑦𝜖ℚ − {0}/ 𝑥⨁y = 𝑦⨁𝑥
DEMOSTRACION
𝑥⨁y ≠ 𝑦⨁𝑥
𝑥 +
1
𝑦
≠ 𝑦 +
1
𝑥
✓ NO ES CONMUTATIVO Q

AL
ELEMENTO NEUTRO
∀𝑥𝜖𝑄 − {0}; ∃! 𝑒 ∈ 𝑄 − {0}/ 𝑥 ∗ 𝑒 = 𝑒 ∗ 𝑥 = 𝑥
𝑥 ∗ 𝑒 = 𝑥 𝑒 ∗ 𝑥 = 𝑥 𝑥 ∗ 𝑒 = 𝑒 ∗ 𝑥
𝑥 +
1
𝑒
= 𝑥
1
𝑒
= 0 …..no existe un elemento neutro.
ELEMENTO SIMETRICO
7. La función f: ℝ → ℝ es una ley de composición interna en ℝ definida por f(a,b) = a + b2. ¿Es
asociativo, conmutativo y/o admite?
(𝑓(𝑎) ∗ 𝑓(𝑏)) = 𝑓(𝑎, 𝑏)
SOLUCION
ASOCIATIVA
∀𝑓(𝑎), 𝑓(𝑏), 𝑓(𝑐)𝜖𝑅/ (𝑓(𝑎) ∗ 𝑓(𝑏)) ∗ 𝑓(𝑐) = 𝑓(𝑎) ∗ (𝑓(𝑏) ∗ 𝑓(𝑐))
(𝑓(𝑎) ∗ 𝑓(𝑏)) ∗ 𝑓(𝑐) = 𝑓(𝑎) ∗ (𝑓(𝑏) ∗ 𝑓(𝑐))
(𝑎 + 𝑏2) ∗ 𝑓(𝑐) ≠ 𝑓(𝑎) ∗ (𝑏 + 𝑐2
)
(𝑎 + 𝑏2) + 𝑐2
≠ 𝑎 + (𝑏 + 𝑐2
)2
∗ 𝑛𝑜 𝑐𝑢𝑚𝑝𝑙𝑖𝑟𝑖𝑎 𝑙𝑎 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑖𝑑𝑎𝑑
CONMUTATIVO
solucion
∀𝑓(𝑎), 𝑓(𝑏) ∈ 𝑅/𝑓(𝑎) ∗ 𝑓(𝑏) = 𝑓(𝑏) ∗ 𝑓(𝑎
DEMOSTACION
𝑓(𝑎) ∗ 𝑓(𝑏) = 𝑓(𝑏) ∗ 𝑓(𝑎)
𝑎 + 𝑏2
≠ 𝑏 + 𝑎2
∗ 𝑛𝑜 𝑐𝑢𝑚𝑝𝑙𝑒 𝑙𝑎 𝑐𝑜𝑛𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑖𝑑𝑎𝑑
8. En ℚ* se define ⋇ tal que a⋇b = 3ab. Verificar que ⋇ es asociativo, con elemento neutro,
conmutativo y además todos los elementos inversibles.
ASOCIATIVO
∀𝑎, 𝑏, 𝑐𝜖𝑄 − {0}/ (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
DEMOSTRACION
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
3𝑎𝑏 ∗ 𝑐 = 𝑎 ∗ 3𝑏𝑐
3(3𝑎𝑏𝑐) = 3(𝑎3𝑏𝑐)
9𝑎𝑏𝑐 = 9𝑎𝑏𝑐
✓ Cumple con la
asociatividad Q-{0}

AL
CONMUTATIVA
∀𝑎, 𝑏𝜖𝑄 − {0}/ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
DEMOSTRACION
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
3𝑎𝑏 = 3𝑏𝑎
✓ SI CUMPLE LA CONMUTATIVA EN Q-{0}
ELEMENTO NEUTRO
∀𝑎𝜖𝑄 − {0}, ∃! 𝑒 ∈ 𝑄 − {0}/ 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎
𝑎 ∗ 𝑒 = 𝑎 𝑒 ∗ 𝑎 = 𝑎 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎
3𝑎𝑒 = 𝑎 3𝑒𝑎 = 𝑎 3𝑎𝑒 = 3𝑒𝑎
𝑒 =
1
3
𝑒 =
1
3
3𝑎(
1
3
) = 𝑎 3(
1
3
)𝑎 = 𝑎 3𝑎(
1
3
) = 3(
1
3
)𝑎
𝑎 = 𝑎 𝑎 = 𝑎 𝑎 = 𝑎
✓ Cumple con la propiedad del elemento neutro en 𝑄 − {0}
ELEMENTO SIMETRICO
∀𝑎𝜖𝑄 − {0}∃! 𝑎′
∈ 𝑄 − {0}/ 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎 = 𝑒
𝑎 ∗ 𝑎′
= 𝑒 𝑎′
∗ 𝑎 = 𝑒 𝑎 ∗ 𝑎′
=𝑎′
∗ 𝑎
3𝑎𝑎′
=
1
3
3𝑎′
𝑎 =
1
3
𝑎′
=
1
9𝑎
𝑎′
=
1
9𝑎
Reemplazando
3𝑎(
1
9𝑎
) =
1
3
1
3
=
1
3
Por lo tanto tiene simetría en Q-{0}.

AL
9. En ℕ se definen las leyes de composición interna ⋇ y ⨁ mediante:
x ⋇ y = x
x ⨁ y = x + y Estudiar sus propiedades de ⋇
respecto de ⨁
SOLUCION
ASOCIATIVA
∀𝑥, 𝑦, 𝑧𝜖𝑁 /(𝑥 ∗ 𝑦)⨁𝑧 = 𝑥⨁(𝑦 ∗ 𝑧)
Demostración
(𝑥 ∗ 𝑦)⨁𝑧 = 𝑥⨁(𝑦 ∗ 𝑧)
𝑥⨁z = x⨁y
𝑥 + 𝑧 ≠ 𝑥 + 𝑦
∗ → ⨁
𝑛𝑜 𝑠𝑒𝑟𝑖𝑎 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑜
CONMUTATIVA
𝑥⨁y = y ⨁ 𝑥
𝑥 + 𝑦 = 𝑦 + 𝑥
Si cumpliría la conmutatividad
10. Crear una tabla de composición de funciones del conjunto A = {1,2,3} en sí mismo.
SOLUCION
𝐴𝑥𝐴−> 𝐴
𝐴 = {1,2,3}
𝐴 = {1 ,2,3}
A x A 1 2 3
1 (1,1) (1,2) (1,3)
2 (2,1) (2,2) (2,3)
3 ((3,1) (3,2) (3,3)
ELEMENTO NEUTRO
∀𝑥 ∈ 𝑁, ∃! 𝑒 ∈ 𝑁/ 𝑥 ∗ 𝑒 = 𝑒 ∗ 𝑥 = 𝑥
Demostración
𝑥 ∗ 𝑒 = 𝑒 ∗ 𝑥 = 𝑥
Reemplazando
𝑥 ∗ 𝑒 = 𝑥
𝑥 ∗ 𝑦 = 𝑥𝑥 = 𝑥
NO es tiene elemento neutro , por lo que se
considera
Que tampoco existe un elemento simétrico.

AL
11. Crear una tabla de composición de funciones del conjunto A = {a,b} en sí mismo
°
F1 F2 F3 F4
F1 A A a A
F2 A A b B
F3 B B b A
F4 B b b B
12. Sea U un conjunto universal. Sea P(U) la familia de todos los conjuntos de U. ¿La intersección,
unión, diferencia de conjuntos y diferencia simétrica se hallan totalmente definidas? ¿Por qué?
✓ Si es unión porque es subconjunto a otro subconjunto
∀a, b, c ∈ P(u)/ AuB =C⇒ C ∈ P(u)
✓ Intersección ∀a, b, c ∈ P(u)/ A∩B =C⇒ C ∈ P(u)
✓ Diferencia ∀a, b, c ∈ P(u)/ A−B =C⇒ C ∈ P(u)
Entonces concluiremos diciendo que si están definidas.
13. ¿La adición y sustracción de ángulos son leyes de composición interna? ¿Por qué?
Rpta: La adición y sustracción son leyes de composición interna, porque al sumar o restar
dichos ángulos se obtiene otro ángulo.
14. Sea S un conjunto con exactamente un elemento ¿Cuántas operaciones binarias diferentes
pueden definirse en S? Respóndase a la pregunta si S tiene 2 elementos, si tiene 3 elementos,
si tiene “n” elementos.
SOLUCION:
Con un elemento 1 …….necesariamente tendría que haber un elemento mas para poder
operar
Con dos elementos 2 …..se podria operad de dos maneras distintas
Con tres elementos 3 ……se odria operar de tres formas distintas
Con n elementos…………..se operaria de n formas.
𝐴𝑥𝐴−> 𝐴
𝐴 = {𝑎, 𝑏}
𝐴 = {𝑎, 𝑏}
𝐴𝑥𝐴 = {(𝑎, 𝑎)(𝑎, 𝑏)(𝑏, 𝑎)(𝑏, 𝑏)}
𝐹1 = {(𝑎, 𝑎)(𝑏, 𝑎)}
𝐹2 = {(𝑎, 𝑎)(𝑏, 𝑏)}
𝐹3 = {(𝑎, 𝑏)(𝑏, 𝑎)}
𝐹4 = {(𝑎, 𝑏)(𝑏, 𝑏)}
Evaluando con respecto a “a”.

AL
15. Pruébese que si ⋇ es una operación interna en un conjunto A, asociativa y conmutativa,
entonces (a⋇b) ⋇ (c⋇d) = [(d⋇c) ⋇ a] ⋇ b; ∀a,b,c,d ∈A. Supóngase que la ley asociativa se
cumple, como en la definición, sólo para ternas, esto es, supóngase sólo (x⋇y) ⋇ z = x⋇(y⋇z);
∀x,y,z ∈A
(a ⋇ b) ⋇ (c ⋇ d) = [(d ⋇ c) ⋇ a] ⋇ b
(a ⋇ b) ⋇ (d ⋇ c) = [(d ⋇ c) ⋇ a] ⋇ b conmutando
(d ⋇ c) ⋇ (a ⋇ b) = [(d ⋇ c) ⋇ a] ⋇ b conmutando
[(d ⋇ c) ⋇ a ] ⋇ b= [(d ⋇ c) ⋇ a] ⋇ b asociativa
16.Sea ∗ una operación binaria interna definida en ℚ por: 𝑎 ∗ 𝑏 = (𝑎2
− 𝑏)(𝑏2
− 𝑎): Hallar el valor de
verdad de las siguientes afirmaciones:
a) ∗ Es Conmutativa=(v)
SOLUCIÓN.
∀𝒂, 𝒃 ∈ ℚ 𝒂 ∗ 𝒃 = 𝒃 ∗ 𝒂
𝒂 ∗ 𝒃 = 𝒃 ∗ 𝒂
(𝑎2
− 𝑏)(𝑏2
− 𝑎) = (𝑏2
− 𝑎)(𝑎2
− 𝑏)
Conmutativa multiplicativa en los Q.
(𝑎2
− 𝑏)(𝑏2
− 𝑎) = (𝑎2
− 𝑏)(𝑏2
− 𝑎)
➢ 𝒆𝒔 𝒄𝒐𝒏𝒎𝒖𝒕𝒂𝒕𝒊𝒗𝒂.
b) ∃𝒌 ∈ ℚ (
𝟏
𝒌
) (𝒂 ∗ 𝒃) = (𝒌𝒂) ∗ 𝒃
SOLUCIÓN.
(
𝟏
𝒌
) (𝒂 ∗ 𝒃) = (𝒌𝒂) ∗ 𝒃 →(F)
(
1
𝑘
) (𝑎2
− 𝑏)(𝑏2
− 𝑎) = ((𝑘𝑎)2
− 𝑏)(𝑏2
− 𝑘𝑎)
(
1
𝑘
) (𝑎2
− 𝑏)(𝑏2
− 𝑎) = ((𝑘𝑎)2
− 𝑏)(𝑏2
− 𝑘𝑎)
(𝑎2
− 𝑏)(𝑏2
− 𝑎)
𝑘
= (𝑘2
𝑎2
− 𝑏)(𝑏2
− 𝑘𝑎)
➢ 𝒏𝒐 𝒔𝒐𝒏 𝒊𝒈𝒖𝒂𝒍𝒆𝒔.

AL
c) 4 ∗ (3 ∗ 1) = 32.252 = 𝑽
SOLUCIÓN:
4 ∗ ((32
− 1)(12
− 3))= 32.252
4 ∗ ((8)(−2))= 32.252
4 ∗−16 = 32.252
(42
− (−16))((−16)2
− 4) = 32.252
(16 + 16)(256 − 4) = 32.252
𝟑𝟐. 𝟐𝟓𝟐 = 𝟑𝟐. 𝟐𝟓𝟐
➢ 𝑬𝒔 𝒗𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐
17.En ℚse define la operación ∗ por:a ∗ b = ab + a − b. Hallar el valor de verdad de las siguientes
afirmaciones:
a) ∀𝒂, 𝒃, ∈ ℚ; (𝒂 ∗ 𝒃) ∈ ℚ
SOLUCIÓN:
(𝒂 ∗ 𝒃) ∈ ℚ
𝒂𝒃 + 𝒂 − 𝒃 ∈ ℚ
(𝒂𝒃 − 𝒃) + 𝒂 ∈ ℚ
𝒃(𝒂 − 𝟏) + 𝒂 ∈ ℚ
𝐋𝐚 𝐬𝐨𝐥𝐮𝐜𝐢𝐨𝐧 𝐩𝐞𝐫𝐭𝐞𝐧𝐞𝐜𝐞 𝐚 𝐥𝐨𝐬 ℚ
➢ 𝒗𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐.
b) ∗ 𝐞𝐬 𝐚𝐬𝐨𝐜𝐢𝐚𝐭𝐢𝐯𝐚.
SOLUCIÓN:
∀𝒂, 𝒃, 𝒄 ∈ ℚ (𝒂 ∗ 𝒃) ∗ 𝒄 = 𝒂 ∗ (𝒃 ∗ 𝒄).
(𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐)
(𝑎𝑏 + 𝑎 − 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏𝑐 + 𝑏 − 𝑐)
(𝑎𝑏 + 𝑎 − 𝑏)𝑐 + (𝑎𝑏 + 𝑎 − 𝑏) − 𝑐 = 𝑎(𝑏𝑐 + 𝑏 − 𝑐) + 𝑎 − (𝑏𝑐 + 𝑏 − 𝑐)
𝑎𝑏𝑐 + 𝑎𝑐 − 𝑏𝑐 + 𝑎𝑏 + 𝑎 − 𝑏 − 𝑐 = 𝑎𝑏𝑐 + 𝑎𝑏 − 𝑎𝑐 + 𝑎 − 𝑏𝑐 + 𝑏 − 𝑐
𝒂𝒄 − 𝒃 = −𝒂𝒄 + 𝒃
𝑬𝒔 𝒇𝒂𝒍𝒔𝒐, 𝑵𝒐 𝒆𝒔 𝒂𝒔𝒐𝒄𝒊𝒂𝒕𝒊𝒗𝒂.

AL
c) ∃! 𝒆 ∈ ℚ, 𝐞𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐧𝐞𝐮𝐭𝐫𝐨 𝐩𝐚𝐫𝐚 ∗
SOLUCIÓN:
∀𝒂, ∈ ℚ, ∃! 𝒆 ∈ ℚ 𝒂 ∗ 𝒆 = 𝒆 ∗ 𝒂 = 𝒂.
SOLUCIÓN:
𝒊) 𝒂 ∗ 𝒆 = 𝒂
𝑎𝑒 + 𝑎 − 𝑒 = 𝑎
𝑒(𝑎 − 1) = 1
𝒆 =
𝟏
(𝒂 − 𝟏)
∉ ℚ
𝒊𝒊) 𝒆 ∗ 𝒂 = 𝒂
𝑒𝑎 + 𝑒 − 𝑎 = 𝑎
𝑒(𝑎 + 1) = 2𝑎
𝒆 =
𝟐𝒂
𝒂 + 𝟏
∉ ℚ
𝒊𝒊𝒊) 𝒂 ∗ 𝒆 = 𝒆 ∗ 𝒂
𝑎𝑒 + 𝑎 − 𝑒 = 𝑒𝑎 + 𝑒 − 𝑎
𝒂 − 𝒆 ≠ 𝒆 − 𝒂
𝐍𝐨 𝐡𝐚𝐲 𝐞𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐧𝐞𝐮𝐭𝐫𝐨 𝐩𝐚𝐫𝐚 ∗
➢ 𝑬𝒔 𝒇𝒂𝒍𝒔𝒐.
d) 𝒄𝒂𝒅𝒂 𝒙 ∈ ℚ − {𝟏} 𝐩𝐨𝐬𝐞𝐞 𝐢𝐧𝐯𝐞𝐫𝐬𝐨 𝐩𝐚𝐫𝐚 ∗
∀𝒙, ∈ ℚ, ∃! 𝒙′ ∈ ℚ 𝒙 ∗ 𝒙′ = 𝒙′ ∗ 𝒙 = 𝒆.
SOLUCIÓN:
𝒊) 𝒙 ∗ 𝒙′ = 𝒆
𝑥𝑥′
+ 𝑥 − 𝑥′ =
1
(𝑥 − 1)
𝑥′(𝑥 − 1) =
1
(𝑥 − 1)
− 𝑥
𝑥′(𝑥 − 1) =
1
(𝑥 − 1)
− 𝑥(𝑥 − 1)
𝑥′(𝑥 − 1) =
1 − 𝑥2
+ 1
(𝑥 − 1)
𝒙′
=
𝟐 − 𝒙𝟐
(𝒙 − 𝟏)(𝒙 − 𝟏)
∈ ℚ − {𝟏}
➢ 𝐩𝐨𝐬𝐞𝐞 𝐞𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐢𝐧𝐯𝐞𝐫𝐬𝐨 𝐩𝐚𝐫𝐚 ∗
𝒊𝒊) 𝒙′
∗ 𝒙 = 𝒆
𝑥′
∗ 𝑥 = 𝑒

AL
𝑥′
𝑥 + 𝑥′
− 𝑥 =
2𝑥
𝑥 + 1
𝑥′(𝑥 + 1) =
2𝑥
(𝑥 + 1)
+ 𝑥
𝑥′(𝑥 + 1) =
2𝑥
(𝑥 + 1)
+ 𝑥(𝑥 + 1)
𝑥′
=
2𝑥 + 𝑥2
+ 1
(𝑥 + 1)(𝑥 + 1)
𝑥′
=
𝑥2
+ 2𝑥 + 1
(𝑥 + 1)(𝑥 + 1)
𝑥′
=
(𝑥 + 1)(𝑥 + 1)
(𝑥 + 1)(𝑥 + 1)
𝒙′
= 𝟏 ∉ ℚ − {𝟏}
➢ 𝐍𝐨 𝐩𝐨𝐬𝐞𝐞 𝐞𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐢𝐧𝐯𝐞𝐫𝐬𝐨 𝐩𝐚𝐫𝐚 ∗
𝒊𝒊𝒊) 𝒙′
∗ 𝒙 = 𝒙 ∗ 𝒙′
2 − 𝑥2
(𝑥 − 1)(𝑥 − 1)
∗ 𝑥 = 𝑥 ∗
2 − 𝑥2
(𝑥 − 1)(𝑥 − 1)
2 − 𝑥2
(𝑥 − 1)2
𝑥 +
2 − 𝑥2
(𝑥 − 1)2
− 𝑥 = 𝑥
2 − 𝑥2
(𝑥 − 1)2
+ 𝑥 − (
2 − 𝑥2
(𝑥 − 1)2
)
2𝑥 − 𝑥3
(𝑥 − 1)2
+
2 − 𝑥2
(𝑥 − 1)2
− 𝑥 =
2𝑥 − 𝑥3
(𝑥 − 1)2
+ 𝑥 − (
2 − 𝑥2
(𝑥 − 1)2
)
𝟐 − 𝒙𝟐
(𝒙 − 𝟏)𝟐
− 𝒙 = 𝒙 − (
𝟐 − 𝒙𝟐
(𝒙 − 𝟏)𝟐
) ∈ ℚ − {𝟏}
➢ 𝐏𝐨𝐬𝐞𝐞 𝐞𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐢𝐧𝐯𝐞𝐫𝐬𝐨 𝐩𝐚𝐫𝐚 ∗
18.En el conjunto A = {1;2;3;4} se define una operación ⋇ por medio de una tabla tal que,
los elementos de cada columna y cada fila son diferentes, tiene a 4 como elemento neutro
y cada elemento es su propio inverso. Determinar el valor de verdad de las siguientes
afirmaciones:
SOLUCIÓN:
⋇ 1 2 3 4
1 4 3 2 1
2 3 4 1 2
3 2 1 4 3
4 1 2 3 4

AL
a) (𝟐 ⋇ 𝟑) ⋇ (𝟐 ⋇ 𝟒) = 𝟐
SOLUCIÓN:
(𝟐 ⋇ 𝟑) ⋇ (𝟐 ⋇ 𝟒) = 𝟐
1 ⋇ 2 = 2
𝟑 ≠ 𝟐
➢ 𝐄𝐬 𝐟𝐚𝐥𝐬𝐨 𝐩𝐚𝐫𝐚 ∗
b) ⋇ 𝒆𝒔 𝒄𝒐𝒏𝒎𝒖𝒕𝒂𝒕𝒊𝒗𝒐
SOLUCIÓN:
➢ 𝐄𝐬 𝐜𝐨𝐧𝐦𝐮𝐭𝐚𝐭𝐢𝐯𝐚, 𝐩𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨 𝐞𝐬 𝐯𝐞𝐫𝐝𝐚𝐝𝐞𝐫𝐨
c) (𝟑 ⋇ 𝟐’ ) ⋇ 𝟑’ = 𝟐
SOLUCIÓN:
Calculemos la inversa.
𝟐 ⋇ 𝟐′
= 𝟒
𝟐 ⋇ 𝟐 = 𝟒
𝟑 ⋇ 𝟑′
= 𝟒
𝟑 ⋇ 𝟑 = 𝟒
(𝟑 ⋇ 𝟐’ ) ⋇ 𝟑’ = 𝟐
(𝟏 ) ⋇ 𝟑’ = 𝟐
(𝟏 ) ⋇ 𝟑’ = 𝟐
𝟐 = 𝟐
➢ 𝐄𝐬 𝐯𝐞𝐫𝐝𝐚𝐝𝐞𝐫𝐨
⋇ 1 2 3 4
1 4 3 2 1
2 3 4 1 2
3 2 1 4 3
4 1 2 3 4

AL
19.Sea ℚ* en donde se define la operación ⋇ por: a⋇b = 1/a + 1/b ¿Cuáles de las siguientes
afirmaciones son verdaderas?
a) Si a ⋇ (2/3) = 5 ⟶ ab = – 15/7
SOLUCIÓN:
a ⋇ (
2
3
) = 5
1
𝑎
+
1
(
2
3)
= 5
1
𝑎
+
3
2
= 5
2 + 3𝑎
2𝑎
= 5
2 + 3𝑎 = 10𝑎
2 = 7𝑎
2
7
= 𝑎
𝐏𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨:
𝐚𝐛 = –
𝟏𝟓
𝟕
.
b) ∀a,b ∈ℚ* / a⋇(b⋇c) = (a⋇b)⋇c
SOLUCIÓN:
𝑎 ⋇ (𝑏 ⋇ 𝑐) = (𝑎 ⋇ 𝑏) ⋇ 𝑐
𝑎 ⋇ (
1
𝑏
+
1
𝑐
) = (
1
𝑎
+
1
𝑏
) ⋇ 𝑐
𝑎 ⋇ (
𝑐 + 𝑏
𝑏𝑐
) = (
𝑏 + 𝑎
𝑎𝑏
) ⋇ 𝑐
1
𝑎
+
1
(
𝑐 + 𝑏
𝑏𝑐
)
=
1
(
𝑏 + 𝑎
𝑎𝑏
)
+
1
𝑐
1
𝑎
+
𝑏𝑐
𝑐 + 𝑏
=
𝑎𝑏
𝑏 + 𝑎
+
1
𝑐
1
𝑎
+
𝑏𝑐
𝑐 + 𝑏
=
𝑎𝑏
𝑏 + 𝑎
+
1
𝑐
𝑐 + 𝑏 + 𝑎𝑏𝑐
𝑎 (𝑐 + 𝑏)
=
𝑎𝑏𝑐 + 𝑏 + 𝑎
(𝑏 + 𝑎)𝑐
2
7
. b = – 15/7
2
7
. b = –
15
7
b = –
15
2
𝐏𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨:
𝐚𝐛 = – 𝟏𝟓/𝟕
2
7
. –
15
2
= – 15/7
–
15
7
= –
15
7
𝐏𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨 𝐞𝐬 𝐯𝐞𝐫𝐝𝐚𝐝𝐞𝐫𝐨

AL
𝑐 + 𝑏 + 𝑎𝑏𝑐
𝑎𝑐 + 𝑎𝑏
=
𝑎𝑏𝑐 + 𝑏 + 𝑎
𝑏𝑐 + 𝑎𝑐
(𝑏𝑐 + 𝑎𝑐)(𝑐 + 𝑏 + 𝑎𝑏𝑐) = (𝑎𝑏𝑐 + 𝑏 + 𝑎)(𝑎𝑐 + 𝑎𝑏)
𝑏𝑐𝑐 + 𝑏𝑐𝑏 + 𝑏𝑐𝑎𝑏𝑐 + 𝑎𝑐𝑐 + 𝑎𝑐𝑏 + 𝑎𝑐𝑎𝑏 = 𝑎𝑏𝑐𝑎𝑐 + 𝑏𝑎𝑐 + 𝑎𝑎𝑐 + 𝑎𝑏𝑐𝑎𝑏 + 𝑏𝑎𝑏 + 𝑎𝑎𝑏
𝑏𝑐𝑐 + 𝑏𝑐𝑏 + 𝑏𝑐𝑎𝑏𝑐 = 𝑎𝑏𝑐𝑎𝑏 + 𝑏𝑎𝑏 + 𝑎𝑎𝑏
𝒃𝒄𝟐
+ 𝒃𝟐
𝒄 + 𝒂𝒃𝟐
𝒄𝟐
= 𝒂𝟐
𝒃𝟐
𝒄 + 𝒂𝒃𝟐
+ 𝒂𝟐
𝒃
𝑷𝒐𝒓 𝒍𝒐 𝒕𝒂𝒏𝒕𝒐 𝒆𝒔 𝒇𝒂𝒍𝒔𝒐.
c) 𝒂 ⋇ 𝒂 = 𝒂 ⟷ 𝒂𝟐
= 𝟐
SOLUCIÓN:
𝑎 ⋇ 𝑎 = 𝑎
1
𝑎
+
1
𝑎
= 𝑎
𝑎 + 𝑎
𝑎2
= 𝑎
2𝑎
𝑎2
= 𝑎
2 = 𝑎2
2 = 2
20.Sean ⊠ y ⊗ operaciones definidas en ℤ por: 𝑎 ⊠ 𝑏 = (𝑏 – 𝑎) /2; 𝑎 ⊗ 𝑏 = (𝑎 +
𝑏) /2. Resolver la ecuación: 2 ⊠ (3 ⊗ 𝑥) = (𝑥 ⊗ 11) ⊠ 6
SOLUCIÓN:
2 ⊠ (3 ⊗ 𝑥) = (𝑥 ⊗ 11) ⊠ 6
2 ⊠
(3 + 𝑥)
2
=
(𝑥 + 11)
2
⊠ 6
(3 + 𝑥)
2
−
2
1
2
=
6
1
−
(𝑥 + 11)
2
2
(3 + 𝑥) − 4
2
2
=
12 − (𝑥 + 11)
2
2
(3 + 𝑥) − 4
4
=
12 − (𝑥 + 11)
4
(3 + 𝑥) − 4 = 12 − (𝑥
+ 11)
𝑥 − 1 = 1 − 𝑥
𝟐𝒙 = 𝟐
𝒙 = 𝟏

AL
21.En el conjunto ℚ, definimos las siguientes operaciones: 𝑎 ⊠ 𝑏 = (1/2)𝑎 + 3𝑏; 𝑎 ⊗
𝑏 = 3𝑎 + (3/2)𝑏; 𝑎 ⊛ 𝑏 = 5𝑎 – 3𝑏. 𝑺𝒊 𝒙 ⊠ 𝒙 = 𝟗, 𝒚 ⊗ 𝒚 = 𝟐𝟏. Hallar el valor
de 𝒙 ⊛ 𝒚.
SOLUCIÓN:
a) 𝒙 ⊠ 𝒙 = 𝟗
(
1
2
) 𝑥 + 3𝑥 = 9
𝑥
2
+ 3𝑥 = 9
𝑥 + 6𝑥
2
= 9
𝑥 + 6𝑥
2
= 9
𝑥 + 6𝑥 = 18
𝑥 =
18
7
22. Se define la operación ⊛ en ℚ por: 𝑎 ⊛ 𝑏 = 𝑎 + 𝑏 – 𝑎𝑏. Hallar el valor de verdad
de las siguientes afirmaciones:
a. El cero es el elemento neutro en ⊛
SOLUCIÓN
∀𝒂, ∈ ℚ, ∃! 𝒆 ∈ ℚ 𝒂 ⊛ 𝒆 = 𝒆 ⊛ 𝒂 = 𝒂.
i) 𝒂 ⊛ 𝒆 = 𝒂
𝑎 + 𝑒 − 𝑎𝑒 = 𝑎
𝑒 =
0
(1 − 𝑎)
𝑒 =
0
(1 − 𝑎)
ℚ 𝒚𝒂 𝒒𝒖𝒆 𝒂 ≠ 𝟏
𝑒 = 0
𝑬𝒔 𝒇𝒂𝒍𝒔𝒐, 𝒑𝒆𝒓𝒐 "𝒂" 𝒅𝒆𝒃𝒆 𝒔𝒆𝒓 𝒅𝒊𝒇𝒆𝒓𝒆𝒏𝒕𝒆 𝒂 𝟏
𝒆⊛𝒂=𝒂
𝑒 + 𝑎 − 𝑒𝑎 = 𝑎
𝑒 =
0
(1 − 𝑎)
∉ ℚ 𝒚𝒂 𝒒𝒖𝒆 𝒂 ≠ 𝟏
𝑒 = 0
𝑬𝒔 𝒇𝒂𝒍𝒔𝒐, 𝒑𝒆𝒓𝒐 "𝒂" 𝒅𝒆𝒃𝒆 𝒔𝒆𝒓 𝒅𝒊𝒇𝒆𝒓𝒆𝒏𝒕𝒆 𝒂 𝟏
𝒃). 𝒚 ⊗ 𝒚 = 𝟐𝟏.
3𝑦 + (
3
2
) 𝑦 = 21
3𝑦 +
3𝑦
2
= 21
6𝑦 + 3𝑦
2
= 21
6𝑦 + 3𝑦 = 42
9𝑦 = 42
𝑦 =
42
9
𝒄). 𝒙 ⊛ 𝒚.
5𝑥 – 3𝑦
5 (
18
7
) – 3 (
42
9
)
90
7
– 14
90
7
– 14
90 − 98
7
−𝟖
𝟕

AL
ii) 𝒂⊛𝒆=𝒆⊛𝒂
𝑎 + 𝑒 − 𝑎𝑒 = 𝑒 + 𝑎 − 𝑒𝑎
0 = 0
𝑬𝒔 𝒇𝒂𝒍𝒔𝒐
b. (𝒂 + 𝒃) ⊛ (𝒂 – 𝒃) = 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
SOLUCIÓN
(𝒂 + 𝒃) ⊛ (𝒂 – 𝒃) = 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
(𝑎 + 𝑏) + (𝑎 – 𝑏) − (𝑎 + 𝑏)(𝑎 – 𝑏) = 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
𝑎 + 𝑏 + 𝑎 − 𝑏 − (𝑎 + 𝑏)(𝑎 – 𝑏) = 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
2𝑎 − (𝑎2
− 𝑎𝑏 + 𝑎𝑏 − 𝑏2
) = 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
−𝑎2
+ 2𝑎 + 𝑏2
≠ 𝒂𝟐
+ 𝟐𝒂 – 𝟐𝒃𝟐
𝐏𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨 𝐞𝐬 𝐟𝐚𝐥𝐬𝐨
c. 𝑺𝒊 𝒙 ⊛ 𝟑 = 𝟔 ⟶ 𝒙 = – 𝟑/𝟐
SOLUCIÓN
𝒙 ⊛ 𝟑 = 𝟔
𝑥 + 3 − 𝑥3 = 6
𝑥 − 3𝑥 = 6 − 3
−2𝑥 = 6 − 3
𝑥 = −3/2
d. ⊛ es conmutativa
SOLUCIÓN
∀𝒂, 𝒃, ∈ ℚ 𝒂 ⊛ 𝒃 = 𝒃 ⊛ 𝒂
𝑎 + 𝑏 − 𝑎𝑏 = 𝑏 + 𝑎 – 𝑏𝑎
𝑎 + 𝑏 − 𝑎𝑏 = 𝑎 + 𝑏 – 𝑎𝑏
0 = 0
𝐄𝐬 𝐜𝐨𝐧𝐦𝐮𝐭𝐚𝐭𝐢𝐯𝐚, 𝐩𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨 𝐞𝐬 𝐯𝐞𝐫𝐝𝐚𝐝𝐞𝐫𝐨.

AL
23. Si en ℚ definimos la operación ⊛ por: 𝑎 ⊛ 𝑏 = 𝑎(1 – 2𝑏) + 𝑏. Se afirman:
a. ∀𝒂, 𝒃 ∈ ℚ, 𝒂 ⊛ 𝒃 = 𝒃 ⊛ 𝒂
SOLUCIÓN
𝒂 ⊛ 𝒃 = 𝒃 ⊛ 𝒂
𝑎(1 – 2𝑏) + 𝑏 = 𝑏(1 − 2𝑎) + 𝑎
𝑎 – 2𝑏𝑎 + 𝑏 = 𝑏 − 2𝑎𝑏 + 𝑎
𝑎𝑏 = 𝑎𝑏
𝐄𝐬 𝐜𝐨𝐧𝐦𝐮𝐭𝐚𝐭𝐢𝐯𝐚, 𝐩𝐨𝐫 𝐥𝐨 𝐭𝐚𝐧𝐭𝐨 𝐞𝐬 𝐯𝐞𝐫𝐝𝐚𝐝𝐞𝐫𝐨.
b. 0 𝑒𝑠 𝑙𝑎 𝑖𝑑𝑒𝑛𝑡𝑖𝑑𝑎𝑑 𝑝𝑎𝑟𝑎 ⊛ 𝑦 ∀𝑎 ∈ ℚ
SOLUCIÓN
∀𝒂, ∈ ℚ, ∃! 𝒆 ∈ ℚ 𝒂 ⊛ 𝒆 = 𝒆 ⊛ 𝒂 = 𝒂
i) 𝒂 ⊛ 𝒆 = 𝒂
𝑎(1 – 2𝑒) + 𝑒 = 𝑎
𝑎 – 2𝑒𝑎 + 𝑒 = 𝑎
– 2𝑒𝑎 + 𝑒 = 0
𝑒(– 2𝑎 + 1) = 0
𝑒 =
0
(– 2𝑎 + 1)
∉ ℚ
ii) 𝒆 ⊛ 𝒂 = 𝒂
𝑒(1 – 2𝑎) + 𝑎 = 𝑎
𝑒 – 2𝑎𝑒 + 𝑎 = 𝑎
– 2𝑒𝑎 + 𝑒 = 0
𝑒(– 2𝑎 + 1) = 0
𝑒 =
0
(– 2𝑎 + 1)
∉ ℚ
iii) 𝒂 ⊛ 𝒆 = 𝒆 ⊛ 𝒂
𝑎(1 – 2𝑒) + 𝑒 = 𝑒(1 – 2𝑎) + 𝑎
𝑎 – 2𝑒𝑎 + 𝑒 = 𝑒 – 2𝑎𝑒 + 𝑎
0=0
𝟎 𝒏𝒐 𝒆𝒔 𝒊𝒅𝒆𝒏𝒕𝒊𝒅𝒂𝒅 𝒑𝒂𝒓𝒂 ⊛, ∀𝒂 ∈ ℚ

AL
c. (1’ ⊛ 2)’ =
1
3
SOLUCIÓN
1(1 – 2.2 )′ + 2 =
1
3
1(−3)′ + 2 =
1
3
−1
3
+ 2 =
1
3
−1 + 6
3
=
1
3
5
3
≠
1
3
¿Cuáles de las afirmaciones son verdaderas? ¿Por qué?
a. Es verdadero, porque cumple la propiedad conmutativa.
b. No es verdadero porque, no cumple el elemento neutro en los Q
c. No es verdadero, porque no se cumple la igualdad.
24.En ℚ definimos la operación ⊛ por: 𝑎 ⊛ 𝑏 = 𝑎 + 𝑏 + (1/5)𝑎𝑏. ¿Cuáles de las
afirmaciones siguientes son verdaderas?
a. La operación ⊛ es conmutativa
SOLUCIÓN
∀𝒂, 𝒃 ∈ ℚ, 𝒂 ⊛ 𝒃 = 𝒃 ⊛ 𝒂
𝑎 ⊛ 𝑏 = 𝑏 ⊛ 𝑎
𝑎 + 𝑏 + (
1
5
) 𝑎𝑏 = 𝑏 + 𝑎 + (
1
5
) 𝑏𝑎
𝑎 + 𝑏 +
𝑎𝑏
5
= 𝑏 + 𝑎 +
𝑏𝑎
5
𝑎𝑏 = 𝑎𝑏
𝑺𝒊 𝒄𝒖𝒎𝒑𝒍𝒆 𝒍𝒂 𝒑𝒓𝒐𝒑𝒊𝒆𝒅𝒂𝒅 𝒄𝒐𝒏𝒎𝒖𝒕𝒂𝒕𝒊𝒗𝒂,
𝒑𝒐𝒓 𝒍𝒐 𝒕𝒂𝒏𝒕𝒐 𝒆𝒔 𝒗𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐.
b. La operación ⊛ es asociativa
SOLUCIÓN
∀𝒂, 𝒃, 𝒄 ∈ ℚ (𝒂 ⊛ 𝒃) ⊛ 𝒄 = 𝒂 ⊛ (𝒃 ⊛ 𝒄).
(𝑎 ⊛ 𝑏) ⊛ 𝑐 = 𝑎 ⊛ (𝑏 ⊛ 𝑐)

AL
(𝑎 + 𝑏 + (
1
5
) 𝑎𝑏) ⊛ 𝑐 = 𝑎 ⊛ (𝑏 + 𝑐 + (
1
5
) 𝑏𝑐)
(𝑎 + 𝑏 +
𝑎𝑏
5
) ⊛ 𝑐 = 𝑎 ⊛ (𝑏 + 𝑐 +
𝑏𝑐
5
)
(
5𝑎 + 5𝑏 + 𝑎𝑏
5
) + 𝑐 + (
1
5
) (
5𝑎 + 5𝑏 + 𝑎𝑏
5
) 𝑐 = 𝑎 + (
5𝑏 + 5𝑐 + 𝑏𝑐
5
) + (
1
5
) 𝑎 (
5𝑏 + 5𝑐 + 𝑏𝑐
5
)
5𝑎 + 5𝑏 + 𝑎𝑏
5
+ 𝑐 + (
5𝑎𝑐 + 5𝑏𝑐 + 𝑎𝑏𝑐
25
) = 𝑎 +
5𝑏 + 5𝑐 + 𝑏𝑐
5
+ (
5𝑏𝑎 + 5𝑐𝑎 + 𝑎𝑏𝑐
25
)
5𝑎 + 5𝑏 + 𝑎𝑏 + 5𝑐
5
+ (
5𝑎𝑐 + 5𝑏𝑐 + 𝑎𝑏𝑐
25
) =
5𝑎 + 5𝑏 + 5𝑐 + 𝑏𝑐
5
+ (
5𝑏𝑎 + 5𝑐𝑎 + 𝑎𝑏𝑐
25
)
5(𝑎 + 𝑏 + 𝑐) + 𝑎𝑏
5
+ (
5(𝑎𝑐 + 𝑏𝑐) + 𝑎𝑏𝑐
25
) =
5(𝑎 + 𝑏 + 𝑐) + 𝑏𝑐
5
+ (
5(𝑎𝑏 + 𝑎𝑐) + 𝑎𝑏𝑐
25
)
𝑁𝑜 𝑐𝑢𝑚𝑝𝑙𝑒 𝑙𝑎 𝑝𝑟𝑜𝑝𝑖𝑒𝑑𝑎𝑑 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣, 𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜 𝑒𝑠 𝑓𝑎𝑙𝑠𝑜.
c. 0 es el elemento neutro identidad
SOLUCIÓN
∀𝒂, ∈ ℚ, ∃! 𝒆 ∈ ℚ 𝒂 ⊛ 𝒆 = 𝒆 ⊛ 𝒂 = 𝒂
SOLUCIÓN
i) 𝒂 ⊛ 𝒆 = 𝒂
𝑎 + 𝑒 + (
1
5
) 𝑎𝑒 = 𝑎
𝑎 + 𝑒 +
𝑎𝑒
5
= 𝑎
5𝑎 + 5𝑒 + 𝑎𝑒
5
= 𝑎
5𝑎 + 5𝑒 + 𝑎𝑒 = 5𝑎
𝑒(5 + 𝑎) = 0
𝑒 =
0
(5 + 𝑎)
∉ ℚ, 𝒂 ≠ −𝟓
ii) 𝒆 ⊛ 𝒂 = 𝒂
𝑒 + 𝑎 + (
1
5
) 𝑒𝑎 = 𝑎
𝑒 + 𝑎 +
𝑒𝑎
5
= 𝑎
5𝑒 + 5𝑎 + 𝑒𝑎
5
= 𝑎
5𝑒 + 5𝑎 + 𝑒𝑎 = 5𝑎
𝑒(5 + 𝑎) = 0

AL
𝑒 =
0
(5 + 𝑎)
∉ ℚ, 𝒂 ≠ −𝟓
iii) 𝒂 ⊛ 𝒆 = 𝒆 ⊛ 𝒂
𝑎 + 𝑒 + (
1
5
) 𝑎𝑒 = 𝑒 + 𝑎 + (
1
5
) 𝑒𝑎
𝑎 + 𝑒 +
𝑎𝑒
5
= 𝑒 + 𝑎 +
𝑒𝑎
5
0 = 0
𝑵𝒐 𝒄𝒖𝒎𝒑𝒍𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒊𝒅𝒆𝒏𝒕𝒊𝒅𝒂𝒅 𝒑𝒂𝒓𝒂 ⊛
d. ∀𝒂 ∈ ℚ, ∃𝒂’ ∈ ℚ
∀𝒂, ∈ ℚ, ∃! 𝒂′ ∈ ℚ 𝒂 ⊛ 𝒂′ = 𝒂′ ⊛ 𝒂 = 𝒆
SOLUCIÓN
i) 𝒂 ⊛ 𝒂′ = 𝒆
𝑎 + 𝑎′ + (
1
5
) 𝑎𝑎′ =
0
(5 + 𝑎)
𝑎 + 𝑎′ +
𝑎𝑎′
5
=
0
(5 + 𝑎)
5𝑎 + 5𝑎′
+ 𝑎𝑎′
5
=
0
(5 + 𝑎)
𝑎′
(5 + 𝑎) =
0
(5 + 𝑎)
− 5𝑎
𝑎′
=
0
(5 + 𝑎)2
− 5𝑎, ∉ ℚ, 𝒂 ≠ −𝟓
ii) 𝒂′ ⊛ 𝒂 = 𝒆
𝑎′
+ 𝑎 + (
1
5
) 𝑎′𝑎 =
0
(5 + 𝑎)
𝑎′
+ 𝑎 +
𝑎′𝑎
5
=
0
(5 + 𝑎)
5𝑎′
+ 5𝑎 + 𝑎𝑎′
5
=
0
(5 + 𝑎)
𝑎′
(5 + 𝑎) =
0
(5 + 𝑎)
− 5𝑎

AL
𝑎′
=
0
(5 + 𝑎)2
− 5𝑎, ∉ ℚ, 𝒂 ≠ −𝟓
iii) 𝒂 ⊛ 𝒂′ = 𝒂′ ⊛ 𝒂
𝑎 + 𝑎′
+ (
1
5
) 𝑎𝑎′
= 𝑎′
+ 𝑎 + (
1
5
) 𝑎′𝑎
𝑎 + 𝑎′
+
𝑎𝑎′
5
= 𝑎′
+ 𝑎 +
𝑎′𝑎
5
0 = 0
𝑵𝒐 𝒄𝒖𝒎𝒑𝒍𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒔𝒊𝒎𝒆𝒕𝒓𝒊𝒄𝒐 𝒑𝒂𝒓𝒂 ⊛
25.En el conjunto A = {1;2;3;4} definimos la operación ⊛ tal que 3 es la identidad, cada
elemento es su propio inverso y los elementos (dé los resultados en una tabla) de cada
fila y cada columna son diferentes. Si a es la solución de la ecuación (x⊛3)’ = (2⊛4’)’
; hallar el valor de: [(a⊛2)’ ⊛ (a’ ⊛ 3’)] ’
SOLUCIÓN
⊛ 1 2 3 4
1 3 4 1 2
2 4 3 2 1
3 1 2 3 4
4 2 1 4 3
(𝒙 ⊛ 𝟑)’ = (𝟐 ⊛ 𝟒’)′
(𝑥 ⊛ 3)’ = (2 ⊛ 4)′
(𝑥 ⊛ 3)’ = (1)′
(𝑥 ⊛ 3)’ = 3
Cuando “x”=3
(3 ⊛ 3)’ = 3
(3)’ = 3
3 = 3
hallar el valor de: [(𝑎 ⊛ 2)’ ⊛ (𝑎’ ⊛ 3’)] ’
reemplazamos “3” en a
[(3 ⊛ 2)’ ⊛ (3′ ⊛ 3′)] ’
[(2)’ ⊛ (3 ⊛ 3)] ’
[(2) ⊛ (3)] ’
[2] ’
2.

AL
Por lo tanto, x=3
26.Si en ℚ definimos la operación ⊛ por: 𝑎 ⊛ 𝑏 = 𝑎(1 – 2𝑏) + 𝑏. ¿Cuáles de las
a. 2’ ⊛ 1’ = 1/3
SOLUCIÓN
2’ ⊛ 1’ =
1
3
1
2
⊛ 1 =
1
3
1
2
(1 − 2.1) + 1 =
1
3
1
2
(1 − 2) + 1 =
1
3
b. ∀𝒂, 𝒃, 𝒄 ∈ ℚ; (𝒂 ⊛ 𝒃) ⊛ 𝒄 = 𝒂 ⊛ (𝒃 ⊛ 𝒄)
SOLUCIÓN
(𝒂 ⊛ 𝒃) ⊛ 𝒄 = 𝒂 ⊛ (𝒃 ⊛ 𝒄)
( 𝑎(1 – 2𝑏) + 𝑏) ⊛ 𝑐 = 𝑎 ⊛ ( 𝑏(1 – 2𝑐) + 𝑐)
( 𝑎 − 2𝑎𝑏 + 𝑏) ⊛ 𝑐 = 𝑎 ⊛ ( 𝑏 − 2𝑏𝑐 + 𝑐)
( 𝑎 − 2𝑎𝑏 + 𝑏)(1 − 2𝑐) + 𝑐 = 𝑎 (1 − 2(𝑏 − 2𝑏𝑐 + 𝑐 ) + ( 𝑏 − 2𝑏𝑐 + 𝑐))
( 𝑎 − 2𝑎𝑏 + 𝑏)(1 − 2𝑐) + 𝑐 = 𝑎 (1 − 2𝑏 + 4𝑏𝑐 − 2𝑐 ) + ( 𝑏 − 2𝑏𝑐 + 𝑐))
( 𝑎 − 2𝑎𝑏 + 𝑏)(1 − 2𝑐) + 𝑐 = 𝑎 (1 − 2𝑏 + 4𝑏𝑐 − 2𝑐 ) + ( 𝑏 − 2𝑏𝑐 + 𝑐))
𝑎 − 2𝑎𝑐 − 2𝑎𝑏 + 4𝑎𝑏𝑐 + 𝑏 − 2𝑏𝑐 + 𝑐 = 𝑎 − 2𝑎𝑏 + 4𝑎𝑏𝑐 − 2𝑎𝑐 + 𝑏 − 2𝑏𝑐 + 𝑐
𝑎𝑏𝑐 = 𝑎𝑏𝑐
𝑬𝒔 𝒗𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐.
c. (𝟐𝒙) ⊛ 𝟑 = 𝟐 ⊛ (𝟑𝒙) ⟶ 𝒙 = 𝟏
SOLUCIÓN
2𝑥(1 – 2.3) + 3 = 2(1 – 2.3𝑥) + 3𝑥
2𝑥(1 – 6) + 3 = 2(1 – 6𝑥) + 3𝑥
2𝑥 − 12 + 3 = 2 − 12𝑥 + 3𝑥
2𝑥 − 9 = 2 − 9𝑥
11𝑥 = 11
𝑥 = 1
𝑬𝒔 𝒗𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐.
−1
2
+ 1 =
1
3
−1 + 2
2
=
1
3
1
2
≠
1
3
𝑬𝒔 𝒇𝒂𝒍𝒔𝒐

AL
27.Sea ⊛una operación en ℚ. Si (2a+1)⊛(b – 2) = 2a + b + 1, hallar (- 3)’ ⊛ 4 .
SOLUCIÓN
(𝟐𝒂 + 𝟏) ⊛ (𝒃 – 𝟐) = 𝟐𝒂 + 𝒃 + 𝟏
❖ 𝑥 = 2𝑎 + 1
𝑥 − 1
2
= 𝑎
➢ 𝑦 = 𝑏 – 2
𝑦 + 2 = 𝑏
𝑥 ⊛ 𝑦 = 2𝑎 + 𝑏 + 1
𝑥 ⊛ 𝑦 = 2 (
𝑥 − 1
2
) + 𝑦 + 2 + 1
𝑥 ⊛ 𝑦 = 2 (
𝑥 − 1
2
) + 𝑦 + 2 + 1
𝑥 ⊛ 𝑦 = 𝑥 − 1 + 𝑦 + 2 + 1
𝑥 ⊛ 𝑦 = 𝑥 + 𝑦 + 2
i) 𝒙 ⊛ 𝒆 = 𝒆 ⊛ 𝒙
SOLUCIÓN
𝑥 + 𝑒 + 2 = 𝑒 + 𝑥 + 2
0 = 0
ii) 𝑰𝒏𝒗𝒆𝒓𝒔𝒐 𝒅𝒆 (−𝟑): 𝒂 ⊛ 𝒂′ = 𝒆
−3 ⊛ −3′ = −2
−3 + −3′
+ 2 = −2
−3 + −3′
= −4
−3′
= −1
(− 3)’ ⊛ 4
−1 ⊛ 4
−1 + 4 + 2
𝟓
Desarrollamos el inverso a
través de:
∀𝒙, ∈ ℚ, ∃! 𝒆 ∈ ℚ/ 𝒙 ⊛ 𝒆
= 𝒆 ⊛ 𝒙 = 𝒙
i) 𝒙 ⊛ 𝒆 = 𝒙
SOLUCIÓN
𝑥 + 𝑒 + 2 = 𝑥
𝑒 = −2
ii) 𝒆 ⊛ 𝒙 = 𝒙
SOLUCIÓN
𝑒 + 𝑥 + 2 = 𝑥
𝑒 = −2

AL
28.Si definimos la operación ⊛ en ℚ por: 𝑎 ⊛ 𝑏 = 𝑎 + 𝑏 – 𝑎𝑏 y si a’ es el inverso de a,
entonces hallar 2’ ⊛ 3’.
SOLUCIÓN
2’ ⊛ 3’
1
2
+
1
3
−
1
2
∗
1
3
3 + 2
6
−
1
6
5
6
−
1
6
𝟐
𝟑
Elemento Simetría.
i) 𝒂′ ⊛ 𝒂 = 𝒆
2 ⊛ 2′
=
0
(1– 𝑎)
∉ ℚ,𝑎 ≠ 1
2 + 2′
− 2.2′ =
0
(1– 𝑎)
2′
(1 − 2) =
0
(1– 𝑎)
− 2
2′(−1) = −2
2′
= 2
ii) 𝒂′ ⊛ 𝒂 = 𝒆
3 ⊛ 3′
=
0
(1– 𝑎)
∉ ℚ,𝑎 ≠ 1
3 + 3′
− 3.3′ =
0
(1– 𝑎)
3′
(1 − 3) =
0
(1– 𝑎)
− 3
3′(−2) = −3
𝟑′
=
𝟑
𝟐
Elemento Neutro.
i) 𝒂 ⊛ 𝒆 = 𝒂
𝑎 + 𝑒 – 𝑎𝑒 = 𝑎
𝑒 (1– 𝑎) = 0
𝑒 =
0
(1– 𝑎)
∉ ℚ, 𝑎 ≠ 1
REEMPLAZANDO:
2’ ⊛ 3’
2 +
3
2
− 2 ∗
3
2
2 +
3
2
− 3
7 − 6
2
𝑹𝑬𝑺𝑷𝑼𝑬𝑺𝑻𝑨:
𝟏
𝟐

AL
29. Sea A = {a;b;c;d} y ⊛ la operación definida en A mediante la tabla adjunta. Hallar:
x = [(d⊛a’ )’ ⊛ b’ ]’
Si es conmutativa ⊛
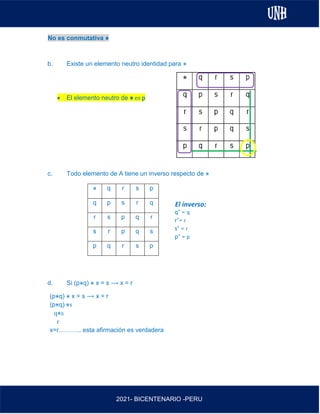
30.Si A = {p;q;r;s}, se define la operación ⋇ mediante la tabla adjunta. ¿Cuántas de las siguientes
a. ⋇ es conmutativa.
⊛ a b c d
a a b c d
b b a d c
c c d a b
d d c b a
⋇ q r s p
q p s r q
r s p q r
s r p q s
p q r s p
➢ Primero para poder resolver este ejercicio
tenemos que identificar tres cosa:
1) conmutativa
2) elemento neutro e=a
3) a⊛a’=e
a⊛a=a
b⊛b =a
c⊛ c=a
d⊛ d=a
a’=a
b’=b
c’=c
d’=d
𝑝 ∗ 𝑞 = 𝑞 ∗ 𝑝
𝑞 = 𝑞………son iguales
𝑞 ∗ 𝑟 = 𝑟 ∗ 𝑞
𝑠 = 𝑠..……son iguales
𝑟 ∗ 𝑠 = 𝑠 ∗ 𝑟
𝑝 = 𝑞….no son iguales
𝑝 ⊛ 𝑞 = 𝑞 ⊛ 𝑝
𝑏 = 𝑏……….son iguales
𝑏 ⊛ c = 𝑐 ⊛ b
𝑑 = 𝑑..……son iguales
𝑐 ⊛ 𝑑 = 𝑑 ⊛ c
𝑏 = 𝑏……. son iguales
x = [(d⊛a’)’ ⊛ b’ ]’
x= [(d⊛a)’ ⊛ b’ ]’
x= [d’ ⊛ b’ ]’
x= [d ⊛ b ]’
x= c’
x=c

AL
No es conmutativa ⋇
b. Existe un elemento neutro identidad para ⋇
• El elemento neutro de ⋇ es p
c. Todo elemento de A tiene un inverso respecto de ⋇
d. Si (p⋇q) ⋇ x = s ⟶ x = r
⋇ q r s p
q p s r q
r s p q r
s r p q s
p q r s p
(p⋇q) ⋇ x = s ⟶ x = r
(p⋇q) ⋇s
q⋇s
r
x=r……….. esta afirmación es verdadera
El inverso:
q’ = q
r’= r
s’ = r
p’ = p

AL
31.Sea A = {a;b;c;d;e} y ⋇ una operación binaria asociativa definida en A según el cuadro adjunto.
Dado el sistema de ecuaciones: x⋇y = b, x⋇y’ = d.
Hallar el par ordenado: (x⋇d;y⋇c)
SOLUCION
𝑥 ∗ 𝑦 = 𝑏
𝑥 ∗ 𝑦′
= 𝑑
Si tenemos lo siguiente
𝒙 ∗ 𝒅; 𝒚 ∗ 𝒄
Diremos que
𝒙 = 𝒂, 𝒃, 𝒄, 𝒅, 𝒆
𝒚 = 𝒂, 𝒃, 𝒄, 𝒅, 𝒆
𝒄 ∗ 𝒅; 𝒆 ∗ 𝒄
Si buscamos en el cuadro
(𝒄 ∗ 𝒅; 𝒆 ∗ 𝒄)
(𝒂; 𝒃) ………este seria el par que se estaría buscando.
⋇ a b c d e
a a b c d e
b b c d e a
c c d e a b
d d e a b c
e e a b c d
----------------------------------------------------------------
Se puede observar que en el cuadro se cumple la
conmutativa
Y se tiene como elemento neutro a:
e = a
-------------------------------------------------------------------------
𝑎 ∗ 𝑎′
= 𝑒
𝑎 ∗ 𝑎 = 𝑎
𝑏 ∗ 𝑒 = 𝑎
𝑑 ∗ 𝑐 = 𝑎
𝑒 ∗ 𝑏 = 𝑎
𝑎′ = 𝑒
𝑏′ = 𝑒
𝑐′
= 𝑑
𝑑′ = 𝑐
𝑒′ = 𝑏
𝑋 = 𝑐
𝑌 = 𝑒

AL
32.En el conjunto A = {p;q;r;s;t}, sea la operación definida en A, según lo indica el cuadro
adjunto. Si (p x’)’ (t q’) = t’.
Hallar el valor de: x r
SOLUCION
𝑎 ∗ 𝑎′
= 𝑒
𝑝 ∗ 𝑞 = 𝑠
𝑟 ∗ 𝑡 = 𝑠
𝑠 ∗ 𝑠 = 𝑠
𝑡 ∗ 𝑟 = 𝑠
33.Completar la siguiente tabla, de manera que se defina una operación binaria conmutativa en
S = {a,b,c,d}
p q r s t
p r s t p q
q s t p q r
r t p q r s
s p q r s t
t q r s t p
a b c d
a a b c d
b b d a c
c c a d b
d d c b a
𝑏 ⋇ 𝑐 = 𝑐 ⋇ 𝑏
𝑎 = 𝑎 … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
𝑐 ⋇ 𝑑 = 𝑑 ⋇ 𝑐
𝑏 = 𝑏 … … . . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
𝑏 ⋇ 𝑑 = 𝑑 ⋇ 𝑏
𝑐 = 𝑐 … … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
Podemos decir de que el operador * es
conmutativo y su elemento neutro es :
e= s
Entonces
. 𝑆𝑖 (𝑝 𝑥’)’ (𝑡 𝑞’) = 𝑡’
(𝑝 ∗ 𝑥′)′
∗ (𝑡 ∗ 𝑞′) = 𝑡′
(𝑝 ∗ 𝑥′) ∗ (𝑡 ∗ 𝑝) = 𝑟
(𝑝 ∗ 𝑥′) ∗ 𝑞 = 𝑟
Reemplazando
((𝑝 ∗ 𝑞′)´ ∗= 𝑟
(𝑝 ∗ 𝑝)′ ∗ 𝑞 = 𝑟
(𝑟)′
∗ 𝑞 = 𝑟
𝑡 ∗ 𝑞 = 𝑟
𝑟 = 𝑟
Si nos fijamos en la tabla
r con r resulta q
por lo que podemos decir que
x=q
AHORA REEMPLAZANDO
EN x r
q r esta operación nos da p.
entonces el valor que
buscamos es P.

AL
34.En la siguiente tabla completar, de tal manera la operación binaria es asociativo en S =
{a,b,c,d} Supóngase que esto es posible.
35. Sea la operación ⋇ definida en S = {a, b, c, d, e}, mediante la tabla que se muestra. Encontrar:
⋇ a b c d e
a a b c d e
b b c d e a
c c d e a b
d d e a b c
e e a b c d
1. 𝑏 ⋇ 𝑎 = 𝑏
2. 𝑑 ⋇ 𝑑 = 𝑒
3. 𝑐 ⋇ 𝑐 = 𝑒
4. 𝑒 ⋇ 𝑐 = 𝑏
5. 𝑎 ⋇ 𝑏 = 𝑏
6. 𝑏 ⋇ 𝑏 = 𝑐
7. 𝑏 ⋇ 𝑒 = 𝑎
8. [(𝑎 ⋇ 𝑐) ⋇ 𝑒] ⋇ 𝑎
a b c d
a a b c d
b b a c d
c c d c d
d d c c d
(𝑑 ⋇ 𝑎) ⋇ 𝑏 = 𝑑 ⋇ (𝑎 ⋇ 𝑏)
𝑑 ⋇ 𝑏 = 𝑑 ⋇ 𝑏
𝑐 = 𝑐 … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
(𝑏 ⋇ 𝑑) ⋇ 𝑐 = 𝑏 ⋇ (𝑑 ⋇ 𝑐)
𝑑 ⋇ 𝑐 = 𝑏 ⋇ 𝑐
𝑐 = 𝑐 … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
(𝑐 ⋇ 𝑏) ⋇ 𝑎 = 𝑐 ⋇ (𝑏 ⋇ 𝑎)
𝑑 ⋇ 𝑎 = 𝑐 ⋇ 𝑏
𝑑 = 𝑑 … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
(𝑐 ⋇ 𝑏) ⋇ 𝑑 = 𝑐 ⋇ (𝑏 ⋇ 𝑑)
𝑑 ⋇ 𝑑 = 𝑐 ⋇ 𝑑
𝑑 = 𝑑 … … . 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠.
[(𝑎 ⋇ 𝑐) ⋇ 𝑒] ⋇ 𝑎 = [𝑐 ⋇ 𝑒] ⋇ 𝑎 = 𝑏 ⋇ 𝑎 = 𝑏 𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑏
9. (𝑎 ⋇ 𝑏) ⋇ 𝑐 𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛
(𝑎 ⋇ 𝑏) ⋇ 𝑐 = 𝑏 ⋇ 𝑐 = 𝑑 𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑑
10. 𝑎 ⋇ (𝑏 ⋇ 𝑐) 𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛 𝑎 ⋇ (𝑏 ⋇ 𝑐) = 𝑎 ⋇ 𝑑 = 𝑑 𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑑
11. ¿ 𝑆𝑒 𝑝𝑢𝑒𝑑𝑒 𝑑𝑒𝑐𝑖𝑟, 𝑐𝑜𝑛 𝑏𝑎𝑠𝑒 𝑒𝑛 𝑒𝑠𝑡𝑒 𝑐á𝑙𝑐𝑢𝑙𝑜 (9 𝑦
10) 𝑞𝑢𝑒 ⋇ 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑜?
𝐸𝑠 𝐴𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎 (𝑎 ⋇ 𝑏) ⋇ 𝑐 = 𝑎 ⋇ (𝑏 ⋇ 𝑐) 𝑏 ⋇ 𝑐 = 𝑎 ⋇ 𝑑
𝑑 = 𝑑
𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜, 𝑠𝑖 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎
12. (𝑏 ⋇ 𝑑) ⋇ 𝑐
𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛
(𝑏 ⋇ 𝑑) ⋇ 𝑐 = 𝑒 ⋇ 𝑐 = 𝑏
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑏
13. 𝑏 ⋇ (𝑑 ⋇ 𝑐) 𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛 𝑏 ⋇ (𝑑 ⋇ 𝑐) = 𝑏 ⋇ 𝑎 = 𝑏 𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑏
14. ¿ 𝑆𝑒 𝑝𝑢𝑒𝑑𝑒 𝑑𝑒𝑐𝑖𝑟, 𝑐𝑜𝑛 𝑏𝑎𝑠𝑒 𝑒𝑛 𝑒𝑠𝑡𝑒 𝑐á𝑙𝑐𝑢𝑙𝑜 (12 𝑦 13), 𝑞𝑢𝑒
⋇ 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑜?
𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛
(𝑏 ⋇ 𝑑) ⋇ 𝑐 = 𝑏 ⋇ (𝑑 ⋇ 𝑐) 𝑒 ⋇ 𝑐 = 𝑏 ⋇ 𝑎
𝑏 = 𝑏
𝑝𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜, 𝑠𝑖 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎
15. ¿ 𝐴𝑐𝑎𝑠𝑜 ⋇ 𝑒𝑠 𝑐𝑜𝑛𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑜? ¿ 𝑃𝑜𝑟 𝑞𝑢é?
𝑆𝑖 𝑒𝑠 𝑎𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎 𝑝𝑜𝑟 𝑞𝑢𝑒 𝑐𝑢𝑚𝑝𝑙𝑒 𝑙𝑎 𝑖𝑔𝑢𝑎𝑙𝑑𝑎𝑑 𝑒𝑛 𝑎𝑚𝑏𝑜𝑠 𝑝𝑎𝑟𝑡𝑒𝑠.

AL
GRACIAS

Ley de composición interna algebra ii

More Related Content

What's hot

Similar to Ley de composición interna algebra ii

Recently uploaded

Ley de composición interna algebra ii