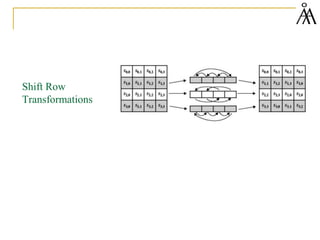
The document summarizes a lecture on the Advanced Encryption Standard (AES). AES was selected by the National Institute of Standards and Technology (NIST) in 2001 to replace the Data Encryption Standard (DES). AES is a symmetric block cipher that uses 128-bit blocks and 128/192/256-bit keys. The AES algorithm is based on Rijndael, designed by Joan Daemen and Vincent Rijmen. Rijndael uses a series of transformations including byte substitution, shifting rows of the state array, mixing data within columns, and combining the state array with the round key. These transformations are repeated over 10-14 rounds depending on the key size. The algorithm was chosen for its security, performance,




























![January 26, 2012 33
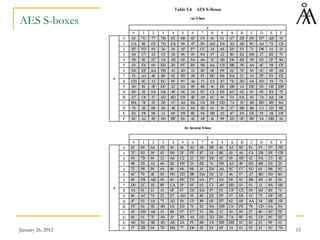
AES Key Expansion
Takes 128-bit (16-byte) key and expands into an array of 44 32-bit words
(each word has 4 bytes)
KeyExpansion(byte key[16], word w[44])
{
Word temp;
For (i=0;i<4; i++) // key is copied into the first 4 words
w[i]=(key[4*i], key[4*i+1],key[4*i+2],key[4*i+3])
For (i=4;i<44;i++) // the rest of the words are produced here
{
temp=w[i-1];
if (i mod 4 == 0)
temp=SubWord( RotWord(temp) ) ⊕ Rcon[i/4];
w[i]=w[i-4] ⊕ temp; // Most of the words are just XOR of two earlier values
}
}
http://users.abo.fi/ipetre/crypto/](https://image.slidesharecdn.com/lecture6-230423102011-efbad4a1/85/lecture6-pdf-31-320.jpg)
![January 26, 2012 34
AES key expansion
Key is copied first into the first 4 words of the expanded key
Each added word depends on the previous word and on the one 4 positions
earlier
In 3 cases out of 4 a simple XOR is used
For every fourth word a more complex function is used
RotWord performs one-byte circular left-shift on a word: [b0,b1,b2,b3] is
transformed into [b1,b2,b3,b0]
SubWord performs a byte substitution on each byte of the input word, using the
S-box of AES
Results of step 1 and 2 are XORED with a round constant Rcon[j] (a geometric
progression with rate 2 computed in GF(28):
J 1 2 3 4 5 6 7 8 9 10
Rcon[J] {01} {02} {04} {08} {10} {20} {40} {80} {1B} {36}
http://users.abo.fi/ipetre/crypto/](https://image.slidesharecdn.com/lecture6-230423102011-efbad4a1/85/lecture6-pdf-32-320.jpg)



