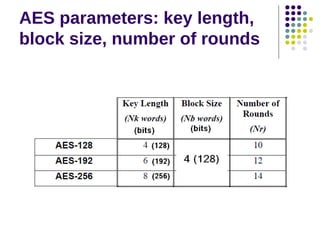
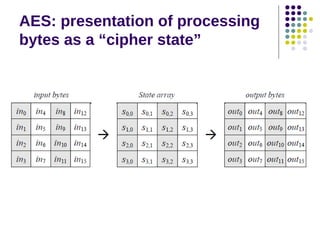
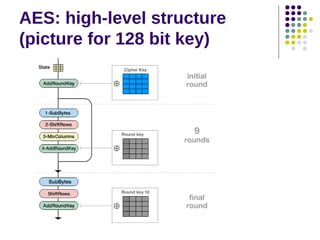
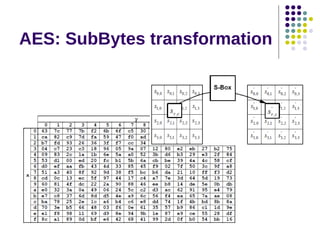
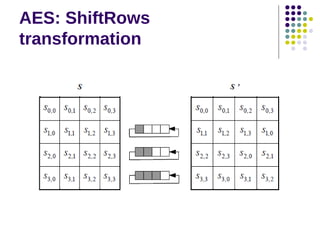
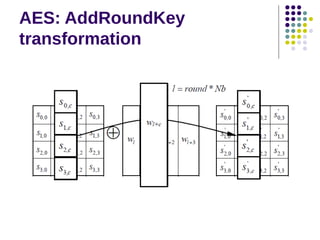
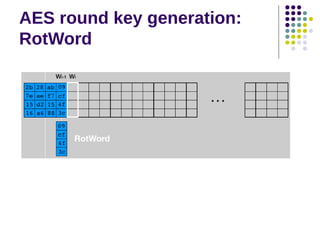
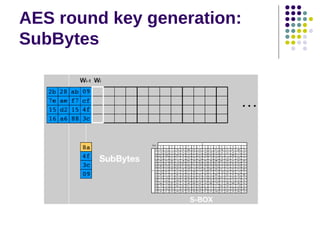
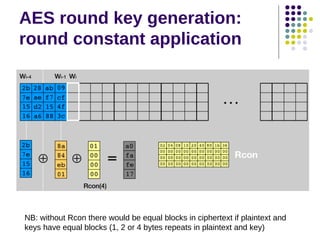
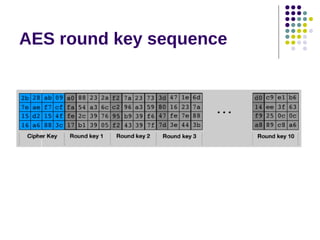
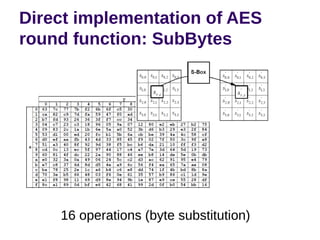
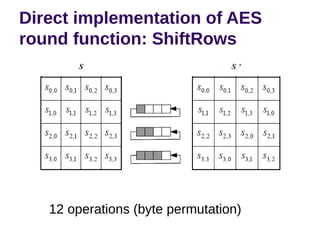
The document discusses effective software implementation of the Advanced Encryption Standard (AES), developed from the Rijndael cipher and selected in a cryptographic competition between 1997 and 2000. It covers AES properties, direct implementation challenges, optimization methods, and its efficiency on 32-bit platforms. The text concludes that effective AES implementation can significantly reduce processing time through look-up table accesses while maintaining cryptographic security.

1. Effective Software
Implementation of
Advanced Encryption Standard
December 2014
Roman Oliynykov
Professor at
Information Technologies Security Department
Kharkov National University of Radioelectronics
Head of Scientific Research Department
JSC “Institute of Information Technologies”
Ukraine
Visiting professor at
Samsung Advanced Technology Training Institute
Korea
ROliynykov@gmail.com

2. Outline
 A few words about myself
 Brief history of AES/Rijndael
 AES properties
 Direct AES implementation and problems with it
 Methods for effective encryption
implementation (proposed by Rijndael authors
in their submission to AES competition)
 Decryption optimization
 Conclusions

3. About myself (I)
 I’m from Ukraine (Eastern part of
Europe),
host country of Euro2012 football
championship
 I live in Kharkov (the second biggest
city in the country, population is 1.5
million people), Eastern Ukraine
(near Russia),
former capital of the Soviet Ukraine
(1918-1934)
three Nobel prize winners worked at
Kharkov University

4. About myself (II)
 Professor at Information Technologies Security
Department at Kharkov National University of
Radioelectronics
 courses on computer networks and operation
system security, special mathematics for
cryptographic applications
 Head of Scientific Research Department at JSC
“Institute of Information Technologies”
 Scientific interests: symmetric cryptographic
primitives synthesis and cryptanalysis
 Visiting professor at Samsung Advanced
Technology Training Institute
 courses on computer networks and operation
system security, software security, effective
application and implementation of symmetric
cryptography

5. Modern and effective solution:
Advanced Encryption Standard (AES)
 result of international public cryptographic competition
(1997-2000)
 had been chosen among 15 candidate ciphers
(developed in the US, Belgium, Denmark, Germany,
Israel, Japan, Switzerland, Armenia, etc.)
 original name is Rijndael (developed by researchers from
Belgium)
 votes on 3rd AES conference had been given to this
cipher, but the rest Twofish (US), MARS (US, IBM), E2
(Japan, Camellia predecessor), Serpent (Israel) are also
remain strong
 the most researched block cipher all over the world
(2014, open publications)
 basis for development of many other symmetric primitives

6. AES properties
 block length 128 bits only (subset of Rijndael which
supports 128, 192 and 256 bits)
 key length is 128, 192 and 256 bits
 uses Substitution-Permutation Network (SPN)
 number of rounds (10,12,14) depends on key length
 quite transparent design, algebraic structure
(theoretically may be vulnerable to algebraic
analysis)
 quite effective in software (32-bit platforms) and
hardware implementation

7. AES parameters: key length,
block size, number of rounds

8. AES: presentation of processing
bytes as a “cipher state”

9. AES: main steps
running key schedule procedure:
generation of all round keys
running encryption or decryption
procedure
 or, for compact hardware implementation,
sequential operations:
 generation of the current round key
 one encryption round

10. AES: high-level structure
(pseudocode)

11. AES: high-level structure
(picture for 128 bit key)

12. AES: SubBytes transformation

13. AES: ShiftRows
transformation

14. AES: MixColumns
transformation

15. AES: AddRoundKey
transformation

16. AES round key generation (key
expansion)
NB: not all key length (128, 192, 256) must be supported; for many
applications it’s enough to have the single key length

17. AES round key generation:
RotWord

18. AES round key generation:
SubBytes

19. AES round key generation:
round constant application
NB: without Rcon there would be equal blocks in ciphertext if plaintext and
keys have equal blocks (1, 2 or 4 bytes repeats in plaintext and key)

20. AES round key sequence

21. AES decryption (direct
presentation): reverse operations
in different order

22. AES/Rijndael design goals
 be extremely fast on 32 bit platforms (+++)
 be compact on hardware implementation with
small number of gates (++)
 possibility to implement cipher on 8-bit smart-
card processors actual for 1990th (++)
 cryptographic strength (+)

23. Direct implementation of AES
round function: SubBytes
16 operations (byte substitution)

24. Direct implementation of AES
round function: ShiftRows
12 operations (byte permutation)

25. AES: MixColumns
transformation
60 operations (logical and conditional):

3+ operations for each input byte (48+ total):
• shift and conditional XOR (mult by 02)
• XOR (mult by 03)

3 XORs for each row (12 total)

26. Direct implementation of AES
round function

SubBytes: 16 operations (byte substitution)

ShiftRows: 12 operations (byte permutation)

MixColumns: 60 or even more operations
(conditions will prevent effective pipelining)

AddRoundKey: 16 operations (logical)
TOTAL: more than 102 operations per round

27. AES effective software
implementation: 32-bit platform
 three different operations can be united
into the single (!) look-up table access:
 SubBytes (non-linear)
 ShiftRows (linear)
 MixColumns (linear)
 cipher consists of look-up table accesses and
round key additions

28. AES effective software
implementation: MixColumns
Matrix multiplication: 7 operations (4 memory look-ups + 3
XORs) instead of 60:

32-bit XOR of 4 columns

each column depends on one input byte only

all 4 bytes in each column are precomputed and stored in
advance

29. AES round function operations
sequence variants:
Original:

SubBytes

ShiftRows

MixColumns
Equivalent:

ShiftRows

SubBytes

MixColumns

30. AES effective software implementation:
MixColumns and SubBytes at one
precomputed table
SubBytes and MixColumns: 7 operations (4 memory look-ups + 3
XORs) total:

32-bit XOR of 4 columns

each column depends on one input byte only (already sent throw
S-box)

all 4 bytes in each column are precomputed and stored in advance

31. Fragment of OpenSSL AES source
code (based on Rijndael author's
implementation)
4 tables are needed; size of each table is 256 * 4 = 1 kByte

32. Fragment of OpenSSL AES source
code (based on Rijndael author's
implementation)
ShiftRows is implemented as usual shift and mask of 32-bit register;
SubBytes and MixColumns are implemented as memory lookups (8 bit → 32 bit)

33. AES effective software implementation:
extra memory optimization
Decreasing memory amount: single table (1 kByte instead of
4 tables of 1 kB each)

34. Main table size for the fastest and
compact optimized 32-bit AES
implementation
 fastest:
 (4 bytes) x (256 different entries to S-box) x
x (4 different positions for ShiftRow) == 4 kbytes
 compact optimized:
 (4 bytes) x (256 different entries to S-box) ==
== 1 kbyte
 three additional operations in C ( << , >>, | or ^)
are needed besides a table look-up
NB: for reaching highest performance precomputed tables and processing data
must fit into L1 processor cache (32-64kBytes for modern processors)

35. Number of 32-bit operations needed for a
single block encryption at main
transformation (having all round keys)
 ( (4 look-up) + (3 xors) ) * (4 columns) ==
== 28 operations / round
 4 xors with round keys ==
== 4 operations / round
 (28 + 4) * (9 rounds) == 288 operations for high
strength encryption of 9 rounds (!)
 (16 operations on SubBytes) + (24 operations on
ShiftRows) + (4 xors with round keys) ==
== 44 operations at last round

36. AES decryption: high-level
structure (pseudocode)

37. AES decryption: optimization
 SubBytes() and ShiftRows() transformations
commute, their sequence can be chaged
 The column mixing operations -
MixColumns() and InvMixColumns() – are
linear with respect to the column input, which
means InvMixColumns(state xor Round Key)
== InvMixColumns(state) xor
InvMixColumns(Round Key)

38. AES optimized decryption with
changed round keys

39. Additional details on AES
implementation
 two set of tables for encryption
 main optimized set (MixColumns, ShiftRows and
SubBytes)
 separate S-box array for the last round
 two set of tables for decryption (complexity is
the same as for encryption)
 main optimized set (InvMixColumns, InvShiftRows
and InvSubBytes)
 separate reverse S-box array for the last round
NB: ECB decryption is not needed for the most block cipher modes of operation

40. Conclusions
 direct AES implementation is very slow (requires
many byte operations and conditions)
 three different round function operations can be
united into the single look-up table access
 with effective implementation AES consists of look-
up table accesses and round key additions
 the fastest version AES requires 4 kB of memory for
tables, fast but compact requires 1 kB
 fast AES decryption operation has the same speed
as encryption and uses changed order of round
function operations with modified round keys