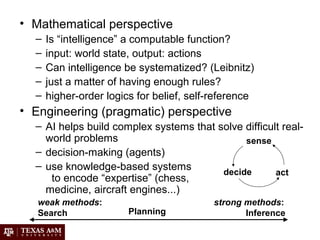
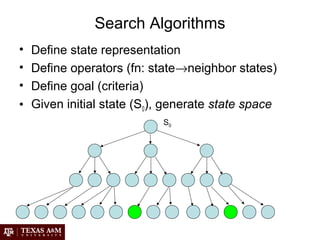
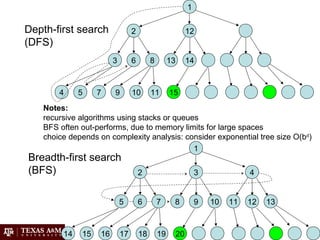
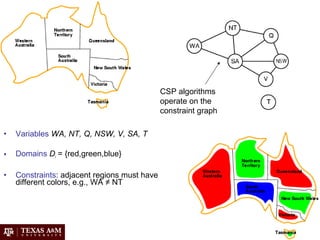
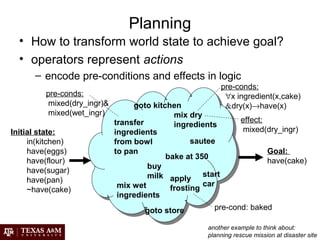
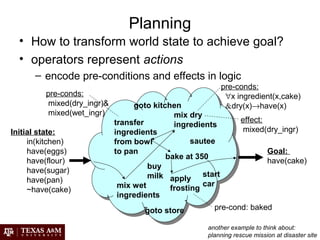
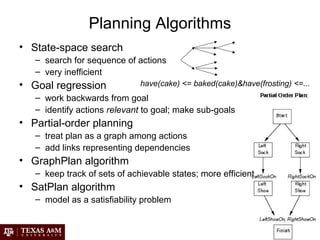
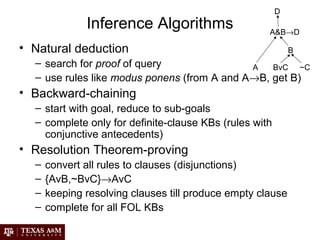
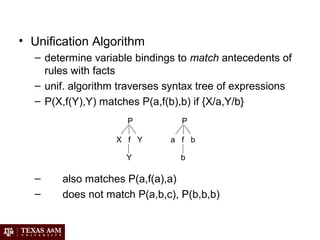
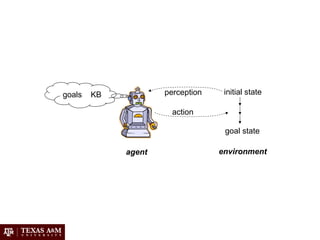
Artificial intelligence (AI) involves building intelligent agents that can perceive their environment and take actions to achieve goals. Different perspectives on AI include the philosophical question of what constitutes intelligence, the psychological perspective of human cognition, and the engineering approach of using AI to solve practical problems. Common techniques in AI include search algorithms, knowledge representation with logic, planning and problem solving with heuristics, and machine learning.

1. Overview of
Artificial Intelligence
Thomas R. Ioerger
Associate Professor
Department of Computer Science
Texas A&M University

2. What is AI?
• Real applications, not science fiction
– Control systems, diagnosis systems, games,
interactive animations, combat simulations,
manufacturing scheduling, transportation logistics,
financial analysis, computer-aided tutoring, search-
and-rescue robots

3. Different Perspectives
• Philosophical perspective
– What is the nature of “intelligence”? Can a
machine/program ever be truly “intelligent”?
– Strong AI hypothesis: Is acting intelligently sufficient?
– laws of thought; rational (ideal) decision-making
• Socrates is a man; men are mortal; therefore, Socrates is
mortal
• Psychological perspective
– What is the nature of “human intelligence”?
– Cognitive science – concept representations, internal
world model, information processing metaphor
– role of ST/LT memory? visualization? emotions?
analogy? creativity?
– build programs to simulate inference, learning...

4. • Mathematical perspective
– Is “intelligence” a computable function?
– input: world state, output: actions
– Can intelligence be systematized? (Leibnitz)
– just a matter of having enough rules?
– higher-order logics for belief, self-reference
• Engineering (pragmatic) perspective
– AI helps build complex systems that solve difficult real-
world problems
– decision-making (agents)
– use knowledge-based systems
to encode “expertise” (chess,
medicine, aircraft engines...)
sense
decide act
weak methods:
Search Planning
strong methods:
Inference

5. Search Algorithms
• Define state representation
• Define operators (fn: state→neighbor states)
• Define goal (criteria)
• Given initial state (S0), generate state space
S0

6. Many problems can be modeled as search
• tic-tac-toe
– states=boards, operator=moves
• symbolic integration
– states=equations, opers=algebraic manipulations
• class schedule
– states=partial schedule, opers=add/remove class
• rock band tour (traveling salesman problem)
– states=order of cities to visit, opers=swap order
• robot-motion planning
– states=robot configuration, opers=joint bending

7. 1
2 12
3 6 8 13 14
4 5 7 9 10 11 15
1
2 43
5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20
Depth-first search
(DFS)
Breadth-first search
(BFS)
Notes:
recursive algorithms using stacks or queues
BFS often out-performs, due to memory limits for large spaces
choice depends on complexity analysis: consider exponential tree size O(bd
)

8. Heuristics
• give guidance to search in terms of which nodes
look “closest to the goal”
– node evaluation function
– h(n)=w1*(piece_differential)+w2*(center_control)+
w3*(#pieces_can_be_taken)+w4*(#kings)
• greedy algorithms search these nodes first
• bias direction of search to explore “best” parts of
state space (most likely to contain goal)
• A* algorithm
– optimal (under certain conditions)
– finds shortest path to a goal
– insensitive to errors in heuristic function

9. Specialized Search Algorithms
• Game-playing
– two-player zero-sum games (alternate moves)
– minimax algorithm: form of “look-ahead” – If I make a
move, how will opponent likely respond? Which move
leads to highest assured payoff?
• Constraint-satisfaction problems (CSPs)
– state=partial variable assignment
– goal find assignment that satisfies constraints
– algorithms use back-tracking, constraint propagation,
and heuristics
– pre-process constraint-graph to make more efficient
– examples: map-coloring, propositional satisfiability,
server configuration

10. • Variables WA, NT, Q, NSW, V, SA, T
• Domains Di = {red,green,blue}
• Constraints: adjacent regions must have
different colors, e.g., WA ≠ NT
CSP algorithms
operate on the
constraint graph

11. Planning
• How to transform world state to achieve goal?
• operators represent actions
– encode pre-conditions and effects in logic
Initial state:
in(kitchen)
have(eggs)
have(flour)
have(sugar)
have(pan)
~have(cake)
Goal:
have(cake)
mix dry
ingredients
mix wet
ingredients
transfer
ingredients
from bowl
to pan
bake at 350
apply
frosting
pre-conds:
∀x ingredient(x,cake)
&dry(x)→have(x)
effect:
mixed(dry_ingr)
pre-conds:
mixed(dry_ingr)&
mixed(wet_ingr)
pre-cond: baked
goto kitchen
goto store
start
car
buy
milk
sautee
another example to think about:
planning rescue mission at disaster site

12. Planning
• How to transform world state to achieve goal?
• operators represent actions
– encode pre-conditions and effects in logic
Initial state:
in(kitchen)
have(eggs)
have(flour)
have(sugar)
have(pan)
~have(cake)
Goal:
have(cake)
mix dry
ingredients
mix wet
ingredients
transfer
ingredients
from bowl
to pan
bake at 350
apply
frosting
pre-conds:
∀x ingredient(x,cake)
&dry(x)→have(x)
effect:
mixed(dry_ingr)
pre-conds:
mixed(dry_ingr)&
mixed(wet_ingr)
pre-cond: baked
goto kitchen
goto store
start
car
buy
milk
sautee
another example to think about:
planning rescue mission at disaster site

13. Planning Algorithms
have(cake) <= baked(cake)&have(frosting) <=...
• State-space search
– search for sequence of actions
– very inefficient
• Goal regression
– work backwards from goal
– identify actions relevant to goal; make sub-goals
• Partial-order planning
– treat plan as a graph among actions
– add links representing dependencies
• GraphPlan algorithm
– keep track of sets of achievable states; more efficient
• SatPlan algorithm
– model as a satisfiability problem

14. Knowledge-Based Methods
• need: representation for search heuristics and planning
operators
• need expertise to produce expert problem-solving behavior
• first-order logic – a formal language for representing
knowledge
• rules, constraints, facts, associations, strategies...
– rain(today)→wet(road)
– fever→infection
– in(class_C_air_space)→reduce(air_speed,150kts)
– can(take_opp_queen,X)&~losing_move(X)→do(X)
• use knowledge base (KB) to infer what to do
– goals & initial_state & KB do(action)
– need inference algorithms to derive what is entailed
• declarative vs. procedural programming

15. First-Order Logic
• lingua franca of AI
• syntax
– predicates (relations): author(Candide,Voltaire)
– connectives: & (and), v (or), ~ (not), → (implies)
– quantified variables: ∀X person(X)→∃Y mother(X,Y)
• Ontologies – systems of concepts for writing KBs
– categories of stuff (solids, fluids, living, mammals, food,
equipment...) and their properties
– places (in), part_of, measures (volume)
– domain-dependent: authorship, ambush, infection...
– time, action, processes (Situation Calculus, Event Logic)
– beliefs, commitments
• issues: granularity, consistency, expressiveness

16. Inference Algorithms
• Natural deduction
– search for proof of query
– use rules like modus ponens (from A and A→B, get B)
• Backward-chaining
– start with goal, reduce to sub-goals
– complete only for definite-clause KBs (rules with
conjunctive antecedents)
• Resolution Theorem-proving
– convert all rules to clauses (disjunctions)
– {AvB,~BvC}→AvC
– keeping resolving clauses till produce empty clause
– complete for all FOL KBs
D
A&B→D
A BvC ~C
B

17. Prolog and Expert Systems
• Automated deduction systems
• programming = writing rules
• make query, system responds with true/false
plus variable bindings
• inference algorithm based on backward-chaining

18. Prolog example
sibling(X,Y) :- parent(Z,X), parent(Z,Y).
grandfather(X,Y) :- father(X,Z),parent(Z,Y).
parent(X,Y) :- father(X,Y).
parent(X,Y) :- mother(X,Y).
mother(tracy, sally).
father(bill, sally).
father(bill, erica).
father(mike, bill).
?- sibling(sally,erica).
Yes
?- grandfather(sally,X).
grandfather(sally,mike)

19. • Unification Algorithm
– determine variable bindings to match antecedents of
rules with facts
– unif. algorithm traverses syntax tree of expressions
– P(X,f(Y),Y) matches P(a,f(b),b) if {X/a,Y/b}
– also matches P(a,f(a),a)
– does not match P(a,b,c), P(b,b,b)
P
X f Y
Y
P
a f b
b

20. • Managing Uncertainty in real expert systems
– default/non-monotonic logics (assumptions)
– certainty factors (degrees of beliefs)
– probabilistic logics
– Bayesian networks (causal influences)
• Complexity of inference?
– suitable for real-time applications?

21. Application of Data Structures and
Algorithms in AI
• priority queues in search algorithms
• recursion in search algorithms
• shortest-path algorithm for planning/robotics
• hash tables for indexing rules by predicate in KBS
• dynamic programming to improve efficiency of
theorem-provers (caching intermediate inferences)
• graph algorithms for constraint-satisfaction
problems (arc-consistency)
• complexity analysis to select search algorithm
based on branching factor and depth of solution for
a given problem

22. Use of AI in Research
• intelligent agents for flight simulation
– collaboration with Dr. John Valasek (Aerospace Eng.)
– goal: on-board decision-making without ATC
– approach: use 1) multi-agent negotiation, 2)
reinforcement learning
• pattern recognition in protein crystallography
– collaboration with Dr. James Sacchettini (Biochem.)
– goal: automate determination of protein structures
from electron density maps
– approach: extract features representing local 3D
patterns of electron density and use to recognize
amino acids and build
– uses neural nets, and heuristics encoding knowledge
of typical protein conformations and contacts

23. • TAMU courses on AI
– CPSC 420/625 – Artificial Intelligence
– undergrad
• CPSC 452 – Robotics and Spatial Intelligence
• also related: CPSC 436 (HCI) and CPSC 470 (IR)
– graduate
• CPSC 609 - AI Approaches to Software Engineering*
• CPSC 631 – Agents/Programming Environments for AI
• CPSC 632 - Expert Systems*
• CPSC 633 - Machine Learning
• CPSC 634 Intelligent User Interfaces
• CPSC 636 - Neural Networks
• CPSC 639 - Fuzzy Logic and Intelligent Systems
• CPSC 643 Seminar in Intelligent Systems and Robotics
• CPSC 644 - Cortical Networks
• CPSC 666 – Statistical Pattern Recognition (not official yet)
• Special Topics courses (CPSC 689)...
• * = not actively taught

24. goals KB initial state
goal state
perception
action
agent environment