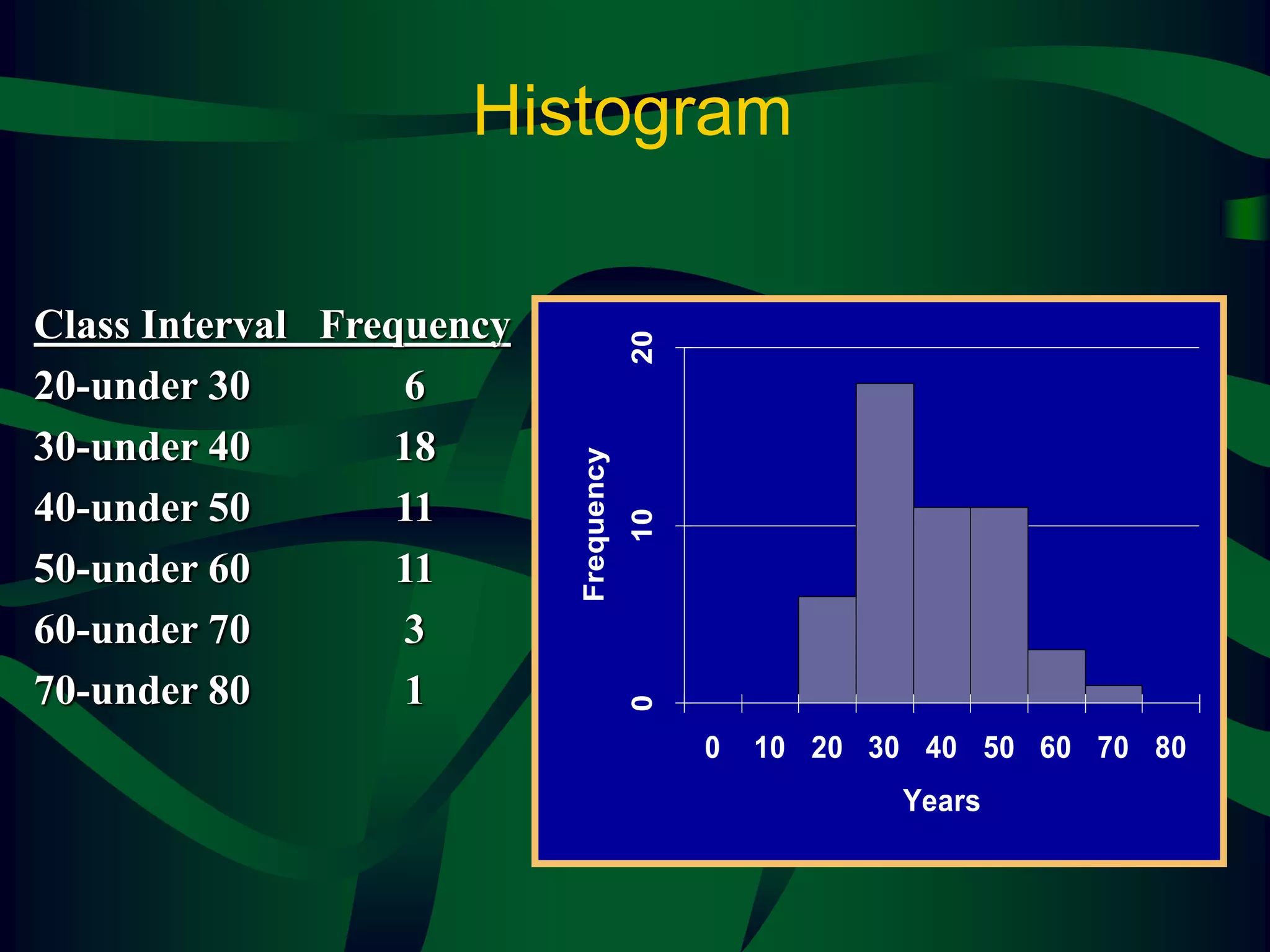
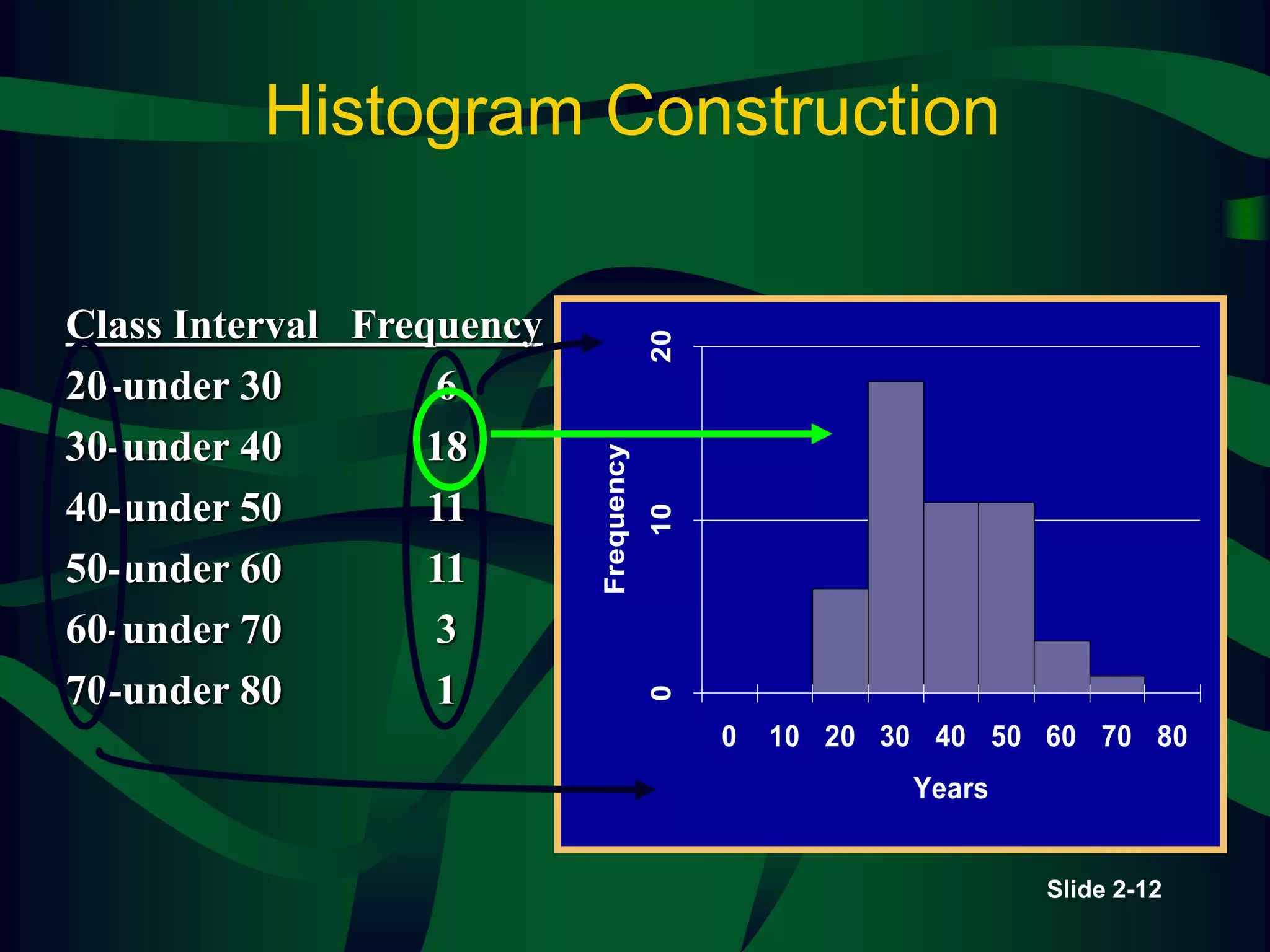
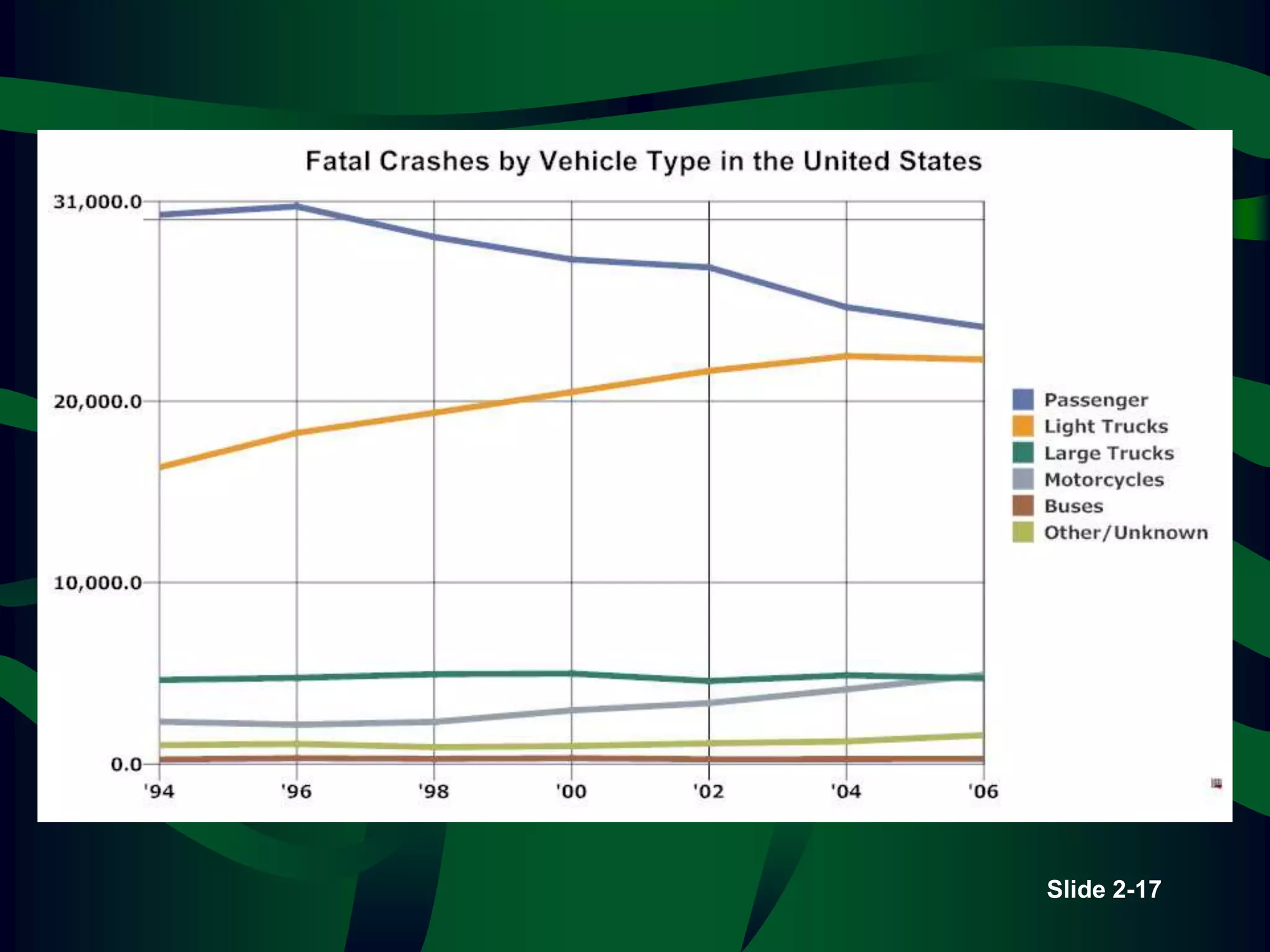
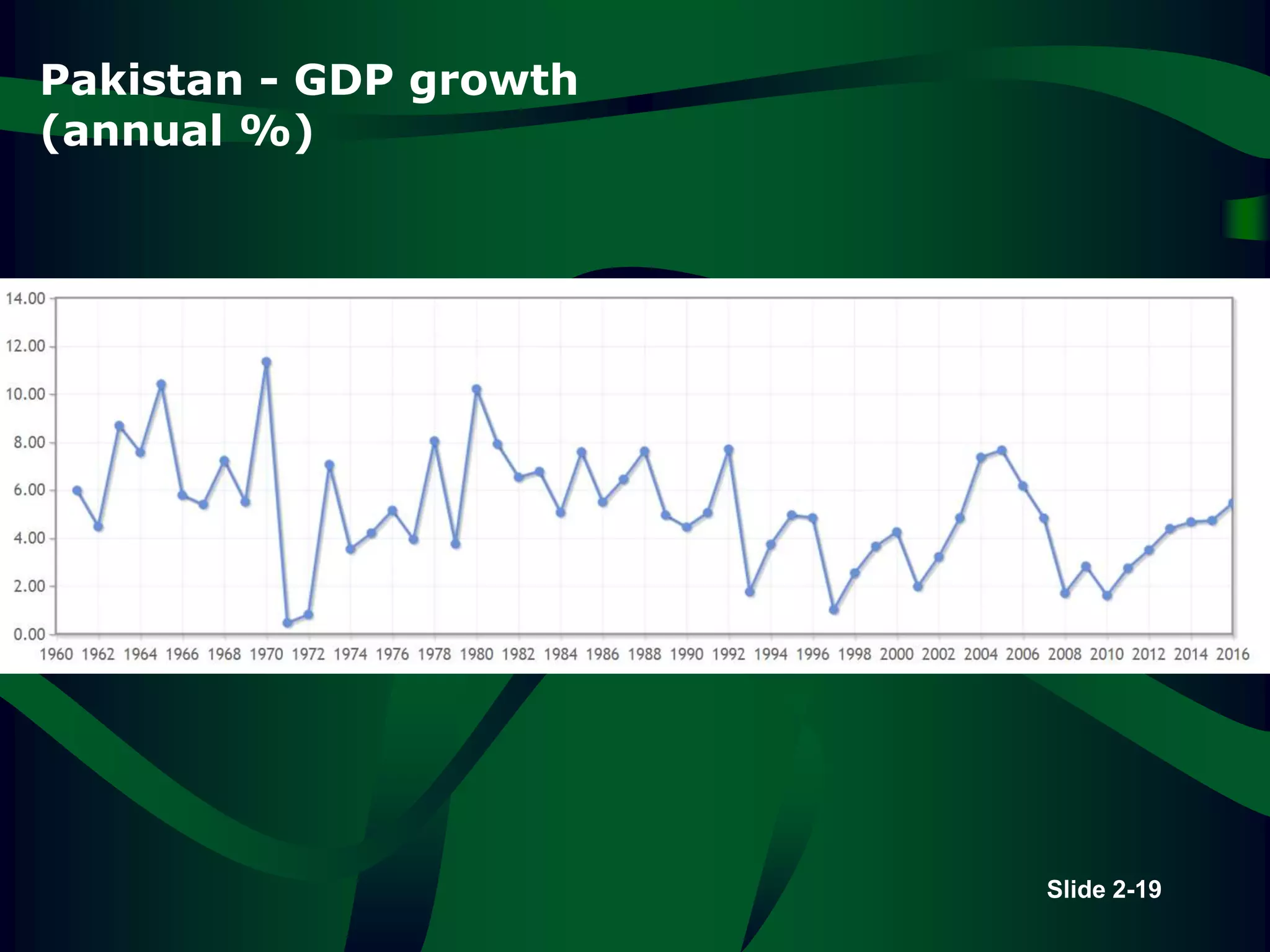
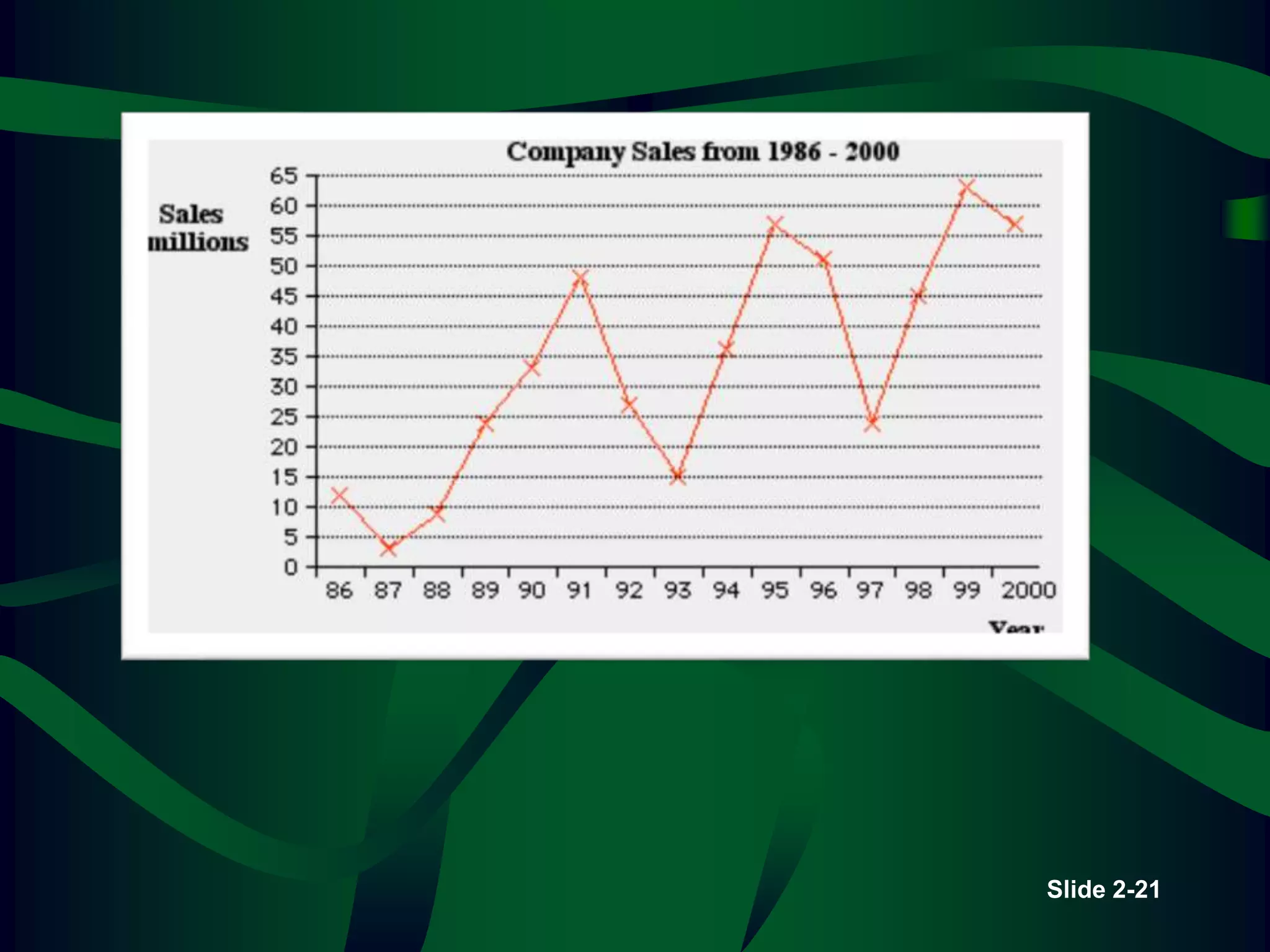
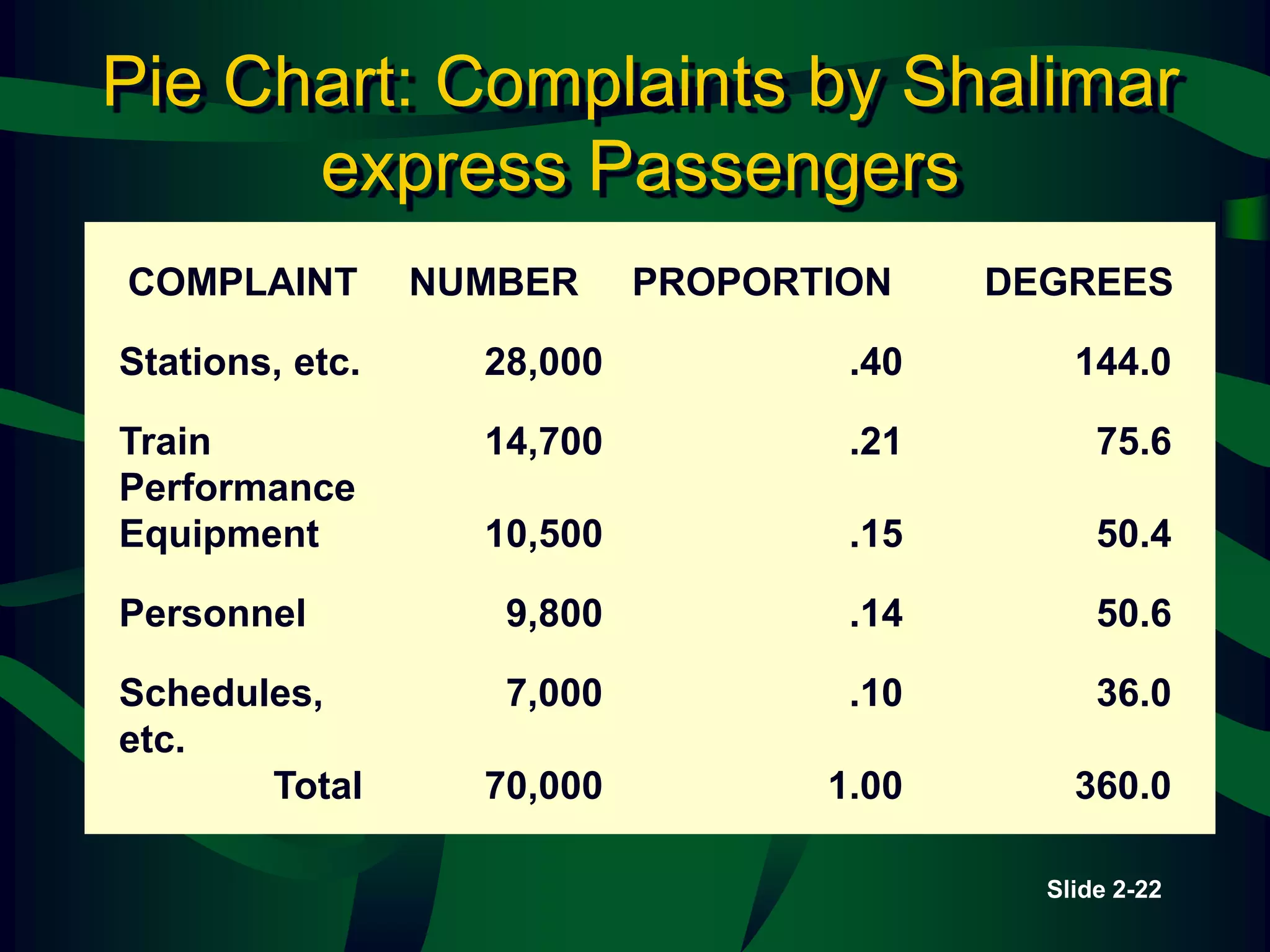
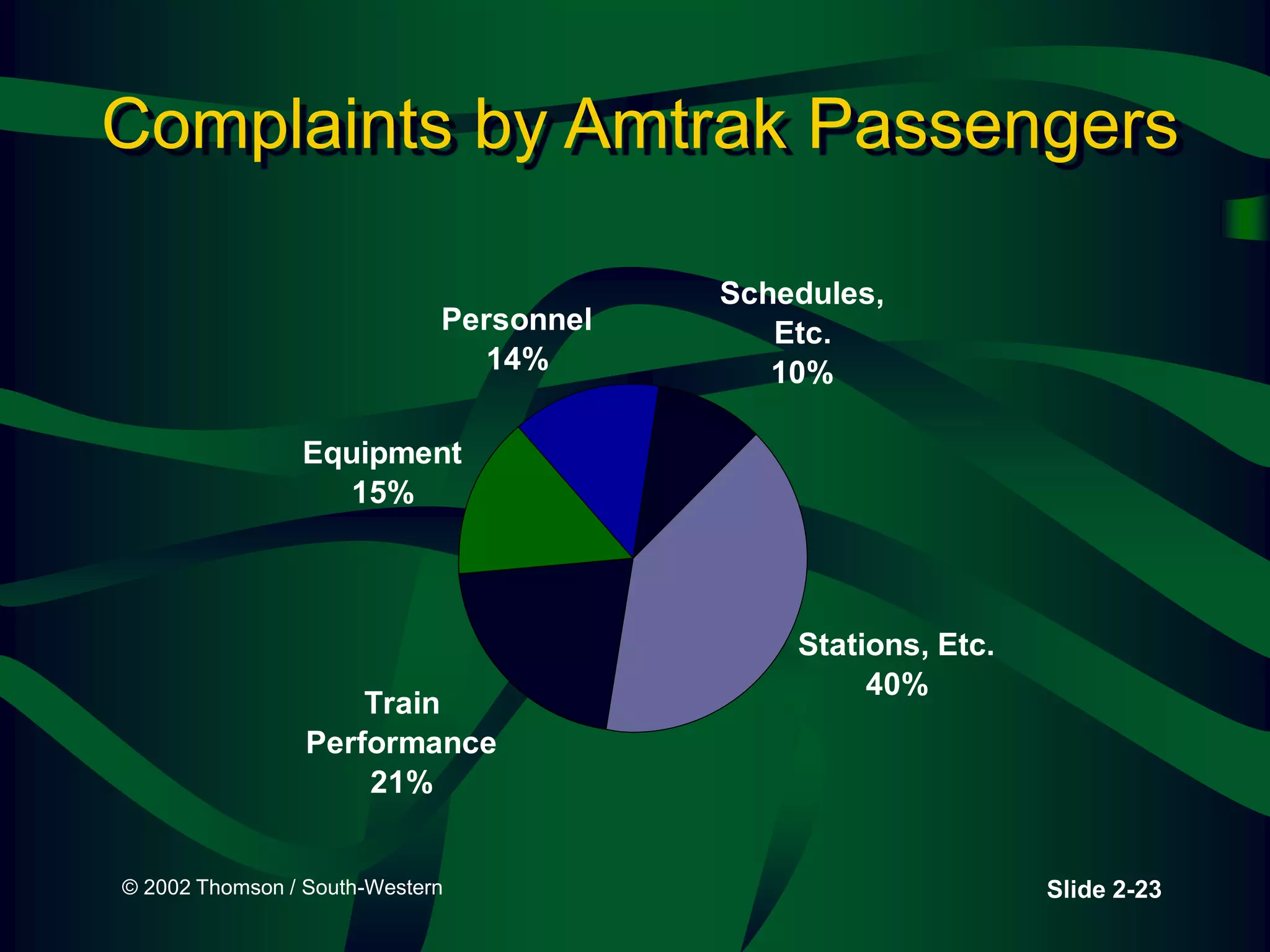
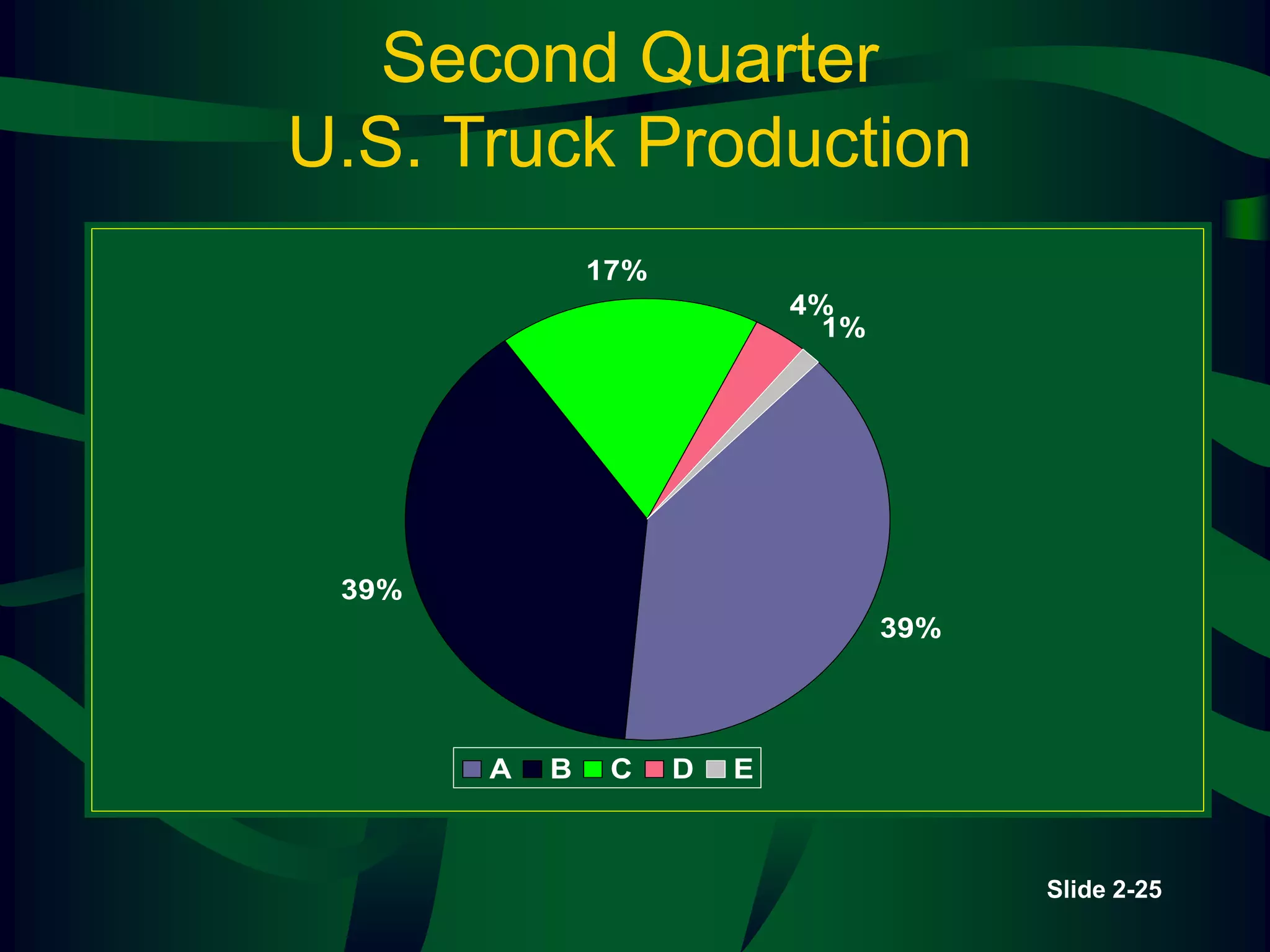
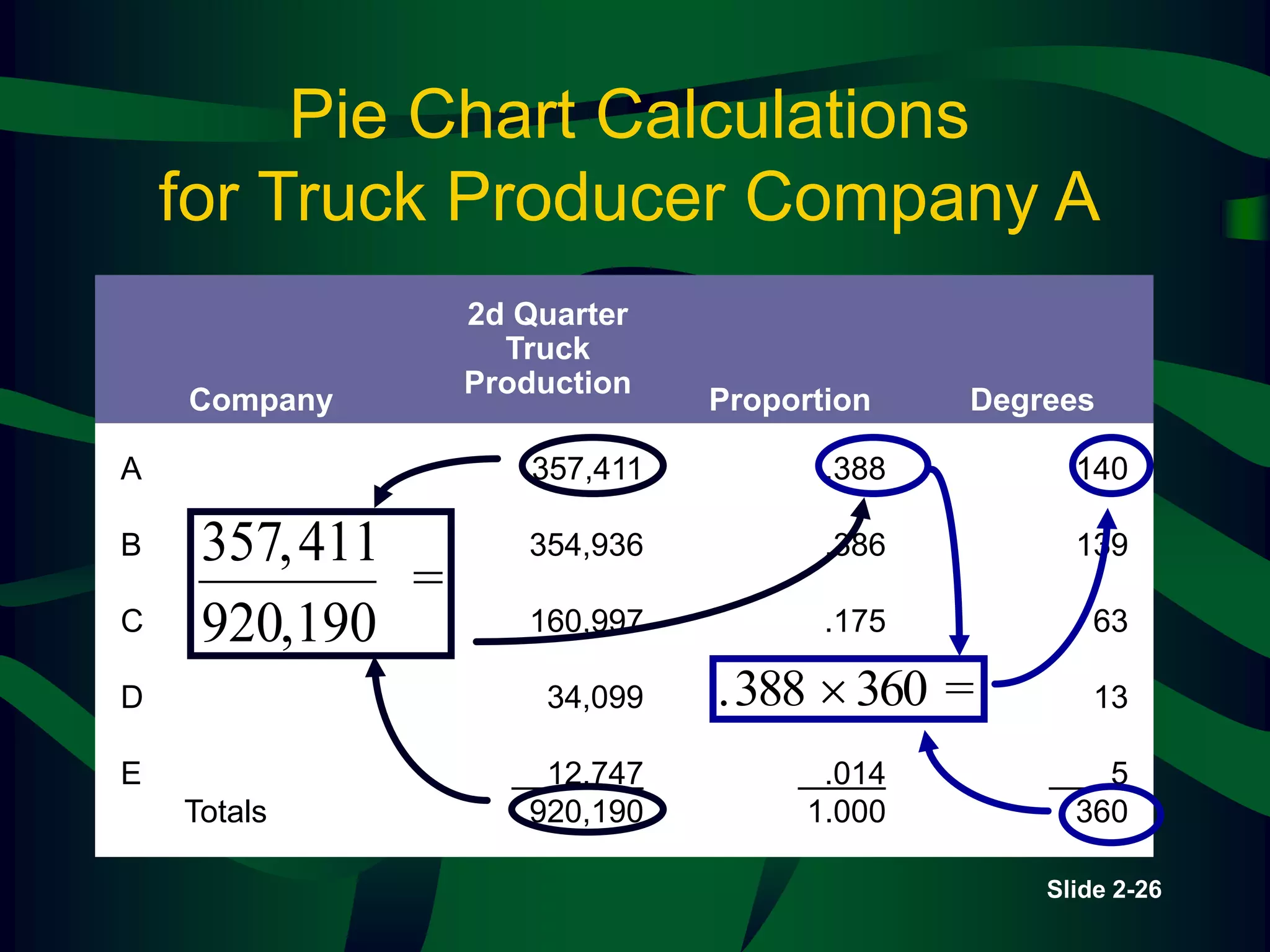
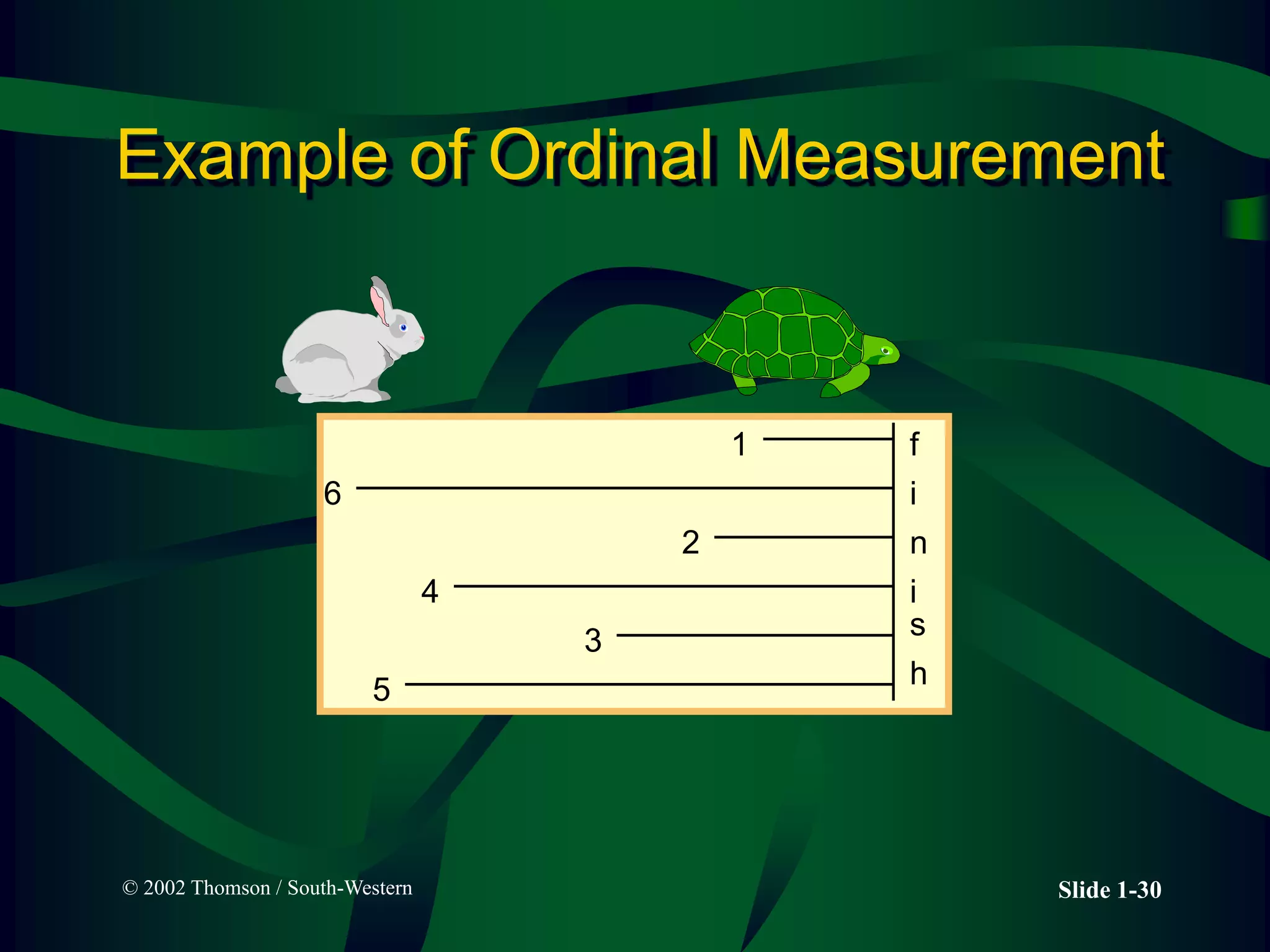
The lecture covers descriptive statistics, differentiating between ungrouped (raw) and grouped data, with examples of age distributions of child care managers in the U.S. It explains histogram construction, cumulative frequencies, relative frequencies, and various types of statistical graphs like line and pie charts. Additionally, it discusses levels of data measurement (nominal, ordinal, interval, ratio) and the classification of qualitative versus quantitative data.

1. Business statistics
LECTURE 3
Descriptive Charts and
Graphs
Instructor: Araiz Murad Dahir.

2. Slide 2-2
Ungrouped vs Grouped Data
• Ungrouped data
• have not been summarized in any
way
• are also called raw data
• Grouped data
• have been organized into a
frequency distribution

3. Slide 2-3
Example of Ungrouped Data
42
30
53
50
52
30
55
49
61
74
26
58
40
40
28
36
30
33
31
37
32
37
30
32
23
32
58
43
30
29
34
50
47
31
35
26
64
46
40
43
57
30
49
40
25
50
52
32
60
54
Ages of a Sample
of Managers
from Urban
Child Care
Centers in the
United States

4. Slide 2-4
Frequency Distribution
of Child Care Manager’s Ages
Class Interval Frequency
20-under 30 6
30-under 40 18
40-under 50 11
50-under 60 11
60-under 70 3
70-under 80 1

5. Slide 2-5
Data Range
42
30
53
50
52
30
55
49
61
74
26
58
40
40
28
36
30
33
31
37
32
37
30
32
23
32
58
43
30
29
34
50
47
31
35
26
64
46
40
43
57
30
49
40
25
50
52
32
60
54
Smallest
Largest
Range = Largest - Smallest
= 74 - 23
= 51

6. Slide 2-6
Relative Frequency
Relative
Class Interval Frequency Frequency
20-under 30 6 .12
30-under 40 18 .36
40-under 50 11 .22
50-under 60 11 .22
60-under 70 3 .06
70-under 80 1 .02
Total 50 1.00
6
50

18
50


7. Slide 2-7
Cumulative Frequency
Cumulative
Class Interval Frequency CF
20-under 30 6 6
30-under 40 18 24
40-under 50 11 35
50-under 60 11 46
60-under 70 3 49
70-under 80 1 50
Total 50
18 + 6
11 + 24

8. Slide 2-8
Relative Frequencies, and Cumulative
Frequencies
Relative Cumulative
Class IntervalFrequency Frequency Frequency
20-under 30 6 .12 6
30-under 40 18 .36 24
40-under 50 11 .22 35
50-under 60 11 .22 46
60-under 70 3 .06 49
70-under 80 1 .02 50
Total 50 1.00

9. Slide 2-9
Cumulative Relative Frequencies
Cumulative
Relative Cumulative Relative
Class Interval Frequency Frequency Frequency Frequency
20-under 30 6 .12 6 .12
30-under 40 18 .36 24 .48
40-under 50 11 .22 35 .70
50-under 60 11 .22 46 .92
60-under 70 3 .06 49 .98
70-under 80 1 .02 50 1.00
Total 50 1.00

10. Common Statistical Graphs
• Histogram -- vertical bar chart of
frequencies
• Line Graph.
• Time Series Graph.
• Pie Chart -- proportional representation
for categories of a whole

11. Histogram
Class Interval Frequency
20-under 30 6
30-under 40 18
40-under 50 11
50-under 60 11
60-under 70 3
70-under 80 1
0
10
20
0 10 20 30 40 50 60 70 80
Years
Frequency

12. Slide 2-12
Histogram Construction
Class Interval Frequency
20-under 30 6
30-under 40 18
40-under 50 11
50-under 60 11
60-under 70 3
70-under 80 1
0
10
20
0 10 20 30 40 50 60 70 80
Years
Frequency

13. QUESTION
• Make Histogram of SUSPECTED
NUCLEAR WEAPONS.
• 1. USA 15500
• 2. RUSSIA 15000
• 3. FRANCE 482
• 4. CHINA 410
• 5. UK 200
• 6. ISRAEL 100
Slide 2-13

14. Suspected Nuclear Weapons
15500
15000
482 410 200 100 60 20
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
U
n
i
t
e
d
S
t
a
t
e
s
R
u
s
s
i
a
F
r
a
n
c
e
C
h
i
n
a
U
n
i
t
e
d
K
i
n
g
d
o
m
I
s
r
a
e
l
I
n
d
i
a
P
a
k
i
s
t
a
n
Source: Center for Defense Information

15. Slide 2-15
Line Graph
- A line graph, also known as a line chart, is a
type of chart used to visualize the value of
something over time.
- For example, a finance department may plot the
change in the amount of cash the company has
on hand over time.
- Data points are plotted and connected by a line in a
"dot-to-dot" fashion.

16. Slide 2-16
- More than one line may be plotted in the same axis as a form
of comparison.
- For example, you could create a line graph comparing Fatal
accidents by vehicle types. In this case each line would have
a different color, identified in a legend.
Line Graph

17. Slide 2-17

18. Slide 2-18
- A time series graph is a line graph of repeated measurements
taken over regular time intervals.
- Time is always shown on the horizontal axis.
- On time series graphs data points are drawn at regular
intervals and the points joined, usually with straight lines.
- Time series graphs help to show trends or patterns.
Line Graph type:
Time series graph

19. Slide 2-19
Pakistan - GDP growth
(annual %)

20. Slide 2-20

21. Slide 2-21

22. Slide 2-22
Pie Chart: Complaints by Shalimar
express Passengers
COMPLAINT NUMBER PROPORTION DEGREES
Stations, etc. 28,000 .40 144.0
Train
Performance
14,700 .21 75.6
Equipment 10,500 .15 50.4
Personnel 9,800 .14 50.6
Schedules,
etc.
7,000 .10 36.0
Total 70,000 1.00 360.0

23. © 2002 Thomson / South-Western Slide 2-23
Complaints by Amtrak Passengers
Stations, Etc.
40%
Train
Performance
21%
Equipment
15%
Personnel
14%
Schedules,
Etc.
10%

24. Slide 2-24
Second
Quarter Truck
Production in
the U.S.
(Hypothetical
values)
2d Quarter
Truck
Production
Company
A
B
C
D
E
Totals
357,411
354,936
160,997
34,099
12,747
920,190

25. Slide 2-25
39%
39%
17%
4%
1%
A B C D E
Second Quarter
U.S. Truck Production

26. Slide 2-26
Pie Chart Calculations
for Truck Producer Company A
2d Quarter
Truck
Production
Proportion Degrees
Company
A
B
C
D
E
Totals
357,411
354,936
160,997
34,099
12,747
920,190
.388
.386
.175
.037
.014
1.000
140
139
63
13
5
360
357,411
920,190
=
.388 360 =


27. Slide 1-27
Levels of Data Measurement
• Nominal - Lowest level of measurement
• Ordinal
• Interval
• Ratio - Highest level of measurement

28. Slide 1-28
Nominal Level Data
• Numbers are used to classify or
categorize
Example: Employment Classification
– 1 for Educator
– 2 for Construction Worker
– 3 for Manufacturing Worker
Example: Ethnicity
– 1 for African-American
– 2 for Anglo-American
– 3 for Hispanic-American
– 4 for Oriental-American

29. Slide 1-29
Ordinal Level Data
• Numbers are used to indicate rank or order
– Relative magnitude of numbers is meaningful
– Differences between numbers are not comparable
Example: Taste test ranking of three brands of soft
drink
Example: Position within an organization
– 1 for President
– 2 for Vice President
– 3 for Plant Manager
– 4 for Department Supervisor
– 5 for Employee

30. © 2002 Thomson / South-Western Slide 1-30
Example of Ordinal Measurement
f
i
n
i
s
h
1
2
3
4
5
6

31. © 2002 Thomson / South-Western Slide 1-31
Ordinal Data
Faculty and staff should receive preferential
treatment for parking space.
1 2 3 4 5
Strongly
Agree
Agree Strongly
Disagree
Disagree
Neutral

32. © 2002 Thomson / South-Western Slide 1-32
Interval Level Data
• Distances between consecutive integers
are equal
– Relative magnitude of numbers is
meaningful
– Differences between numbers are
comparable
– Location of origin, zero, is arbitrary
Examples: Fahrenheit Temperature, Calendar
Time, Monetary Units

33. © 2002 Thomson / South-Western Slide 1-33
Ratio Level Data
• Highest level of measurement
– Relative magnitude of numbers is meaningful
– Differences between numbers are
comparable
Examples: Height, Weight, and Volume
Monetary Variables, such as Revenues, and
Expenses
Financial ratios, such as P/E Ratio, Inventory
Turnover

34. © 2002 Thomson / South-Western Slide 1-34
Usage Potential of Various
Levels of Data
Nominal
Ordinal
Interval
Ratio

35. © 2002 Thomson / South-Western Slide 1-35
Qualitative vs Quantitative Data
Qualitative Data is data of the nominal or
ordinal level that classifies by a label or
category. The labels may be numeric or
nonnumeric.
Quantitative Data is data of the interval or
ratio level that measures on a naturally
occurring numeric scale.

36. © 2002 Thomson / South-Western Slide 1-36
Discrete and Continuous Data
Discrete Data is numeric data in which the
values can come only from a list of specific
values. Discrete data results from a counting
process.
Continuos Data is numeric data that can take
on values at every point over a given interval.
Continuous data result from a measuring
process.

37. © 2002 Thomson / South-Western Slide 1-37
Summary of Data Classifications
Data
nal Ordinal
Interl
Ratio
Qualitative
(Categorical)
Quantitative
Nonnumeric Numeric
Discrete
Numeric
Discrete or
Continuous
Data
Nominal Ordinal Interval Ratio
Quantitative
Qualitative
Numeric Numeric
Discrete
Nonnumeric
Discrete or
Continuous