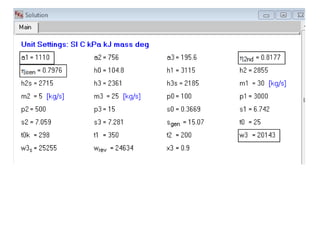
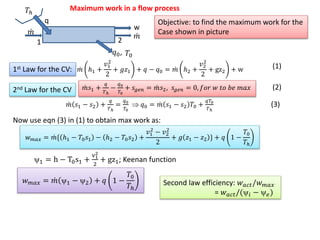
The maximum work that can be obtained from a system initially at a higher temperature T than the environment at T0 is equal to the initial available energy minus the available energy at the final state. For an irreversible process, the actual work is always less than the maximum reversible work, with the difference equal to T0 times the entropy generation. The maximum work from a flow process is equal to the change in availability plus any heat input times 1 minus the ratio of environment to heat source temperatures.

1. Maximum work or available energy from a system
Initially a body of mass m, is at temp T, what is the maximum work that
can be obtained out of it if the environment is at 𝑇0 which is lower than
the body temperature T.
𝑇0
𝑄ℎ
𝑄𝑙
w
𝑚𝑐 𝑣 𝑇
𝑄ℎ = 𝑚𝑐 𝑣 𝑇 − 𝑇0 ; ∆𝑠 𝑏 = 𝑚𝑐 𝑣 ln
𝑇0
𝑇
∆𝑠𝑠𝑢𝑟 = 𝑄𝑙/𝑇0 For max work output, ∆𝑠𝑠𝑢𝑟 + ∆𝑠 𝑏 = 0
𝑄𝑙 = −𝑇0 𝑚 𝑐 𝑣 ln
𝑇0
𝑇
;
𝑤 = 𝑄ℎ − 𝑄𝑙 = 𝑚𝑐 𝑣 𝑇 − 𝑇0 − 𝑇0 𝑚𝑐 𝑣 ln
𝑇
𝑇0
𝑤 = 𝑚𝑐 𝑣 𝑇 − 𝑇0 − 𝑇0 ln
𝑇
𝑇0
= 𝑈1 − 𝑈0 − 𝑇0(𝑆1 − 𝑆0)
= 𝑈1 − 𝑇0 𝑆1 − 𝑈0 − 𝑇0 𝑆0
= 𝐹1 − 𝐹0; 𝑤ℎ𝑒𝑟𝑒 𝐹 = 𝑈 − 𝑇0 𝑆, 𝐹 𝑖𝑠 𝑐𝑎𝑙𝑙𝑒𝑑 𝑡ℎ𝑒 𝑎𝑣𝑎𝑖𝑙𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑟 𝐻𝑒𝑙𝑚𝑜𝑙𝑡𝑧 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛
If the system boundary expands against the atmospheric pressure p0 then F becomes:
𝜑 = 𝑈 − 𝑇0 𝑆 + 𝑝0 𝑉, 𝜑1 − 𝜑2 = 𝑎𝑣𝑎𝑖𝑙𝑎𝑏𝑙𝑒 𝑤𝑜𝑟𝑘 = 𝑤 𝑚𝑎𝑥

2. cm
𝑇0
𝑄12
𝑄0
w12
𝑇ℎ
Control mass process when the system receives heat from a source
Maximum work or available energy
𝑈1 − 𝑈2
𝑆1 − 𝑆2
The system goes from 1-2, does work w12 and rejects heat 𝑄0
Lets us consider two situations: the body rejects heat either
reversibly or irreversibly, but it receives heat reversibly.
𝑄12 − 𝑄0
𝑖𝑟𝑟
= 𝑈2 − 𝑈1 + 𝑤12
𝑎𝑐𝑡
𝑠 𝑔𝑒𝑛 = ∆𝑠𝑐𝑚 + ∆𝑠𝑠𝑢𝑟 + ∆𝑠𝑟𝑒𝑠 > 0, for irrev process
𝑠𝑔𝑒𝑛
𝑟𝑒𝑣
= 𝑆2 − 𝑆1 +
𝑄0 𝑟𝑒𝑣
𝑇0
−
𝑄12
𝑇ℎ
= 0 for rev process
𝑄0
𝑟𝑒𝑣
= −𝑇0 𝑆2 − 𝑆1 +
𝑇0
𝑇ℎ
Q12,
From 1st law for the CM we get:
𝑄12 − 𝑄0
𝑟𝑒𝑣
= 𝑤12
𝑟𝑒𝑣
+ 𝑈2 − 𝑈1
𝑤12
𝑟𝑒𝑣
= 𝑄12 − 𝑄0
𝑟𝑒𝑣
− 𝑈2 − 𝑈1
𝑤12
𝑟𝑒𝑣
= 𝑄12 + 𝑇0 𝑆2 − 𝑆1 −
𝑄12 𝑇0
𝑇ℎ
− 𝑈2 − 𝑈1
𝑤12
𝑟𝑒𝑣
= 𝑄12 1 −
𝑇0
𝑇ℎ
+ 𝑈1 − 𝑇0 𝑆1 − 𝑈2 − 𝑇0 𝑆2
𝑤12
𝑟𝑒𝑣
= 𝑤 𝑚𝑎𝑥 = 𝑄12 1 −
𝑇0
𝑇ℎ
+ 𝐹1 − 𝐹2
sur
res
𝑤12
𝑎𝑐𝑡
= 𝑄12 − 𝑄0
𝑖𝑟𝑟
− 𝑈2 − 𝑈1
𝐼 = 𝐼𝑟𝑟 = 𝑤12
𝑟𝑒𝑣
− 𝑤12
𝑎𝑐𝑡
= 𝑇0 𝑆2 − 𝑆1 −
𝑄12 𝑇0
𝑇ℎ
+ 𝑄0
𝑖𝑟𝑟
= 𝑇0 𝑆2 − 𝑆1 −
𝑄12
𝑇ℎ
+
𝑄0
𝑖𝑟𝑟
𝑇0
= 𝑇0(∆𝑠𝑐𝑚 + ∆𝑠𝑟𝑒𝑠 + ∆𝑠𝑠𝑢𝑟)
= 𝑇0∆𝑠 𝑢𝑛𝑖𝑣 = 𝑇0 𝑠𝑔𝑒𝑛
Measure of irreversibility

3. NH3
100C
Example problem: 1kg of NH3 is contained in a spring loaded piston/cylinder
as saturated liquid at -20C. Heat is added from a reservoir
at 100C until a final state of 800kpa, 70C is reached. Find
the work, heat transfer, and entropy generation assuming
the process to be internally reversible.
p1=pressure(r717,t=-20,x=0)
v1=volume(r717,t=-20,x=0)
u1=intenergy(r717,t=-20,x=0)
s1=entropy(r717,t=-20,x=0)
v2=volume(r717,p=800,t=70)
u2=intenergy(r717,t=70,p=800)
s2=entropy(r717,t=70,p=800)
w12=(800+p1)*.5*(v2-v1)
q12=w12+u2-u1
s_gen+q12/373=s2-s1

4. Maximum work in a flow process
1 2
w
𝑚
𝑚
q
𝑇ℎ
𝑇0𝑞0,
Objective: to find the maximum work for the
Case shown in picture
1st Law for the CV: 𝑚 ℎ1 +
𝑣1
2
2
+ 𝑔𝑧1 + 𝑞 − 𝑞0 = 𝑚 ℎ2 +
𝑣2
2
2
+ gz2 + w
𝑚𝑠1 +
𝑞
𝑇ℎ
−
𝑞0
𝑇0
+ 𝑠𝑔𝑒𝑛 = 𝑚𝑠2, 𝑠𝑔𝑒𝑛 = 0, 𝑓𝑜𝑟 𝑤 𝑡𝑜 𝑏𝑒 𝑚𝑎𝑥2nd Law for the CV
𝑚 𝑠1 − 𝑠2 +
𝑞
𝑇ℎ
=
𝑞0
𝑇0
 𝑞0 = 𝑚 𝑠1 − 𝑠2 𝑇0 +
𝑞𝑇0
𝑇ℎ
(1)
(2)
Now use eqn (3) in (1) to obtain max work as:
(3)
𝑤 𝑚𝑎𝑥 = 𝑚{ ℎ1 − 𝑇0 𝑠1 − ℎ2 − 𝑇0 𝑠2 +
𝑣1
2
− 𝑣2
2
2
+ 𝑔 𝑧1 − 𝑧2 } + 𝑞 1 −
𝑇0
𝑇ℎ
1 = h − T0s1 +
v1
2
2
+ gz1; Keenan function
𝑤 𝑚𝑎𝑥 = 𝑚 1 − 2 + 𝑞 1 −
𝑇0
𝑇ℎ
Second law efficiency: 𝑤 𝑎𝑐𝑡/𝑤 𝑚𝑎𝑥
= 𝑤 𝑎𝑐𝑡/(𝑖 −  𝑒)

5. T
S
1
2
2s
P=p1
P=p2
(ℎ1−ℎ2)/(ℎ1 − ℎ2𝑠) = _𝑖𝑠𝑒𝑛, 𝑡𝑢𝑟
For the case of a turbine expansion
P=p2
1
2s
2
T
S
P=p1
For the case of a compressor
(ℎ1−ℎ2𝑠)/(ℎ1 − ℎ2) = _𝑖𝑠𝑒𝑛, 𝑐𝑜𝑚𝑝
An insulated steam turbine, receives 30kg/s of steam at 3 Mpa, 350C . In the
turbine where the pressure is 500kpa, steam is beld off at the rate of 5kg/s, for
processing equipment. The temperature of this steam is 200C. The balance of
the steam leaves the turbine at 15kpa, 90% quality. Find the availability per kg
of steam at the entry, the isentropic efficiency and the second law efficiency of
the turbine. What is the actual work output of the turbine Ans: 1110 kj/kg,
eta_isen=.7975, eta_2nd=.8176, w_act=20144 kw
Example problem

6. m1=30 [kg/s]; m2= 5[kg/s]; m3=25 [kg/s]
p1=3000; p2=500; p3=15; x3=.9; p0=100
t1= 350; t2=200; t0=25; t0k=298
h1=enthalpy(steam,p=p1,t=t1)
s1=entropy(steam,p=p1,t=t1)
h0=enthalpy(water,p=p0,t=t0)
s0=entropy(water,p=p0,t=t0)
h2=enthalpy(steam,p=p2,t=t2)
s2=entropy(steam,p=p2,t=t2)
h3=enthalpy(steam,p=p3,x=x3)
s3=entropy(steam,p=p3,x=x3)
a1=h1-t0k*s1-(h0-t0k*s0) { availability at entry}
a2=h2-t0k*s2-(h0-t0k*s0)
a3=h3-t0k*s3-(h0-t0k*s0)
m1*h1=m2*h2+m3*h3+w3 { w3 = actual work output}
m1*s1+s_gen=m2*s2+m3*s3
w_rev=w3+t0k*s_gen
eta_2nd=w3/w_rev
h2s=enthalpy(steam,p=p2,s=s1)
h3s=enthalpy(steam,p=p3,s=s1)
m1*h1=m2*h2s+m3*h3s+w3_s {w3s = isentropic work of turbine}
eta_isen=w3/w3_s
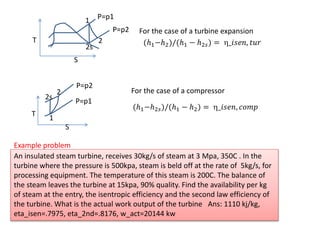
30kg/s
3MPa, 350C
5kg/s
.5MPa, 200C
25kg/s
15kPa, 90%quality
1
2
3
𝑤cv